Introdução
Este curso tem como objetivo propagar as ideias básicas de aprendizado de máquina e previsão no software estatístico R. A ideia principal é cobrir as técnicas mais usadas como regressão linear, árvores de decisão, e também detalhes básicos e aspectos práticos do aprendizado de máquina. Inicialmente será utilizado alguns códigos básicos do R para alguns modelos de previsão. Contudo, o foco principal será no pacote caret, o qual tem a finalidade de tornar as técnicas de aprendizado mais simples, combinando um grande número de preditores que foram construídos no R.
Pré-requisitos
Os pré-requisitos que serão úteis para o curso são: análise exploratória de dados no R, programação básica em R e conhecimentos teóricos básicos sobre modelos de regressão.
O que é o Aprendizado de Máquina?
Em 1959, Arthur Samuel definiu o aprendizado de máquina como o “campo de estudo que dá aos computadores a habilidade de aprender sem serem explicitamente programados”. Ou seja, é um método de análise de dados que automatiza a construção de modelos analíticos. É baseado na ideia de que sistemas podem aprender com dados, identificar padrões e tomar decisões com o mínimo de intervenção humana. A importância desse aprendizado se deve principalmente ao fato de que atualmente tem surgido cada vez mais a necessidade de manipulações de grandes volumes e variedades de dados disponíveis.
Para que serve?
Com o aprendizado de máquina é possível produzir, rápida e automaticamente, modelos capazes de analisar dados maiores e mais complexos, e entregar resultados mais rápidos e precisos – mesmo em grande escala.
Onde é usado?
Ao construir modelos precisos há mais chances de identificar boas oportunidades e de evitar riscos desconhecidos. Na prática, podemos citar alguns exemplos reais do uso de aprendizado de máquina:
- Os governos locais podem tentar prever os pagamentos de pensão no futuro para que eles saibam se seus mecanismos de geração de receita têm fundos suficientes gerados para cobrir esses pagamentos de pensão.
- O Google pode querer prever se você vai clicar em um anúncio para que ele possa mostrar apenas os anúncios com maior probabilidade de receber cliques e, assim, aumentar a receita.
- A Amazon, a Netflix e outras empresas como essa mostram um filme e querem que você veja um próximo filme. Para fazer isso, eles querem mostrar a você o que você pode estar interessado, para que eles possam mantê-lo assistindo e, novamente, aumentar a receita.
- As seguradoras empregam grandes grupos de atuários e estatísticos para tentar prever seu risco de todo tipo de coisas diferentes, como por exemplo a morte.
Como funciona?
A funcionalidade do aprendizado de máquina se resume a tentar prever um certo modelo para o conjunto de dados em questão. Há dois modos de isso ser feito: pelo aprendizado supervisionado e pelo aprendizado não supervisionado. Veremos a definição de cada um deles a seguir.
Tipos de Aprendizado de Maquina
Aprendizado não supervisionado
Na aprendizagem não supervisionada, temos um conjunto de dados não rotulados e queremos de alguma forma agrupá-los por um certo padrão encontrado. Vejamos alguns exemplos:
- Exemplo 1: Dada uma imagem de homem/mulher, temos de prever sua idade com base em dados da imagem.
- Exemplo 2: Dada as informações sobre que músicas uma pessoa costuma ouvir, sugerir outras que possam agradá-la também.
Aprendizado supervisionado
No aprendizado supervisionado, por outro lado, temos um conjunto de dados já rotulados que sabemos qual é a nossa saída correta e que deve ser semelhante ao conjunto. Queremos assim, com base nesses dados, ser capaz de classificar outros dados do mesmo tipo e que ainda não foram rotulados.
- Exemplo 1: Dada uma coleção de 1000 pesquisas de uma universidade, encontrar uma maneira de agrupar automaticamente estas pesquisas em grupos que são de alguma forma semelhantes ou relacionadas por diferentes variáveis, tais como a frequência das palavras, frases, contagem de páginas, etc.
- Exemplo 2: Dada uma grande amostra de e-mails, encontrar uma maneira de agrupá-los automaticamente em “spam” ou “não spam”, de acordo com as características das palavras, tais como a frequência com que uma certa palavra aparece, a frequência de letras maiúsculas, de cifrões ($), entre outros.
Se os valores da variável rótulo, também chamada de variável de interesse, são valores discretos finitos ou ainda categóricos, então temos um problema de classificação e o algoritmo que criaremos para resolver nosso problema será chamado Classificador.
Se os valores da Variável de Interesse são valores contínuos, então temos um problema de regressão e o algoritmo que criaremos será chamado Regressor.
A aprendizagem supervisionada será o principal foco do curso.
Predição
Queremos então construir um algoritmo “preditor” capaz de inferir se um dado pertence ou não a uma certa categoria. O preditor será formado dos seguintes componentes:
Pergunta $\rightarrow$ Amostra de entrada $\rightarrow$ Características $\rightarrow$ Algoritmo $\rightarrow$ Parâmetros $\rightarrow$ Avaliação
Pergunta
O nosso objetivo é responder a uma pergunta de tipo “O dado A é do tipo x ou do tipo y?”. Por exemplo, podemos querer saber se é possível detectar automaticamente se um e-mail é um spam ou um “ham”, isto é, não spam. O que na verdade queremos saber é: “É possível usar características quantitativas para classificar um e-mail como spam?”.
Amostra de Entrada
Uma vez formulada a pergunta, precisamos obter uma amostra de onde tentaremos extrair informações que caracterizam a categoria a qual um dado pertence e então usar essas informações para classificar outros dados não categorizados. O ideal é que se tenha uma amostra grande, assim teremos melhores parâmetros para construir nosso preditor.
No caso da pergunta sobre um e-mail ser spam ou não, temos acesso a base de dados “spam” disponível no pacote “kernlab”, onde cada linha dessa base é um e-mail e nas colunas temos a porcentagem de palavras e números contidos em cada e-mail e, entre outras coisas, a nossa variável de interesse “type” que classifica o e-mail como spam ou não:
library(kernlab)
data(spam)
head(spam)
## make address all num3d our over remove internet order mail receive will people report addresses free business email
## 1 0.00 0.64 0.64 0 0.32 0.00 0.00 0.00 0.00 0.00 0.00 0.64 0.00 0.00 0.00 0.32 0.00 1.29
## 2 0.21 0.28 0.50 0 0.14 0.28 0.21 0.07 0.00 0.94 0.21 0.79 0.65 0.21 0.14 0.14 0.07 0.28
## 3 0.06 0.00 0.71 0 1.23 0.19 0.19 0.12 0.64 0.25 0.38 0.45 0.12 0.00 1.75 0.06 0.06 1.03
## 4 0.00 0.00 0.00 0 0.63 0.00 0.31 0.63 0.31 0.63 0.31 0.31 0.31 0.00 0.00 0.31 0.00 0.00
## 5 0.00 0.00 0.00 0 0.63 0.00 0.31 0.63 0.31 0.63 0.31 0.31 0.31 0.00 0.00 0.31 0.00 0.00
## 6 0.00 0.00 0.00 0 1.85 0.00 0.00 1.85 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
## you credit your font num000 money hp hpl george num650 lab labs telnet num857 data num415 num85 technology num1999
## 1 1.93 0.00 0.96 0 0.00 0.00 0 0 0 0 0 0 0 0 0 0 0 0 0.00
## 2 3.47 0.00 1.59 0 0.43 0.43 0 0 0 0 0 0 0 0 0 0 0 0 0.07
## 3 1.36 0.32 0.51 0 1.16 0.06 0 0 0 0 0 0 0 0 0 0 0 0 0.00
## 4 3.18 0.00 0.31 0 0.00 0.00 0 0 0 0 0 0 0 0 0 0 0 0 0.00
## 5 3.18 0.00 0.31 0 0.00 0.00 0 0 0 0 0 0 0 0 0 0 0 0 0.00
## 6 0.00 0.00 0.00 0 0.00 0.00 0 0 0 0 0 0 0 0 0 0 0 0 0.00
## parts pm direct cs meeting original project re edu table conference charSemicolon charRoundbracket
## 1 0 0 0.00 0 0 0.00 0 0.00 0.00 0 0 0.00 0.000
## 2 0 0 0.00 0 0 0.00 0 0.00 0.00 0 0 0.00 0.132
## 3 0 0 0.06 0 0 0.12 0 0.06 0.06 0 0 0.01 0.143
## 4 0 0 0.00 0 0 0.00 0 0.00 0.00 0 0 0.00 0.137
## 5 0 0 0.00 0 0 0.00 0 0.00 0.00 0 0 0.00 0.135
## 6 0 0 0.00 0 0 0.00 0 0.00 0.00 0 0 0.00 0.223
## charSquarebracket charExclamation charDollar charHash capitalAve capitalLong capitalTotal type
## 1 0 0.778 0.000 0.000 3.756 61 278 spam
## 2 0 0.372 0.180 0.048 5.114 101 1028 spam
## 3 0 0.276 0.184 0.010 9.821 485 2259 spam
## 4 0 0.137 0.000 0.000 3.537 40 191 spam
## 5 0 0.135 0.000 0.000 3.537 40 191 spam
## 6 0 0.000 0.000 0.000 3.000 15 54 spam
Obtida a amostra, precisamos dividi-la em duas partes que chamaremos de Conjunto de Treino e Conjunto de Teste. O conjunto de treino será usado para construir o algoritmo. É dele que vamos extrair as informações que julgarmos utéis para classificar uma categoria de dado. É importante que o modelo de previsão seja feito com base apenas no conjunto de treino.
set.seed(127)
indices = sample(dim(spam)[1], size = 2760)
treino = spam[indices,]
teste = spam[-indices,]
Após construido o algoritmo, usaremos o conjunto de teste para obter a estimativa de erro, que será detalhada mais a frente.
Características
Temos que encontrar agora características que possam indicar a categoria dos dados. Podemos, por exemplo, vizualizar algumas variáveis graficamente para obter uma ideia do que podemos fazer. No nosso exemplo de e-mails, podemos querer avaliar se a frequência de palavras “your” em um e-mail pode indicar se ele é um spam ou não.
plot(density(treino$your[treino$type=="nonspam"]), col="blue",
main = "Densidade de 'your' em ham (azul) e spam (vermelho)",
xlab = "Frequência de 'your'", ylab = "densidade")
lines(density(treino$your[treino$type=="spam"]), col="red")
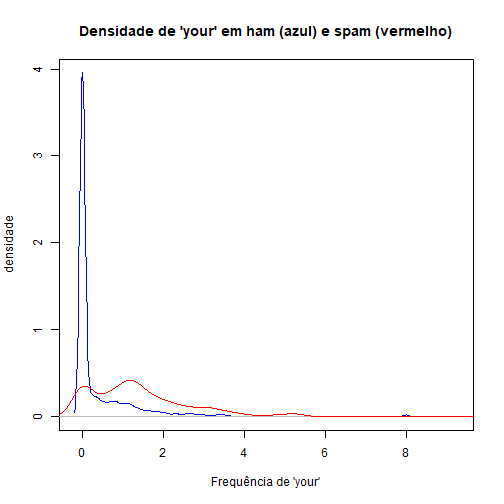
Pelo gráfico podemos notar que a maioria dos e-mails que são spam têm uma frequência maior da palavra “your”. Por outro lado, aqueles que são classificados como ham (não spam) têm um pico mais alto perto do 0.
Algoritmo
Com base nisso podemos construir um algoritmo para prever se um e-mail é spam ou ham. Podemos estimar um modelo onde queremos encontrar uma constante c tal que se a frequência da palavra “your” for maior que c, então classificamos o e-mail como spam. Caso contrário, classificamos o e-mail como não spam.
Vamos observar graficamente como ficaria esse modelo se c=0.8.
plot(density(treino$your[treino$type=="nonspam"]), col="blue",
main = "Densidade de 'your' em ham (azul) e spam (vermelho)",
xlab = "Frequência de 'your'", ylab = "densidade")
lines(density(treino$your[treino$type=="spam"]), col="red")
abline(v=0.8,col="black")
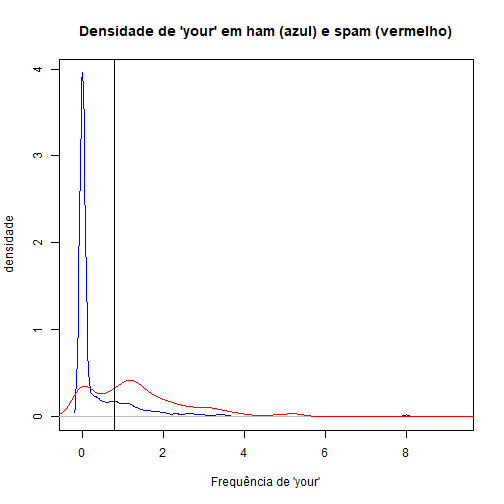
Os e-mails à direita da linha preta seriam classificados como spam, enquanto que os à esquerda seriam classificados como não spam.
Avaliação
Agora vamos avaliar nosso modelo de predição.
predicao=ifelse(treino$your>0.8,"spam","nonspam")
table(predicao,treino$type)/length(treino$type)
##
## predicao nonspam spam
## nonspam 0.4978261 0.1293478
## spam 0.1155797 0.2572464
Podemos ver que quando os e-mails não eram spam e classificamos como “não spam”, de acordo com nosso modelo, em 50% do tempo nós acertamos. Quando os e-mails eram spam e classificamos ele em spam, por volta de 26% do tempo nós acertamos. Então, ao total, nós acertamos por volta de 50+26=76% do tempo. Então nosso algoritmo de previsão tem uma precisão por volta de 76% na amostra treino.
predicao=ifelse(teste$your>0.8,"spam","nonspam")
table(predicao,teste$type)/length(teste$type)
##
## predicao nonspam spam
## nonspam 0.4910375 0.1434003
## spam 0.1037480 0.2618142
Já na amostra teste acertamos 48+27=75% das vezes. O erro na amostra teste é o que chamamos de erro real. É o erro que esperamos em amostras novas que passarem por nosso preditor.
Como construir um bom algoritmo de aprendizado de máquina?
O “melhor” método de aprendizado de máquina é caracterizado por:
- Uma boa base de dados;
- Reter informações relevantes;
- Ser bem interpretável;
- Fácil de ser explicado e entendido;
- Ser preciso;
- Fácil de se construir e de se testar em pequenas amostras;
- Fácil aplicar a um grande conjunto de dados.
Os erros mais comuns, que se deve tomar um certo cuidado, são:
- Tentar automatizar a seleção de variáveis (características) de uma maneira que não permita que você entenda como essas variáveis estão sendo aplicadas para fazer previsões;
- Não prestar atenção a peculiaridades específicas de alguns dados, como comportamentos estranhos de variáveis específicas;
- Jogar fora informações desnecessariamente.
Design de predição
1. Defina sua taxa de erro (benchmark).
Por hora iremos utilizar uma taxa de erro genérica, mas em um próximo iremos falar sobre quais são as diferentes taxas de erro possíveis que você pode escolher.
Por exemplo, podemos calcular o chamado erro majoritário que é o limite máximo abaixo do qual o erro de um classificador deve estar. Ele é dado por $1-p$, onde $p$ é a proporção da categoria mais requente na variável de interesse. Por exemplo, se a variável de interesse possui 2 categorias: A e B. Se $85\%$ dos dados estão rotulados na categoria A e $15\%$ na categoria B, entao temos que a categoria A é a classe majoritária e $100\%-85\% = 15\%$ é o erro majoritário.
Caso o erro do preditor seja superior ao erro majoritário, seria melhor classificar toda nova amostra na classe majoritária, certo? Depende.
Digamos que um psicólogo quer construir um classificador para prever se uma pessoa tem ou não indeação suicida, ou seja, pensa ou planeja suicídio. Suponha que ele tem uma base de dados com 1000 observações cuja variável de interesse “Tem indeação suicida?” está rotulada com “sim” ou “não” e 97% das observações, no caso indivíduos/pacientes, não possuem tal característica e portanto 3% dos indivíduos possuem. Criado o preditor, observamos que o erro é de 5%, assim como mostrado a seguir:
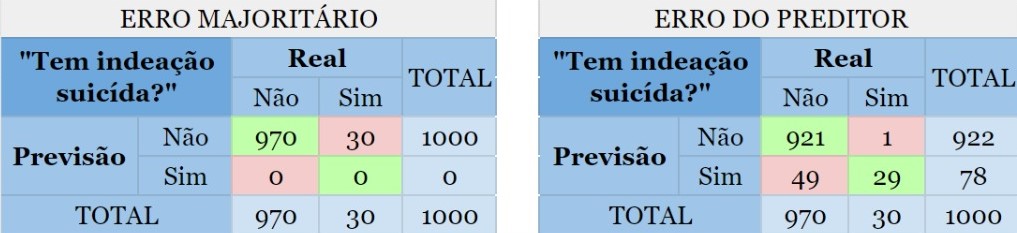
As partes em vermelho mostram o erro cometido por ambos os métodos. Agora note as pessoas que possuem indeação suicída porém foram classficadas como não possuidoras dessa característica. Quanto isso afetará no dignóstico do psicólogo?
2. Divida os dados em Treino e Teste, ou Treino, Teste e Validação (opcional).
Como já comentado, o conjunto de treino deve ser criado para construir seu modelo e o conjunto de testes para avaliar seu modelo. Fazemos isso com o intuito de criarmos um modelo que se ajuste bem a qualquer base de dados, e não apenas à nossa. É comum usar 70% da amostra como treino e 30% como teste, mas isso não é uma regra. Podemos também repartir os dados em treino, teste e validação(*). É importante ficar claro que quem está conduzindo as análises é quem fica encarregado de decidir o que fica melhor para cada amostra.
3. Definimos quais variáveis serão utilizadas para estimação dos parâmetros do classificador/regressor (função preditora).
Nem sempre utilizar todas as variáveis do banco de dados é importante para o modelo. Pode acontecer de termos variáveis que não ajudam na predição, como por exemplo aquelas com uma variância quase zero (frequência muito alta de um único valor). Iremos estudar algumas formas de selecionar as melhores variáveis para o modelo em breve.
4. Definimos o método que será utilizado para construção do classificador/regressor.
Isso poderá ser feito, por exemplo, utilizando o método de validação cruzada (cross-validation), que será explicado detalhadamente em um capítulo mais à frente.
5. Utilizando a amostra TREINO, definimos os parâmetros da função preditora (classificador/regressor), obtendo o melhor modelo possível.
6. Aplicamos o melhor modelo obtido na amostra TESTE uma única vez, para estimar o erro do preditor.
Aplicamos o melhor modelo na amostra teste apenas uma vez porque se aplicarmos diversas vezes até achar o melhor modelo estaremos utilizando o teste, de certa forma, para treinar o modelo, pois o ajuste do modelo seria influenciado pelo resultado do teste. Isso não é desejável pois o objetivo do teste é nos servir como uma “nova amostra”.
(*) Opcionalmente poderá ser criado um conjunto de validação, com o intuito de servir como um “pré-teste”, que também será usado para avaliar seu modelo. Quando repartimos o conjunto de dados dessa forma, utilizamos o treino para construir o modelo, avaliamos o modelo na validação (ou seja, o ajuste do modelo é influenciado por ela), e se o resultado não for bom, retornamos ao treino para ajustar um outro modelo. Então novamente testamos o modelo na validação, e assim sucessivamente até acharmos um modelo que se adequou bem tanto ao treino quanto à validação. Aí, finalmente, aplicamos ele ao conjunto teste, avaliando na prática a sua qualidade.
Erros Amostrais
Este é um dos conceitos mais fundamentais com os quais lidamos na aprendizagem de máquina e previsão. Temos duas taxas de erros amostrais: o erro dentro da amostra (in sample error) e o erro fora da amostra (out of sample error).
Erro dentro da Amostra (In Sample Error)
É a taxa de erro que você recebe no mesmo conjunto de dados usado para criar seu preditor. Na literatura às vezes é chamado de erro de resubstituição. Em outras palavras, é quando seu algoritmo de previsão se ajusta ao que você coletou num conjunto de dados específico. E assim, quando você recebe um novo conjunto de dados, a precisão diminuirá.
Erro fora da Amostra (Out of Sample Error)
É a taxa de erro que você recebe em um novo conjunto de dados. Na literatura às vezes é chamado de erro de generalização. Uma vez que coletamos uma amostra de dados e construímos um modelo para ela, podemos querer testá-lo em uma nova amostra, por exemplo uma amostra coletada em um horário diferente ou em um local diferente. Daí podemos analisar o quão bem o algoritmo executará a predição nesse novo conjunto de dados.
Algumas ideias-chave
- Quase sempre o erro fora da amostra é o que interessa.
- Erro dentro da amostra é menor que o erro fora da amostra.
- Um erro frequente é ajustar muito o algoritmo aos dados que temos. Em outras palavras, criar um modelo overfitting(*).
(*) Overfitting é um termo usado na estatística para descrever quando um modelo estatístico se ajusta muito bem a um conjunto de dados anteriormente observado e, como consequência, se mostra ineficaz para prever novos resultados.
Vejamos um exemplo de erro dentro da amostra vs erro fora da amostra:
set.seed(131)
# Vamos selecionar as linhas da base de dados spam através de uma amostra de tamanho 10 das 4601 linhas
# dos dados:
spamMenor = spam[sample(dim(spam)[1], size = 10), ]
# Vamos criar um vetor composto pelos rótulos "1" e "2".
# Se um e-mail da nossa amostra for spam, recebe "1", se não for spam, recebe "2".
spamRotulos = (spamMenor$type == "spam")*1 + 1
# Na nossa base a variável capitalAve representa a média de letras maiúsculas por linha.
plot(spamMenor$capitalAve, col = spamRotulos, xlab = "Quantidade de Letras Maiúsculas",
ylab = "Frequência", main = "Letras Maiúsculas em spam (vermelho) e em ham (preto)",
pch = 19)
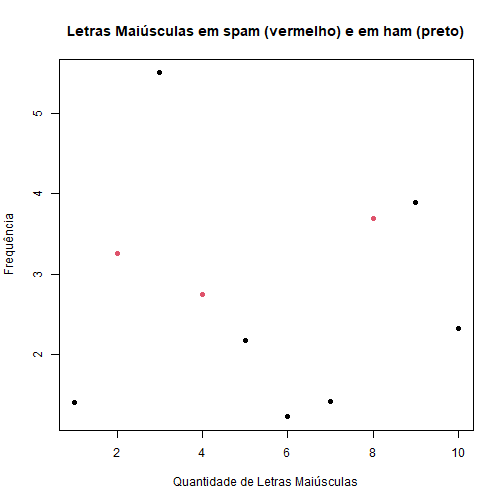
Podemos notar que, em geral, as mensagens classificadas como spam possuem uma frequência maior de letras maiúsculas do que as mensagens classificadas como não spam. Com base nisso queremos construir um preditor, onde podemos classificar e-mails como spam se a frequência de letras maiúsculas for maior que uma determida constante, e não spam caso contrário.
Veja que se separarmos os dados pela frequência de letras maiúsculas maior que 2,5 e classificarmos o que está acima como spam e abaixo como não spam, ainda teríamos duas observações que não são spam acima da linha.
plot(spamMenor$capitalAve, col = spamRotulos, xlab = "Quantidade de Letras Maiúsculas",
ylab = "Frequência", main = "Letras Maiúsculas em spam (vermelho) e em ham (preto)",
pch = 19)
abline(h = 2.5, lty = 3, col = "blue")
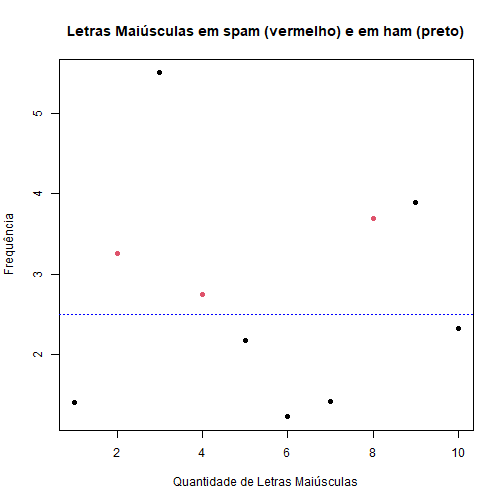
Então o melhor para esse caso é criar o seguinte modelo:
- letras maiúsculas > 2,5 e < 3,8 $\Rightarrow$ spam;
- letras maiúsculas < 2,5 ou > 3,8 $\Rightarrow$ não spam.
plot(spamMenor$capitalAve, col = spamRotulos, xlab = "Quantidade de Letras Maiúsculas",
ylab = "Frequência", main = "Letras Maiúsculas em spam (vermelho) e em ham (preto)",
pch = 19)
abline(h = c(2.5, 3.8), lty = 3, col = "blue")
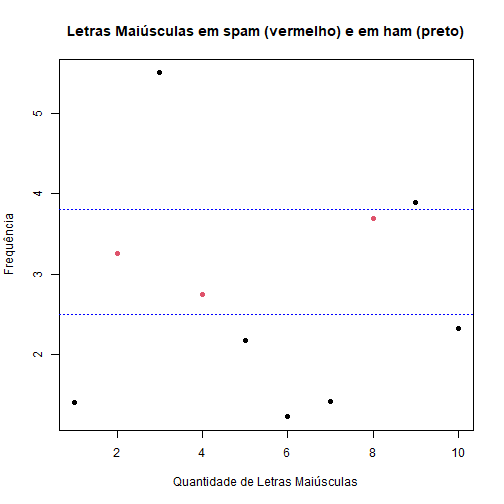
# construindo o modelo sobreajustado
modelo.sobreajustado = function(x){
predicao = rep(NA, length(x))
predicao[(x>=2.5 & x<=3.8)] = "spam"
predicao[(x<2.5 | x>3.8)] = "nonspam"
return(predicao)
}
# avaliando o modelo sobreajustado
resultado = modelo.sobreajustado(spamMenor$capitalAve)
table(resultado, spamMenor$type)
##
## resultado nonspam spam
## nonspam 7 0
## spam 0 3
Note que obtivemos uma precisão perfeita nessa amostra, como já era esperado. Nesse caso, o erro dentro da amostra é de 0%. Mas será que esse modelo é o mais eficiente em outros dados também?
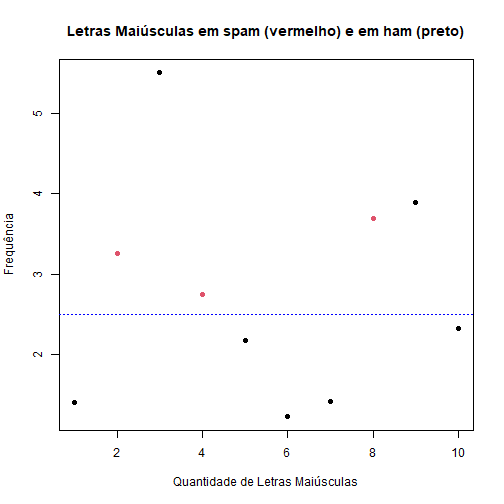
Vamos usar essa segunda regra para criarmos um modelo mais geral:
- letras maiúsculas > 2,5 $\Rightarrow$ spam;
- letras maiúsculas <= 2,5 $\Rightarrow$ não spam.
plot(spamMenor$capitalAve, col = spamRotulos, xlab = "Quantidade de Letras Maiúsculas",
ylab = "Frequência", main = "Letras Maiúsculas em spam (vermelho) e em ham (preto)",
pch = 19)
abline(h = 2.5, lty = 3, col = "blue")
# construindo o modelo geral
modelo.geral = function(x){
predicao = rep(NA, length(x))
predicao[x>=2.5] = "spam"
predicao[x<2.5] = "nonspam"
return(predicao)
}
# avaliando o modelo geral
resultado2 = modelo.geral(spamMenor$capitalAve)
table(resultado2, spamMenor$type)
##
## resultado2 nonspam spam
## nonspam 5 0
## spam 2 3
Observe que dessa forma temos um erro dentro da amostra de 20%. Vamos agora aplicar esses dois modelos para toda a base de dados:
table(modelo.sobreajustado(spam$capitalAve), spam$type)
##
## nonspam spam
## nonspam 2297 1385
## spam 491 428
table(modelo.geral(spam$capitalAve), spam$type)
##
## nonspam spam
## nonspam 2042 540
## spam 746 1273
Olhando para a precisão de nossos modelos:
sum(modelo.sobreajustado(spam$capitalAve) == spam$type)
## [1] 2725
sum(modelo.geral(spam$capitalAve) == spam$type)
## [1] 3315
Observe que utilizando o modelo sobreajustado obtivemos um erro fora da amostra de 40,77%, enquanto que com o modelo geral esse erro foi de 27,95%. Note que se queremos construir um modelo que melhor representa qualquer amostra que pegarmos, um modelo não sobreajustado possuirá uma precisão maior.
Avaliando Preditores - Introdução ao Pacote Caret
O pacote caret (abreviação de Classification And Regression Training) é um pacote muito útil para o machine learning pois envolve algoritmos que possibilitam que as previsões sejam feitas de forma mais prática, simplificando o processo de criação de modelos preditivos. Neste guia detalhado pode ser encontrado mais informações sobre o pacote.
Avaliando Classificadores
Vamos utilizar a base de dados spam novamente para realizarmos o procedimento de predição para um e-mail (se ele é spam ou não spam), dessa vez utilizando o pacote caret.
Para fazer a separação da amostra em treino e teste vamos primeiramente particionar a base de dados com a função createDataPartition().
library(caret)
library(kernlab)
data(spam)
set.seed(371)
noTreino = createDataPartition(y = spam$type, p = 0.75, list = F)
Essa função retorna os números das linhas a serem selecionadas para o treino. Os principais argumentos são:
- y = classe dos dados que deverá ser mantida a mesma proporção nos conjuntos treino e teste. Para o nosso exemplo, escolhemos manter a mesma proporção do tipo do e-mail. Sendo assim, tanto no treino como no teste teremos a mesma proporção de e-mails spam e não spam.
- p = porcentagem da amostra que será utilizada para o treino. Para o nosso exemplo, escolhemos 75%.
- list = argumento do tipo logical, se TRUE $\rightarrow$ os resultados serão mostrados em uma lista, se FALSE $\rightarrow$ os resultados serão mostrados em uma matriz.
OBS: Esse comando deve ser utilizado apenas quando os dados são amostras independentes.
Agora vamos separar o que irá para o treino e o que irá para o teste.
# Separando as linhas para o treino:
treino = spam[noTreino,]
# Separando as linhas para o teste:
teste = spam[-noTreino,]
Dado que já foi feito a separação das amostras treino e teste, o próximo passo é realizarmos o treinamento. Para isso é preciso escolher um dos modelos para ser utilizado. Uma lista com todos os modelos implementados no pacote caret pode ser vista com o seguinte comando:
names(getModelInfo())
## [1] "ada" "AdaBag" "AdaBoost.M1" "adaboost" "amdai"
## [6] "ANFIS" "avNNet" "awnb" "awtan" "bag"
## [11] "bagEarth" "bagEarthGCV" "bagFDA" "bagFDAGCV" "bam"
## [16] "bartMachine" "bayesglm" "binda" "blackboost" "blasso"
## [21] "blassoAveraged" "bridge" "brnn" "BstLm" "bstSm"
## [26] "bstTree" "C5.0" "C5.0Cost" "C5.0Rules" "C5.0Tree"
## [31] "cforest" "chaid" "CSimca" "ctree" "ctree2"
## [36] "cubist" "dda" "deepboost" "DENFIS" "dnn"
## [41] "dwdLinear" "dwdPoly" "dwdRadial" "earth" "elm"
## [46] "enet" "evtree" "extraTrees" "fda" "FH.GBML"
## [51] "FIR.DM" "foba" "FRBCS.CHI" "FRBCS.W" "FS.HGD"
## [56] "gam" "gamboost" "gamLoess" "gamSpline" "gaussprLinear"
## [61] "gaussprPoly" "gaussprRadial" "gbm_h2o" "gbm" "gcvEarth"
## [66] "GFS.FR.MOGUL" "GFS.LT.RS" "GFS.THRIFT" "glm.nb" "glm"
## [71] "glmboost" "glmnet_h2o" "glmnet" "glmStepAIC" "gpls"
## [76] "hda" "hdda" "hdrda" "HYFIS" "icr"
## [81] "J48" "JRip" "kernelpls" "kknn" "knn"
## [86] "krlsPoly" "krlsRadial" "lars" "lars2" "lasso"
## [91] "lda" "lda2" "leapBackward" "leapForward" "leapSeq"
## [96] "Linda" "lm" "lmStepAIC" "LMT" "loclda"
## [101] "logicBag" "LogitBoost" "logreg" "lssvmLinear" "lssvmPoly"
## [106] "lssvmRadial" "lvq" "M5" "M5Rules" "manb"
## [111] "mda" "Mlda" "mlp" "mlpKerasDecay" "mlpKerasDecayCost"
## [116] "mlpKerasDropout" "mlpKerasDropoutCost" "mlpML" "mlpSGD" "mlpWeightDecay"
## [121] "mlpWeightDecayML" "monmlp" "msaenet" "multinom" "mxnet"
## [126] "mxnetAdam" "naive_bayes" "nb" "nbDiscrete" "nbSearch"
## [131] "neuralnet" "nnet" "nnls" "nodeHarvest" "null"
## [136] "OneR" "ordinalNet" "ordinalRF" "ORFlog" "ORFpls"
## [141] "ORFridge" "ORFsvm" "ownn" "pam" "parRF"
## [146] "PART" "partDSA" "pcaNNet" "pcr" "pda"
## [151] "pda2" "penalized" "PenalizedLDA" "plr" "pls"
## [156] "plsRglm" "polr" "ppr" "PRIM" "protoclass"
## [161] "qda" "QdaCov" "qrf" "qrnn" "randomGLM"
## [166] "ranger" "rbf" "rbfDDA" "Rborist" "rda"
## [171] "regLogistic" "relaxo" "rf" "rFerns" "RFlda"
## [176] "rfRules" "ridge" "rlda" "rlm" "rmda"
## [181] "rocc" "rotationForest" "rotationForestCp" "rpart" "rpart1SE"
## [186] "rpart2" "rpartCost" "rpartScore" "rqlasso" "rqnc"
## [191] "RRF" "RRFglobal" "rrlda" "RSimca" "rvmLinear"
## [196] "rvmPoly" "rvmRadial" "SBC" "sda" "sdwd"
## [201] "simpls" "SLAVE" "slda" "smda" "snn"
## [206] "sparseLDA" "spikeslab" "spls" "stepLDA" "stepQDA"
## [211] "superpc" "svmBoundrangeString" "svmExpoString" "svmLinear" "svmLinear2"
## [216] "svmLinear3" "svmLinearWeights" "svmLinearWeights2" "svmPoly" "svmRadial"
## [221] "svmRadialCost" "svmRadialSigma" "svmRadialWeights" "svmSpectrumString" "tan"
## [226] "tanSearch" "treebag" "vbmpRadial" "vglmAdjCat" "vglmContRatio"
## [231] "vglmCumulative" "widekernelpls" "WM" "wsrf" "xgbDART"
## [236] "xgbLinear" "xgbTree" "xyf"
Para o nosso exemplo vamos utilizar o “glm” (generalized linear model).
Agora vamos criar o nosso modelo, utilizando apenas a amostra treino. Para isso vamos usar o comando train().
modelo = train(type ~ ., data = treino, method = "glm")
No primeiro argumento colocamos qual variável estamos tentando prever em função de qual(is). No nosso caso, queremos prever “type” em função (“~”) de todas as outras, por isso utilizamos o “.”. Em seguida dizemos de qual base de dados queremos construir o modelo e por último o método de treinamento utilizado.
Agora vamos dar uma olhada no nosso modelo.
modelo
## Generalized Linear Model
##
## 3451 samples
## 57 predictor
## 2 classes: 'nonspam', 'spam'
##
## No pre-processing
## Resampling: Bootstrapped (25 reps)
## Summary of sample sizes: 3451, 3451, 3451, 3451, 3451, 3451, ...
## Resampling results:
##
## Accuracy Kappa
## 0.9224544 0.8365594
Podemos observar que utilizamos uma amostra de tamanho 3451 no treino e 57 preditores para prever a qual classe um e-mail pertence, spam ou não spam. O que a função faz é realizar várias maneiras diferentes de testar se esse modelo funcionará bem e usar isso para selecionar o melhor modelo. Neste caso ela usou a reamostragem por bootstrapping com 25 replicações (o default da função).
Uma vez que ajustamos o modelo podemos aplicá-lo na amostra teste, para estimarmos a precisão do classificador. Para isso utilizamos o comando predict(). Dentro da função nós passamos o modelo que ajustamos no treino e em qual base de dados gostaríamos de realizar a predição.
predicao = predict(modelo, newdata = teste)
head(predicao, n=30)
## [1] spam spam spam spam spam spam spam nonspam nonspam spam spam spam nonspam nonspam
## [15] spam spam spam spam spam spam spam spam spam spam spam spam spam spam
## [29] spam spam
## Levels: nonspam spam
Ao fazermos isso obtemos uma série de predições para as classes dos e-mails do conjunto teste. Podemos então realizar a avaliação do modelo comparando os resultados da predição com as reais classes dos e-mails, por meio do comando confusionMatrix().
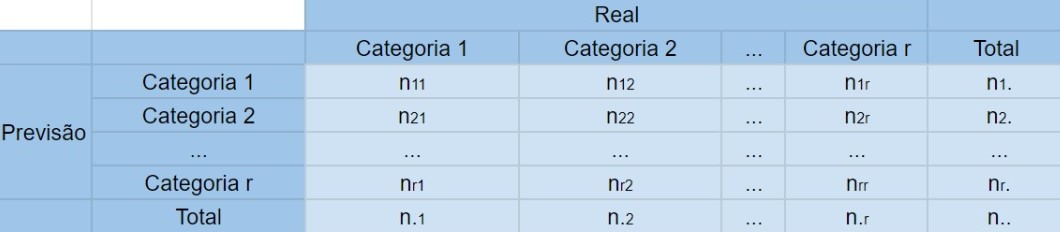
Matriz de Confusão (Confusion Matrix)
A matriz de confusão é a matriz de comparação feita após a predição, onde as linhas correspondem ao que foi previsto e as colunas correspondem à verdade conhecida.
Exemplo: A matriz de confusão para o problema de predição dos e-mails em spam ou não spam fica da seguinta forma:
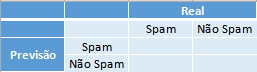
Onde na primeira coluna se encontram os elementos que possuem a característica de interesse (os e-mails que são spam), e, respectivamente nas linhas, os que foram corretamente identificados - o qual são chamados de Verdadeiros Positivos (VP) - e os que foram erroneamente identificados - os Falsos Negativos (FP). Na segunda coluna se encontram os elementos que não possuem a característica de interesse (os e-mails que são ham) e, respectivamente nas linhas, os que foram erroneamente identificados - o qual são chamados de Falsos Positivos (FN) - e os que foram corretamente identificados - os Verdadeiros Negativos (VN).
Com as devidas classificações a matriz de confusão fica da seguinte forma:
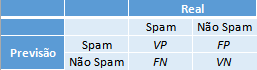
Dentro da função passamos as predições que obtemos pelo modelo ajustado e as reais classificações dos e-mails do conjunto teste.
confusionMatrix(predicao, teste$type)
## Confusion Matrix and Statistics
##
## Reference
## Prediction nonspam spam
## nonspam 659 55
## spam 38 398
##
## Accuracy : 0.9191
## 95% CI : (0.9018, 0.9342)
## No Information Rate : 0.6061
## P-Value [Acc > NIR] : < 0.0000000000000002
##
## Kappa : 0.8295
##
## Mcnemar's Test P-Value : 0.09709
##
## Sensitivity : 0.9455
## Specificity : 0.8786
## Pos Pred Value : 0.9230
## Neg Pred Value : 0.9128
## Prevalence : 0.6061
## Detection Rate : 0.5730
## Detection Prevalence : 0.6209
## Balanced Accuracy : 0.9120
##
## 'Positive' Class : nonspam
##
A função retorna a matriz de confusão e alguns dados estatísticos, como por exemplo a Precisão (Accuracy), o Intervalo de Confiança com 95% de confiança (95% CI), a Sensibilidade (Sensitivity), Especificidade (Specificity), entre outros.
Podemos notar que o GLM foi um bom modelo de treinamento para os nossos dados pois obtivemos altas taxas de acertos: uma precisão de 0,94, 0,96 de sensitividade e 0,90 de especificidade. Vamos ver melhor algumas dessas estatísticas:
Definição (Sensibilidade): A sensibilidade de um método de predição é a porcentagem dos elementos da amostra que possuem a característica de interesse e foram corretamente identificados. Para o nosso exemplo dos e-mails, a sensabilidade é a porcentagem dos e-mails que são spam e foram classificados pelo nosso algoritmo de predição como spam.
Ou seja, podemos escrever \(Sensibilidade = \frac{VP}{VP+FN}\)
Definição (Especificidade): A especificidade de um método de predição é a porcentagem dos elementos da amostra que não possuem a característica de interesse e foram corretamente identificados. Para o nosso exemplo dos e-mails, a especificidade é a porcentagem dos e-mails que são “ham” e o algoritmo de predição os classificou como tal.
Ou seja, podemos escrever \(Especificidade=\frac{VN}{VN+FP}\)
Quando obtemos as sensibilidades e as especificidades de diferentes preditores, naturalmente surge o questionamente: qual deles é melhor para estimar as verdadeiras características de interesse? A resposta depende do que é mais importante para o problema.
Se identificar corretamente os positivos for mais importante, utilizamos o preditor com maior sensibilidade. Se identificar corretamente os negativos for mais importante, utilizamos o preditor com maior especificidade.
Outra medida para avaliar a qualidade do nosso preditor é a precisão (Accuracy). Ela avalia a porcentagem de acertos que tivemos em geral. Ou seja, somamos o número de Verdadeiros Positivos com o número de Verdadeiros Negativos e dividimos pelo tamanho da amostra. \(Precisão=\frac{VP+VN}{VP+VN+FN+FP}\)
Para demais medidas da matriz de confusão consulte o [apêndice].
Avaliando Regressores
Agora vamos utilizar a base de dados faithful para tentar prever o tempo de espera (waiting) entre uma erupção e outra de um gêiser dado a duração das erupções (eruption).
data("faithful")
head(faithful)
## eruptions waiting
## 1 3.600 79
## 2 1.800 54
## 3 3.333 74
## 4 2.283 62
## 5 4.533 85
## 6 2.883 55
Primeiro, vamos separar a amostra em treino e teste.
set.seed(39)
noTreino = createDataPartition(y=faithful$waiting, p=0.7, groups = 5, list=F)
treino = faithful[noTreino,]; teste = faithful[-noTreino,]
Quando o argumento y é numérico, a amostra é dividida em grupos com base nos percentis e é feita uma amostragem estratificada. O número de percentis é definido pelo argumento groups.
Agora temos que treinar nosso modelo. Para esse exemplo vamos usar a Regressão Linear (LM - Linear Regression).
Os métodos disponíveis e seus usos podem ser encontrados no guia do caret.
Vamos treinar nosso modelo utilizando a amostra treino.
modelo = caret::train(waiting~eruptions, data = treino, method = "lm")
Novamente, colocamos a variável que tentamos prever em função das outras. No caso, só temos duas variáveis então não precisamos colocar o ponto como no [classificador].
modelo
## Linear Regression
##
## 192 samples
## 1 predictor
##
## No pre-processing
## Resampling: Bootstrapped (25 reps)
## Summary of sample sizes: 192, 192, 192, 192, 192, 192, ...
## Resampling results:
##
## RMSE Rsquared MAE
## 6.060639 0.805468 4.948071
##
## Tuning parameter 'intercept' was held constant at a value of TRUE
Podemos ver que temos 192 observações no conjunto treino e 1 preditor.
Agora vamos aplicar nosso modelo na amostra teste para avaliar o erro dele.
predicao = predict(modelo, newdata = teste)
Assim como no classificador, a função predict nos retorna a previsão dos tempos entre as erupções dado os tempos das durações das erupções.
MSE
Assim como há diversas formas de compararmos a qualidade dos classificadores, há também diversas formas de compararmos regressores. O que estudaremos agora é o MSE (mean squared error - erro quadrático médio). Mais formas de comparação de regressores também serão vistas futuramente.
O MSE é a média de quanto os valores previstos para as observações se distanciaram dos valores verdadeiros dessa observação. Obtemos ele somando essas distâncias entre os valores previstos e os reais ao quadrado e dividindo por n.
\[MSE=\frac{1}{n} \sum\limits_{i=1}^{n} \left( Yreal_i-Yestimado_i \right)^{2}\]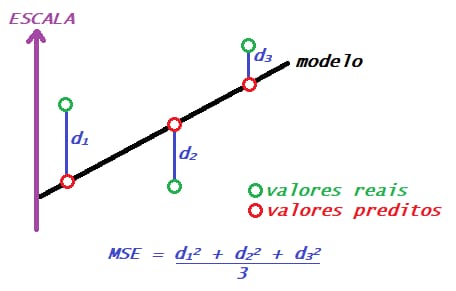
Ex.: O erro quadrático médio para o problema de tempo de erupção do gêiser.
data("faithful")
head(faithful)
## eruptions waiting
## 1 3.600 79
## 2 1.800 54
## 3 3.333 74
## 4 2.283 62
## 5 4.533 85
## 6 2.883 55
# Gráfico do tempo entre as erupções em função do tempo de erupção do gêiseres
plot(faithful$eruptions, faithful$waiting, pch = 20, ylab="Tempo entre Erupções",
xlab = "Tempo de Erupção", main = "Tempo entre as erupções em função do tempo de erupção do gêiser")
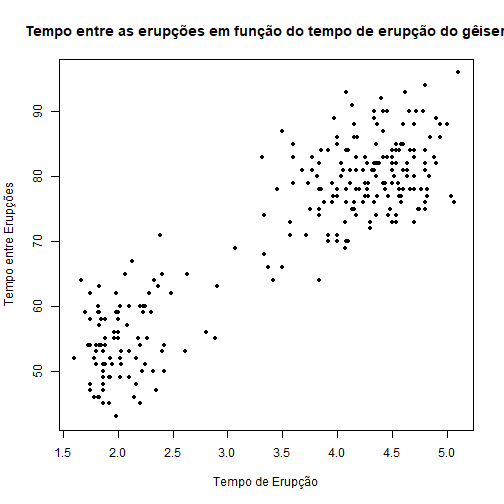
Podemos notar que há uma relação linear positiva entre as variáveis. Vamos então ajustar um modelo de regressão linear.
modelo = lm(faithful$waiting~faithful$eruptions)
plot(y = faithful$waiting, x = faithful$eruptions, pch = 20, ylab="Tempo entre erupções",
xlab = "Tempo de erupção", main = "Tempo entre as erupções em função do tempo de erupção do gêiser")
abline(modelo, col = "red", lwd = 2)
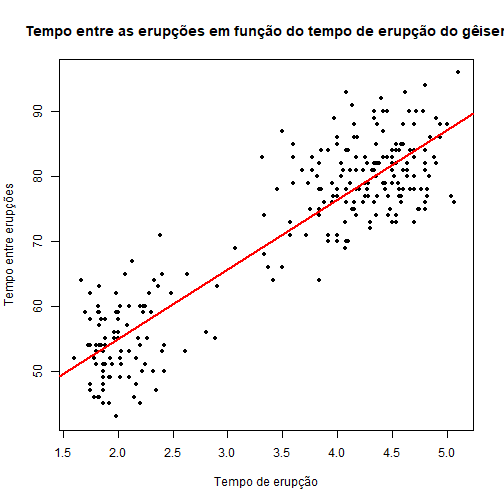
Na reta de regressão temos todos os valores previstos para o tempo de erupção de acordo com os tempos de espera. Podemos então calcular o MSE para o nosso modelo utilizando o comando mse().
mse = sum((teste$waiting-predicao)**2)/nrow(teste)
mse
## [1] 32.41941
Então temos que, em média, o valor estimado para a variável de interesse no conjunto de teste se distancia do valor real observado em 32,41941 escores. Note que esta é uma medida que soma as distâncias ao quadrado, por isso o MSE é um número relativamente grande.
Cross Validation (Validação Cruzada)
Existem diversos métodos de aprendizado de máquina que podemos usar para construir um preditor. Então como saber qual método é melhor? Um jeito de fazer isso é usando a validação cruzada.
A Validação Cruzada nos permite comparar diferentes métodos de aprendizado de máquina ou parâmetros para o método escolhido e avaliar qual funcionará melhor na prática.
Então o que vamos fazer é, para cada método,
- Separar os dados em conjunto de treino e conjunto de teste.
- Treinar um modelo no conjunto de treino.
- Avaliar no conjunto de teste
- Repetir os passos 1-3 e estimar o erro.
Bem, já sabemos que não é uma boa ideia usar toda a base de dados para treinar o nosso preditor e então podemos dividir por exemplo os primeiros 75% dos dados para treino e 25% finais para teste. Mas, e se esse não for o melhor jeito de dividir nossos dados? E se o melhor jeito de fazer essa divisão for usando os primeiros 25% para teste e o restante para treino? A Validação cruzada leva em consideração todas essas divisões usando uma de cada vez e tirando a média dos resultados no final. Para isso veremos como realizar alguns métodos de reamostragem, para utilizarmos várias amostras possíveis e não ficarmos dependentes de uma única amostra.
Alguns Métodos de Reamostragem
Agora vamos compreender como fatiar os dados para realizarmos a reamostragem. Existem vários métodos possíveis mas vamos nos focar em três: k-fold, repeated k-fold e bootstrap.
K-fold
Este método consiste em fatiar os dados em k pedaços iguais. Utilizamos um pedaço para o teste e os demais para o treino. Então realizamos esse procedimento k vezes, de modo que em cada repetição um novo pedaço seja utilizado para o teste. Para avaliar o erro nós tiramos a média de todos os erros de todas as replicações.
Exemplo: K-fold com 10 partes:
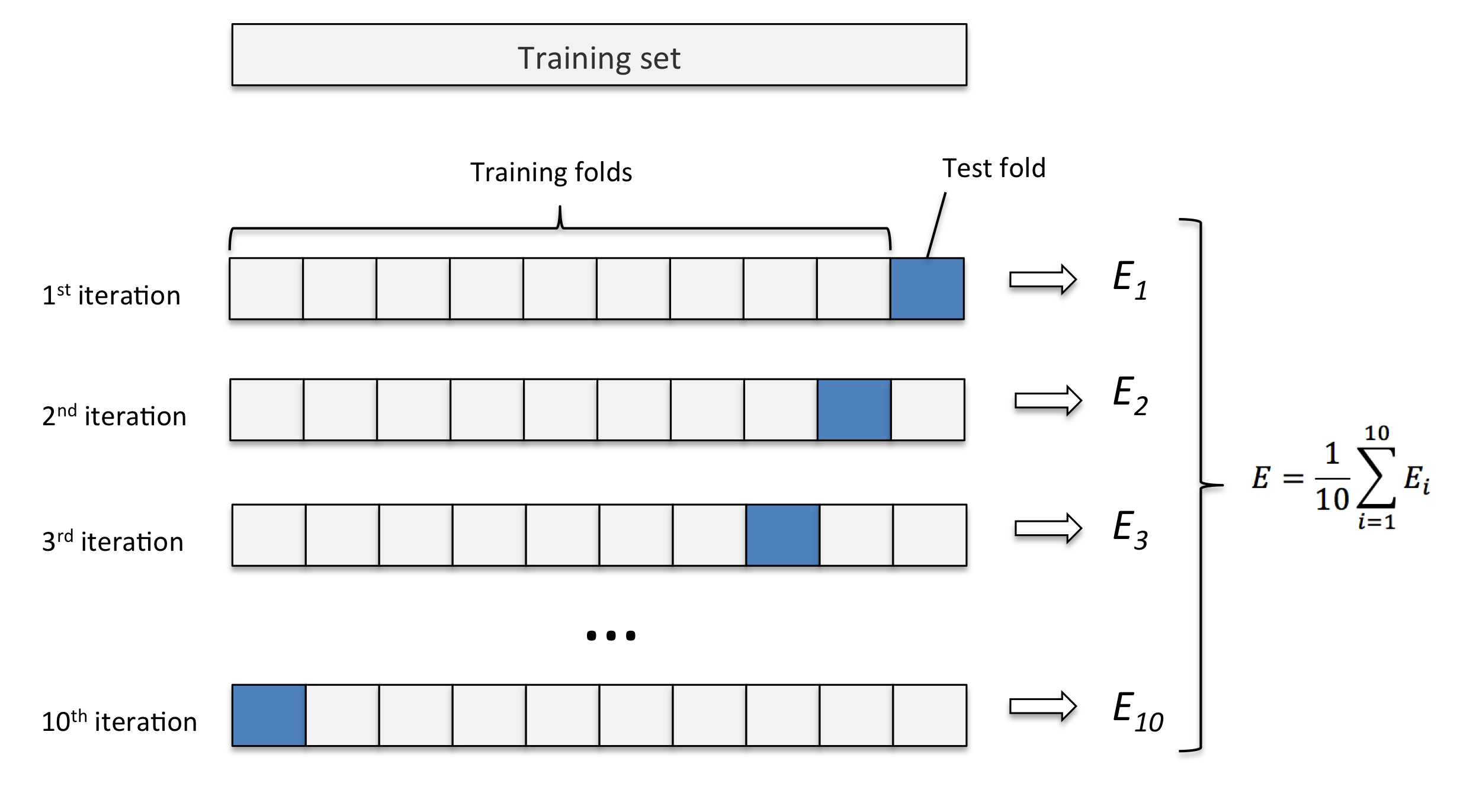
Quanto maior o k escolhido obtemos menos viés, porém mais variância. Em outras palavras, você terá uma estimativa muito precisa do viés entre os valores previstos e os valores verdadeiros, porém altamente variável. Agora quanto menor o k escolhido, mais viés e menos variância. Ou seja, não iremos necessariamente obter uma boa estimativa do viés, mas ela será menos variável.
OBS: Quando o k é igual ao tamanho da amostra, o método é também conhecido como leave-one-out.
Ex.: vamos utilizar reamostragem por k-fold no conjunto de dados spam.
library(caret)
library(kernlab)
data(spam)
noTreino = createDataPartition(y = spam$type, p = 0.75, list = F)
treino = spam[noTreino,]
teste = spam[-noTreino,]
# Para fazer a reamostragem por k-fold vamos utilizar o comando createFolds():
folds = createFolds(y = spam$type, k = 10, list = T, returnTrain = T)
Os principais argumentos da função createFolds() são:
- y = a variável de interesse (no nosso caso, o tipo do e-mail);
- k = o número (inteiro) de partições que você deseja.
- list = argumento do tipo logical. Se TRUE $\rightarrow$ os resultados serão mostrados em uma lista, se FALSE $\rightarrow$ os resultados serão mostrados em uma matriz.
- returnTrain = argumento do tipo logical. Se TRUE, retorna amostras treino. Se FALSE, retorna amostras teste.
Vamos verificar o tamanho de cada partição da nossa amostra treino:
sapply(folds,length)
## Fold01 Fold02 Fold03 Fold04 Fold05 Fold06 Fold07 Fold08 Fold09 Fold10
## 4141 4141 4141 4141 4140 4141 4141 4141 4141 4141
Agora vamos fazer o mesmo para a amostra teste:
folds = createFolds(y = spam$type, k = 10, list = T, returnTrain = F)
sapply(folds,length)
## Fold01 Fold02 Fold03 Fold04 Fold05 Fold06 Fold07 Fold08 Fold09 Fold10
## 459 460 460 460 460 461 460 461 460 460
Outra opção de realizar a reamostragem por k-fold é aplicá-la diretamente na função train.
controle = trainControl(method = "cv", number = 10)
modelo = caret::train(type ~ ., data = spam, method = "glm", trControl = controle)
Repeated K-fold
O repeated k-fold se resume a repetir o método k-fold várias vezes, com o objetivo de melhorar nossa reamostragem.
Ex.: Vamos aplicar um método de treino 3 vezes em 10 folds.
controle = trainControl(method = "repeatedcv", number = 10, repeats = 3)
modelo = caret::train(type ~ ., data = spam, method = "glm", trControl = controle)
Bootstrap
O bootstrap é uma técnica de reamostragem com o propósito de reduzir desvios e realizar amostragem dos dados de treino com repetições. Já vimos anteriormente que este é o método default do comando train(), onde é feito 25 reamostragens por bootstrap.
Embora esse seja o padrão podemos alterar através do comando trainControl(). Por exemplo, vamos alterar o número de reamostragens de 25 para 10.
controle = trainControl(method = "boot", number = 10)
modelo = train(type ~ ., data = spam, method = "glm", trControl = controle)
Podemos também realizarmos bootstrap fora da função train(), utilizando o comando createResample().
folds = createResample(y = spam$type, times = 10, list = F)
Comparando Funções Preditoras
Como já foi dito em capítulos anteriores, existem diversas formas de comparar preditores. Nesse capítulo, vamos estudar um meio de fazer isso e ver mais detalhadamente as medidas de comparação que o R retorna ao usarmos esse método.
Exemplo de Comparação de Regressores - base faithful
Vamos usar a base de dados faithful já presente no R.
data("faithful")
# verificando a estrutura da base
str(faithful)
## 'data.frame': 272 obs. of 2 variables:
## $ eruptions: num 3.6 1.8 3.33 2.28 4.53 ...
## $ waiting : num 79 54 74 62 85 55 88 85 51 85 ...
Note que a base apresenta apenas duas variáveis: eruptions, que contém uma amostra corresponde ao tempo em minutos que o gêiser Old Faithful permanece em erupção e waiting, que contém uma amostra correspondente ao tempo em minutos até a próxima erupção. Vamos tentar prever a variável waiting através da variável eruptions. Note ainda que a variável de interesse é quantitativa contínua, portanto queremos construir um regressor.
Vamos treinar nosso modelo utilizando 3 métodos separadamente: linear model, Projection Pursuit Regression e k-Nearest Neighbor. Para fazer a comparação, vamos colocar a mesma semente antes de cada treino para que todos sejam feitos da mesma forma e assim torne a comparação mais “justa”. Note também que estamos usando toda a base de dados pra treinar o medelo. Isso porque estamos apenas avaliando o melhor modelo.
library(caret)
# usando o método de validação cruzada tiramos a dependência da amostra
TC = trainControl(method="repeatedcv", number=10,repeats=3)
set.seed(371)
modelo_lm = train(waiting~eruptions, data=faithful, method="lm", trControl=TC)
set.seed(371)
modelo_ppr = train(waiting~eruptions, data=faithful, method="ppr", trControl=TC)
set.seed(371)
modelo_knn = train(waiting~eruptions, data=faithful, method="knn", trControl=TC)
Agora, como sabemos qual desses é o melhor modelo para nosso Regressor?
resultados = resamples(list(LM=modelo_lm, PPR=modelo_ppr, KNN=modelo_knn))
summary(resultados)
##
## Call:
## summary.resamples(object = resultados)
##
## Models: LM, PPR, KNN
## Number of resamples: 30
##
## MAE
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## LM 3.816660 4.396526 4.723050 4.792316 5.063279 6.087023 0
## PPR 3.847465 4.329571 4.638090 4.728487 5.133559 5.980745 0
## KNN 3.565922 4.380002 4.717796 4.735160 5.167973 5.909983 0
##
## RMSE
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## LM 4.769227 5.375918 5.919905 5.877351 6.204474 7.037539 0
## PPR 4.775950 5.258969 5.871960 5.725215 6.099465 6.865713 0
## KNN 4.564997 5.308376 5.828188 5.773268 6.275956 6.892789 0
##
## Rsquared
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## LM 0.7232859 0.7855436 0.8198045 0.8154236 0.8443912 0.8715797 0
## PPR 0.7461656 0.7964453 0.8243005 0.8241913 0.8567375 0.8812427 0
## KNN 0.7636897 0.7964592 0.8227743 0.8218778 0.8453996 0.8771367 0
Repare que foi calculada três diferentes medidas: “MAE”, “RMSE”, e “Rsquared”.
O Erro Médio Absoluto (MAE - Mean Absolute Error) é dado pelo média dos desvios absolutos. \(MAE = \frac{\sum\limits_{i=1}^{n}\mid estimado_i - real_i\mid}{n}\quad, i=1,2,...,n.\)
A Raiz do Erro Quadrático Médio (RMSE - Root Mean Squared Error), como o nome já diz, não é nada mais que a raiz quadrada do Erro Quadrático Médio já citado no capítulo de [Tipos de Erro]. \(RMSE=\sqrt{MSE}=\sqrt{\frac{\sum\limits_{i=1}^{n} \left( estimado_i-real_i \right)^{2}}{n}}\quad, i=1,2,...,n.\)
O Coeficiente de Determinação, Também chamado de $R^2$ (R squared), é dado pela razão entre o MSE e a Variância subtraído de 1. \(R^2 =1- \frac{MSE}{Var}= 1-\frac{\sum\limits_{i=1}^{n} (real_i - estimado_i)^2}{\sum\limits_{i=1}^{n} (real_i - média)^2}\quad, i=1,2,...,n.\)
Portanto, queremos o modelo que possua MAE e RMSE baixo e $R^2$ alto. Para vizualizar melhor, podemos construir um boxplot comparativo da seguinte forma:
# Ajustando as escalas dos gráficos:
escala <- list(x=list(relation="free"), y=list(relation="free"))
# Plotando os dados:
bwplot(resultados, scales=escala)
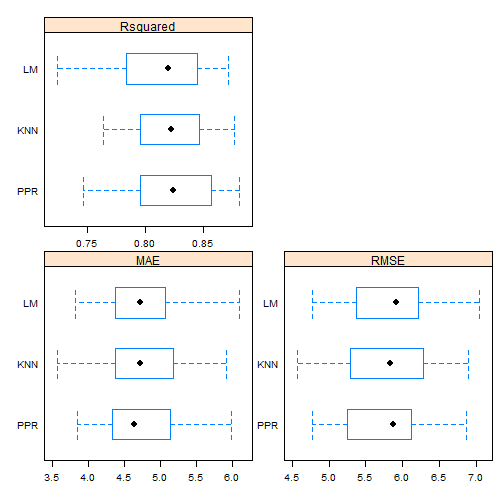
Pelos boxplots podemos perceber que o modelo linear é o que possui a pior mediana nas três medidas comparativas e parece ter os dados mais espalhados, principalmente no $R^2$, o que indica que ele possui alta variabilidade. Quanto ao KNN e o PPR, os dados estão mais concentrados no RMSE e no $R^2$, embora tenham bastante outliers. Parece que o PPR é levemente melhor que o KNN, mas é preciso uma análise mais profunda.
library(lattice)
# Comparando o comportamento de cada fold nos modelos KNN e PPR
xyplot(resultados, models=c("PPR", "KNN"))
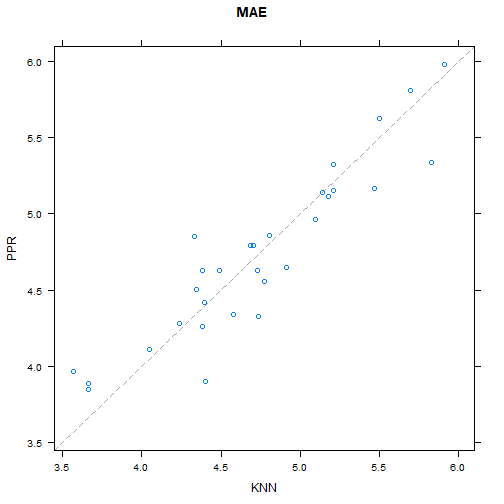
Note que a maior parte dos folds está acima da diagonal, indicando que o KNN tem um erro absoluto médio (MAE) menor que o PPR. Vamos olhar novamente para o cálculo que fizemos mais acima.
resultados = resamples(list(LM=modelo_lm, PPR=modelo_ppr, KNN=modelo_knn))
summary(resultados)
##
## Call:
## summary.resamples(object = resultados)
##
## Models: LM, PPR, KNN
## Number of resamples: 30
##
## MAE
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## LM 3.816660 4.396526 4.723050 4.792316 5.063279 6.087023 0
## PPR 3.847465 4.329571 4.638090 4.728487 5.133559 5.980745 0
## KNN 3.565922 4.380002 4.717796 4.735160 5.167973 5.909983 0
##
## RMSE
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## LM 4.769227 5.375918 5.919905 5.877351 6.204474 7.037539 0
## PPR 4.775950 5.258969 5.871960 5.725215 6.099465 6.865713 0
## KNN 4.564997 5.308376 5.828188 5.773268 6.275956 6.892789 0
##
## Rsquared
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## LM 0.7232859 0.7855436 0.8198045 0.8154236 0.8443912 0.8715797 0
## PPR 0.7461656 0.7964453 0.8243005 0.8241913 0.8567375 0.8812427 0
## KNN 0.7636897 0.7964592 0.8227743 0.8218778 0.8453996 0.8771367 0
Podemos notar que o KNN tem uma posição melhor que o PPR em todas as medidas. Como saber se essa diferença é significativa? Vamos calcular as diferenças entre os dois modelos e avaliar atravé do p-valor.
#Calcular diferença entre modelos, e realizar
#testes de hipótese para as diferenças.
diferencas = diff(resultados)
summary(diferencas)
##
## Call:
## summary.diff.resamples(object = diferencas)
##
## p-value adjustment: bonferroni
## Upper diagonal: estimates of the difference
## Lower diagonal: p-value for H0: difference = 0
##
## MAE
## LM PPR KNN
## LM 0.063829 0.057156
## PPR 0.18 -0.006673
## KNN 1.00 1.00
##
## RMSE
## LM PPR KNN
## LM 0.15214 0.10408
## PPR 0.002181 -0.04805
## KNN 0.422993 0.946570
##
## Rsquared
## LM PPR KNN
## LM -0.008768 -0.006454
## PPR 0.01111 0.002313
## KNN 0.54786 1.00000
Observe que, para cada medida, acima da diagonal temos a diferença entre os modelos e abaixo da diagonal o p-valor do teste de comparação entre eles. Portanto, se considerarmos um nível de significância de 1%, é razoável dizer que os modelos PPR e KKN produzem resultados significativamente diferentes. Sendo assim, escolheriamos o método KNN para treinar nosso modelo.
Exemplo de Comparação de Classificadores - base Heart
Suponha agora que queremos predizer se uma pessoa tem ou problema no coração dado que ela apresentou dor no peito. Considere a seguinte base de dados.
library(readr)
# lendo a base de dados
heart = read_csv("Heart.csv")
# verificando a estrutura da base
str(heart)
## tibble [297 x 15] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
## $ X1 : num [1:297] 1 2 3 4 5 6 7 8 9 10 ...
## $ Age : num [1:297] 63 67 67 37 41 56 62 57 63 53 ...
## $ Sex : num [1:297] 1 1 1 1 0 1 0 0 1 1 ...
## $ ChestPain : chr [1:297] "typical" "asymptomatic" "asymptomatic" "nonanginal" ...
## $ RestBP : num [1:297] 145 160 120 130 130 120 140 120 130 140 ...
## $ Chol : num [1:297] 233 286 229 250 204 236 268 354 254 203 ...
## $ Fbs : num [1:297] 1 0 0 0 0 0 0 0 0 1 ...
## $ RestECG : num [1:297] 2 2 2 0 2 0 2 0 2 2 ...
## $ MaxHR : num [1:297] 150 108 129 187 172 178 160 163 147 155 ...
## $ ExAng : num [1:297] 0 1 1 0 0 0 0 1 0 1 ...
## $ Oldpeak : num [1:297] 2.3 1.5 2.6 3.5 1.4 0.8 3.6 0.6 1.4 3.1 ...
## $ Slope : num [1:297] 3 2 2 3 1 1 3 1 2 3 ...
## $ Ca : num [1:297] 0 3 2 0 0 0 2 0 1 0 ...
## $ Thal : chr [1:297] "fixed" "normal" "reversable" "normal" ...
## $ HeartDisease: chr [1:297] "No" "Yes" "Yes" "No" ...
## - attr(*, "spec")=
## .. cols(
## .. X1 = col_double(),
## .. Age = col_double(),
## .. Sex = col_double(),
## .. ChestPain = col_character(),
## .. RestBP = col_double(),
## .. Chol = col_double(),
## .. Fbs = col_double(),
## .. RestECG = col_double(),
## .. MaxHR = col_double(),
## .. ExAng = col_double(),
## .. Oldpeak = col_double(),
## .. Slope = col_double(),
## .. Ca = col_double(),
## .. Thal = col_character(),
## .. HeartDisease = col_character()
## .. )
Note que a variável de interesse HeartDisease é categórica, portanto estamos trabalhando com um Classificador.
Vamos treinar nosso modelo utilizando 3 métodos separadamente: Recursive Partitioning and Regression Trees, Fitting Generalized Linear Models e Support Vector Machines. Novamente, vamos colocar a mesma semente antes de cada treino e utilizar toda a base de dados pra isso.
library(caret)
# usando o método de validação cruzada tiramos a dependência da amostra
TC = trainControl(method="repeatedcv", number=10,repeats=3)
set.seed(371)
modelo_rpart = caret::train(HeartDisease~., data=heart, method="rpart", trControl=TC)
set.seed(371)
modelo_glm = caret::train(HeartDisease~., data=heart, method="glm", trControl=TC)
set.seed(371)
modelo_svm = caret::train(HeartDisease~., data=heart, method="svmLinear", trControl=TC)
Assim como no caso anterior, vamos comparar os resultados obtidos por cada modelo.
resultados = resamples(list(Rpart=modelo_rpart, GLM=modelo_glm, SVM=modelo_svm))
summary(resultados)
##
## Call:
## summary.resamples(object = resultados)
##
## Models: Rpart, GLM, SVM
## Number of resamples: 30
##
## Accuracy
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## Rpart 0.5172414 0.7060345 0.7459770 0.7493103 0.8000000 0.8666667 0
## GLM 0.6896552 0.7948276 0.8477011 0.8438697 0.8916667 0.9666667 0
## SVM 0.6896552 0.8000000 0.8333333 0.8394253 0.8890805 1.0000000 0
##
## Kappa
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## Rpart 0.06451613 0.4105769 0.4971161 0.4956347 0.5973094 0.7368421 0
## GLM 0.34912718 0.5912008 0.6918699 0.6832658 0.7809134 0.9327354 0
## SVM 0.37708831 0.5912008 0.6651719 0.6740506 0.7727163 1.0000000 0
Repare que foi calculada duas diferentes medidas: “Accuracy”, e “Kappa”.
A Precisão (Accuracy) como já foi citado no capítulo [Introdução ao pacote caret], avalia a proporção de acertos na predição.\(Precisão=\frac{Predições\ corretas}{Total\ de\ predições}\)
O Coeficiente de concordância Kappa avalia o grau de concordância entre a classificação e o real valor de uma mesma amostra. E é calculado da seguinte forma:
Portanto, queremos que as duas medidas sejam altas. Vamos ver o boxplot.
# ajustando as escalas dos graficos
escala <- list(x=list(relation="free"), y=list(relation="free"))
# plotando os dados
bwplot(resultados, scales=escala)
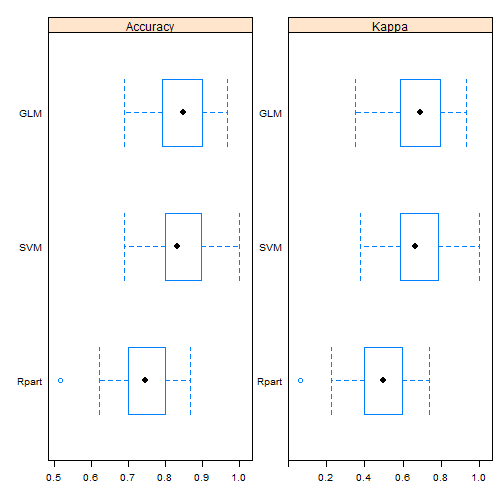
Pelo boxplot podemos ver que o método Rpart possui uma alta variabilidade. O método GLM está com uma mediana melhor e parece mais concentrado. Mas será que ele é mesmo melhor que o SVM?
# Comparando o comportamento de cada fold nos modelos KNN e PPR
xyplot(resultados, models=c("GLM", "SVM"))
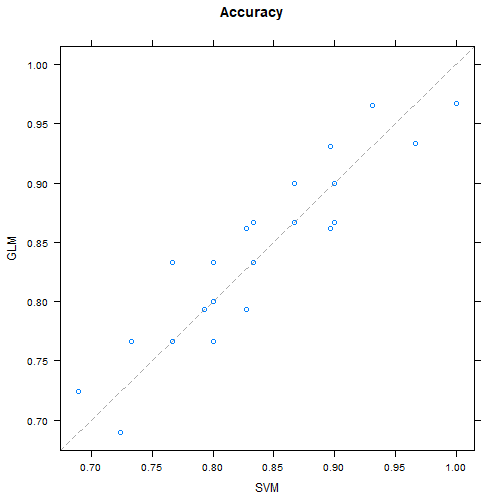
Por esse plot, não parece haver uma diferença significativa entre os dois métodos. Vamos voltar a nossas medidas.
resultados = resamples(list(Rpart=modelo_rpart, GLM=modelo_glm, SVM=modelo_svm))
summary(resultados)
##
## Call:
## summary.resamples(object = resultados)
##
## Models: Rpart, GLM, SVM
## Number of resamples: 30
##
## Accuracy
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## Rpart 0.5172414 0.7060345 0.7459770 0.7493103 0.8000000 0.8666667 0
## GLM 0.6896552 0.7948276 0.8477011 0.8438697 0.8916667 0.9666667 0
## SVM 0.6896552 0.8000000 0.8333333 0.8394253 0.8890805 1.0000000 0
##
## Kappa
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## Rpart 0.06451613 0.4105769 0.4971161 0.4956347 0.5973094 0.7368421 0
## GLM 0.34912718 0.5912008 0.6918699 0.6832658 0.7809134 0.9327354 0
## SVM 0.37708831 0.5912008 0.6651719 0.6740506 0.7727163 1.0000000 0
A precisão e kappa média também parecem próximas entre o GLM e o SVM. Vamos fazer então um teste de hipótese para confirmar.
#Calcular diferença entre modelos, e realizar
#testes de hipótese para as diferenças.
diferencas = diff(resultados)
summary(diferencas)
##
## Call:
## summary.diff.resamples(object = diferencas)
##
## p-value adjustment: bonferroni
## Upper diagonal: estimates of the difference
## Lower diagonal: p-value for H0: difference = 0
##
## Accuracy
## Rpart GLM SVM
## Rpart -0.094559 -0.090115
## GLM 0.000000002107 0.004444
## SVM 0.000000011839 1
##
## Kappa
## Rpart GLM SVM
## Rpart -0.187631 -0.178416
## GLM 0.00000000237 0.009215
## SVM 0.00000001173 1
Note que o p-valor da diferença é 1. Portanto, concluímos que não existe uma diferença significativa entre os métodos GLM e SVM para este caso.
Mas, e quanto ao tempo de processamento de cada modelo? Vamos usar a função Sys.time() para medir o tempo de treinamento nos dois métodos.
inicio1 <- Sys.time()
set.seed(371)
modelo_glm = train(HeartDisease~., data=heart, method="glm", trControl=TC)
fim1 <- Sys.time()
fim1 - inicio1
## Time difference of 1.028369 secs
inicio2 <- Sys.time()
set.seed(371)
modelo_svm = train(HeartDisease~., data=heart, method="svmLinear", trControl=TC)
fim2 <- Sys.time()
fim2 - inicio2
## Time difference of 1.108321 secs
Bem, não parece que a diferença foi muito grande. Mas, pense agora que você quer realizar uma comparação usando a validação cruzada com 20 folds e 100 repetições.
TC = trainControl(method="repeatedcv", number=20,repeats=100)
inicio1 <- Sys.time()
set.seed(371)
modelo_glm = train(HeartDisease~., data=heart, method="glm", trControl=TC)
fim1 <- Sys.time()
fim1 - inicio1
## Time difference of 27.45612 secs
inicio2 <- Sys.time()
set.seed(371)
modelo_svm = train(HeartDisease~., data=heart, method="svmLinear", trControl=TC)
fim2 <- Sys.time()
fim2 - inicio2
## Time difference of 34.9665 secs
A diferença de processamento agora já é um pouco maior. Mas, lembre que nossa base de dados contém apenas 297 observações e 15 variáveis. Numa base de dados muito grande e/ou em determinados métodos esse tempo fará diferença.
Pré-Processamento
Antes de criarmos um modelo de predição, é importante plotarmos as variáveis do nosso modelo antecipadamente para observarmos se há algum comportamento estranho entre elas. Por exemplo, podemos ter uma variável que assuma frequentemente um único valor (possui muito pouca variabilidade), o que não acrescenta informações relevantes ao modelo, ou uma que possua alguns dados faltantes (NA’s). O que podemos fazer nesses casos, que é o que iremos estudar neste capítulo, é realizar alterações em tais variáveis, afim de melhorar/otimizar a nossa predição/classificação. Essa é a ideia de pré-processar.
Padronizando os Dados
Vamos carregar o banco de dados spam e criar amostras treino e teste.
library(kernlab)
library(caret)
data(spam)
set.seed(123)
noTreino = createDataPartition(y = spam$type, p = 0.75, list = F)
treino = spam[noTreino,]
teste = spam[-noTreino,]
# Vamos olhar para a variável capitalAve (média de letras maiúsculas por linha):
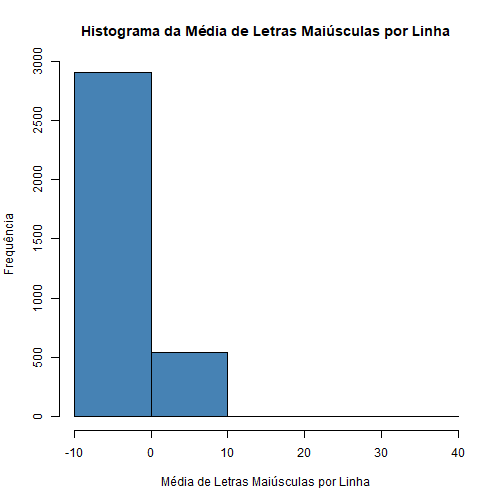
hist(treino$capitalAve,
ylab = "Frequência",
xlab = "Média de Letras Maiúsculas por Linha",
main = "Histograma da Média de Letras Maiúsculas por Linha",
col="steelblue", breaks = 4)
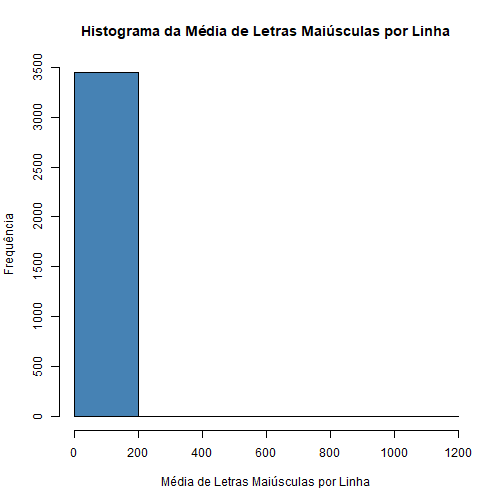
Podemos notar que muitos elementos estão próximos do 0 e os outros estão muito espalhados. Ou seja, essa variável não está trazendo muita informação para o modelo.
mean(treino$capitalAve)
## [1] 4.863991
sd(treino$capitalAve)
## [1] 27.80173
Podemos ver que a média é pequena mas o desvio padrão é muito grande.
Para que os algoritmos de machine learning não sejam enganados pelo fato de a variável ser altamente variável, vamos realizar um pré-processamento. Vamos padronizar os dados da variável pela amostra treino pegando cada valor dela e subtraindo pela sua média e dividindo pelo seu desvio padrão.
treinoCapAve = treino$capitalAve
# Padronizando a variável:
treinoCapAveP = (treino$capitalAve-mean(treinoCapAve))/sd(treinoCapAve)
# Média da variável padronizada:
mean(treinoCapAveP)
## [1] 0.000000000000000009854945
Agora temos média 0.
# Desvio padrão da variável padronizada:
sd(treinoCapAveP)
## [1] 1
E variância 1.
# Vamos olhar para a variável capitalAve (média de letras maiúsculas por linha):
hist(treinoCapAveP, ylab = "Frequência", xlab = "Média de Letras Maiúsculas por Linha",
main = "Histograma da Média de Letras Maiúsculas por Linha",col="steelblue", breaks =4)
Agora vamos aplicar a mesma transformação na amostra teste. Uma coisa a ter em mente é que ao aplicar um algoritmo no conjunto de teste, só podemos usar os parâmetros que estimamos no conjunto de treino. Ou seja, temos que usar a média e o desvio padrão da variável capitalAve do TREINO.
testeCapAve = teste$capitalAve
# Aplicando a transformação:
testeCapAveP = (testeCapAve-mean(treinoCapAve))/sd(treinoCapAve)
# Média da variável transformada do conjunto teste:
mean(testeCapAveP)
## [1] 0.04713308
# Desvio Padrão da variável transformada do conjunto teste:
sd(testeCapAveP)
## [1] 1.486708
Nesse caso não obtemos média 0 e variância 1, afinal nós utilizamos os parâmetros do treino para a padronização. Mas podemos notar que os valores estão relativamente próximos disso.
Padronizando os Dados com a Função preProcess()
Podemos realizar o pré-processamento utilizando a função preProcess() do caret. Ela realiza vários tipos de padronizações, mas para utilizarmos a mesma (subtrair a média e dividir pelo desvio padrão) utilizamos o método c(“center”,”scale”).
padronizacao = preProcess(treino, method = c("center","scale"))
# O comando acima cria um modelo de padronização. Para ter efeito ele deve ser aplicado nos dados com o
# comando predict().
treinoCapAveS = predict(padronizacao,treino)$capitalAve
# Média da variável padronizada:
mean(treinoCapAveS)
## [1] 0.000000000000000008680584
# Desvio padrão da variável padronizada:
sd(treinoCapAveS)
## [1] 1
Note que chegamos à mesma média e variância de quando padronizamos sem o preProcess().
Agora vamos aplicar essa padronização no conjunto de teste:
testeCapAveS = predict(padronizacao,teste)$capitalAve
# Note que aplicamos o modelo de padronização criado com a amostra treino.
Observe que também encontramos o mesmo valor da média e desvio padrão de quando padronizamos a variável do conjunto teste anteriormente (sem o preProcess()):
mean(testeCapAveS)
## [1] 0.04713308
sd(testeCapAveS)
## [1] 1.486708
Repare que também chegamos à mesma média e variância de quando padronizamos sem o preProcess().
preProcess como argumento da função train()
Também podemos utilizar o preProcess dentro da função train da seguinte forma:
modelo = train(type~., data = treino, preProcess = c("center","scale"),
method = "glm")
A única limitação é que esse método aplica a padronização em todas as variáveis numéricas.
Obs.: Quando for padronizar uma variável da sua base para depois treinar seu algoritmo, lembre-se que colocar a variável padronizada de volta na sua base.
Tratando NA’s
É muito comum encontrar alguns dados faltantes (NA’s) em uma base de dados. E quando você usa essa base para fazer predições, o algoritmo preditor muitas vezes falha, pois eles são criados para não manipular dados ausentes (na maioria dos casos). O mais recomendado a se fazer é descartar esses dados, principalmente se o número de variáveis for muito pequeno. Porém, em alguns casos, podemos tentar substituir os NA’s da amostra por dados de outros elementos que possuam características parecidas.
Obs: Este é um procedimento que deve ser feito com muito cuidado, apenas em situações de real necessidade.
Método k-Nearest Neighbors (knn)
O método k-Nearest Neighbors (knn) consiste em procurar os k vizinhos mais próximos do elemento que possui o dado faltante de uma variável de interesse, calculando a média dos valores observados dessa variável dos k vizinhos e imputando esse valor ao elemento.
Vamos utilizar novamente a variável capitalAve do banco de dados spam como exemplo.
library(kernlab)
library(caret)
data(spam)
set.seed(13343)
# Criando amostras treino e teste:
noTreino = createDataPartition(y = spam$type, p = 0.75, list = F)
treino = spam[noTreino,]
teste = spam[-noTreino,]
Originalmente, a variável capitalAve não possui NA’s. Mas para o objetivo de compreendermos como esse método funciona, vamos inserir alguns valores NA’s.
NAs = rbinom(dim(treino)[1], size = 1, p = 0.05)==1
O que fizemos com a função rbinom() é criar uma amostra de tamanho “dim(treino)[1]” (quantidade de elementos no treino) de uma variável Bernoulli com probabilidade de sucesso = 0,05. Ou seja, o vetor NAs será um vetor do tipo logical, onde será TRUE se o elemento gerado pela rbinom() é “1” (probabilidade de 0,05 de acontecer) e FALSE se é “0” (probabilidade 0,95 de acontecer).
Para preservar os valores originais, vamos criar uma nova coluna de dados no treino chamada capAve, que será uma réplica da variável capitalAve, mas com os NA’s inseridos em alguns valores.
library(dplyr)
# Criando a nova variável capAve com os mesmos valores da capitalAve:
treino = treino %>% mutate(capAve = capitalAve)
# Inserindo os Na's:
treino$capAve[NAs] = NA
Agora podemos aplicar o método KNN para imputar valores aos NA’s, escolhendo essa opção por meio do argumento “method” da função preProcess(). O padrão da função é utilizar k=5.
imput = preProcess(treino, method = "knnImpute")
# Aplicando o modelo de pré-processamento ao banco de dados treino:
treino$capAve = predict(imput,treino)$capAve
# Olhando para a variável capAve após o pré-processamento:
head(treino$capAve, n = 20)
## [1] -0.046596612 -0.008173931 0.125003949 -0.052792906 -0.052792906 -0.067986558 -0.105588726 -0.083548027 0.122825344
## [10] -0.115746121 -0.047388832 -0.093931771 -0.097100652 -0.021245565 0.850451334 -0.115519772 -0.044418006 -0.015445381
## [19] -0.120867259 0.001785409
Note que além de ter imputado valores aos NA’s, o comando knnImpute também padronizou os dados.
OBS: O método knnImpute só resolve os NA’s quando os dados faltantes são NUMÉRICOS.
E se quiséssemos aplicar o método de imputar valores aos NA’s em todo o conjunto de dados, e não só em apenas 1 variável? Também podemos fazer isso utilizando a função preProcess().
Vamos utilizar a base de dados “airquality”, já disponível no R, como exemplo.
base = airquality
head(base, n = 15)
## Ozone Solar.R Wind Temp Month Day
## 1 41 190 7.4 67 5 1
## 2 36 118 8.0 72 5 2
## 3 12 149 12.6 74 5 3
## 4 18 313 11.5 62 5 4
## 5 NA NA 14.3 56 5 5
## 6 28 NA 14.9 66 5 6
## 7 23 299 8.6 65 5 7
## 8 19 99 13.8 59 5 8
## 9 8 19 20.1 61 5 9
## 10 NA 194 8.6 69 5 10
## 11 7 NA 6.9 74 5 11
## 12 16 256 9.7 69 5 12
## 13 11 290 9.2 66 5 13
## 14 14 274 10.9 68 5 14
## 15 18 65 13.2 58 5 15
Note que essa base possui alguns valores NA’s em algumas variáveis.
# Realizando o método KNN para imputar valores aos NA's:
imput = preProcess(base, method = "knnImpute")
# Aplicando o modelo em toda a base de dados:
nova_base = predict(imput, base)
# Vamos olhar para a nova base:
head(nova_base, n = 15)
## Ozone Solar.R Wind Temp Month Day
## 1 -0.03423409 0.045176154 -0.72594816 -1.1497140 -1.407294 -1.6700195
## 2 -0.18580489 -0.754304874 -0.55563883 -0.6214670 -1.407294 -1.5572102
## 3 -0.91334473 -0.410083876 0.75006604 -0.4101682 -1.407294 -1.4444009
## 4 -0.73145977 1.410956244 0.43783226 -1.6779609 -1.407294 -1.3315917
## 5 -0.81027658 -0.221317522 1.23260914 -2.3118573 -1.407294 -1.2187824
## 6 -0.42831817 0.007422883 1.40291847 -1.2553634 -1.407294 -1.1059732
## 7 -0.57988897 1.255501599 -0.38532950 -1.3610128 -1.407294 -0.9931639
## 8 -0.70114561 -0.965279034 1.09068470 -1.9949091 -1.407294 -0.8803546
## 9 -1.03460136 -1.853591288 2.87893266 -1.7836103 -1.407294 -0.7675454
## 10 -0.64051729 0.089591767 -0.38532950 -0.9384152 -1.407294 -0.6547361
## 11 -1.06491552 0.749163615 -0.86787260 -0.4101682 -1.407294 -0.5419268
## 12 -0.79208809 0.778033763 -0.07309573 -0.9384152 -1.407294 -0.4291176
## 13 -0.94365889 1.155566471 -0.21502017 -1.2553634 -1.407294 -0.3163083
## 14 -0.85271641 0.977904020 0.26752293 -1.0440646 -1.407294 -0.2034991
## 15 -0.73145977 -1.342811742 0.92037537 -2.1005585 -1.407294 -0.0906898
Note que ela não possui mais NA’s e todas as variáveis foram padronizadas.
Utilizando Algoritmos de Machine Learning com o Pacote mlr
O pacote mlr fornece vários métodos de imputação para dados faltantes. Alguns desses métodos possuem técnicas padrões como, por exemplo, imputação por uma constante (uma constante fixa, a média, a mediana ou a moda) ou números aleatórios (da distribuição empírica dos dados em consideração ou de uma determinada família de distribuições). Para mais informações sobre como utilizar essas imputações padrões, consulte https://mlr.mlr-org.com/reference/imputations.html.
Entretanto, a principal vantagem desse pacote - que é o que abordaremos nessa seção - é a possibilidade de imputação dos valores faltantes de uma variável por meio de predições de um algoritmo de machine learning, utilizando como base as outras variáveis. Ou seja, além de aceitar valores faltantes de variáveis numéricas para a imputação, ele também aceita de variáveis categóricas.
Podemos observar todos os algoritmos de machine learning possíveis de serem utilizados nesse pacote através da função listLearners().
- Para um problema de imputação de NA’s de variáveis numéricas temos os seguintes métodos:
library(mlr)
knitr::kable(listLearners("regr", properties = "missings")["class"])
| class |
|---|
| regr.bartMachine |
| regr.cforest |
| regr.ctree |
| regr.cubist |
| regr.featureless |
| regr.gbm |
| regr.h2o.deeplearning |
| regr.h2o.gbm |
| regr.h2o.glm |
| regr.h2o.randomForest |
| regr.randomForestSRC |
| regr.rpart |
| regr.xgboost |
- Para um problema de imputação de NA’s de variáveis categóricas temos os seguintes métodos:
knitr::kable(listLearners("classif", properties = "missings")["class"])
| class |
|---|
| classif.bartMachine |
| classif.boosting |
| classif.C50 |
| classif.cforest |
| classif.ctree |
| classif.featureless |
| classif.gbm |
| classif.h2o.deeplearning |
| classif.h2o.gbm |
| classif.h2o.glm |
| classif.h2o.randomForest |
| classif.J48 |
| classif.JRip |
| classif.naiveBayes |
| classif.OneR |
| classif.PART |
| classif.randomForestSRC |
| classif.rpart |
| classif.xgboost |
Vamos utilizar o banco de dados “heart” para realizarmos a imputação de dados faltantes categóricos.
library(caret)
library(readr)
library(dplyr)
heart = read_csv("Heart.csv")
# Verificando se a base "heart" possui valores NA's em alguma variável:
apply(heart, 2, function(x) any(is.na(x)))
## X1 Age Sex ChestPain RestBP Chol Fbs RestECG MaxHR
## FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## ExAng Oldpeak Slope Ca Thal HeartDisease
## FALSE FALSE FALSE FALSE FALSE FALSE
Note que a base não possui dados faltantes. Para fins didáticos, vamos inserir alguns na variável “Thal”.
# Criando um novo banco de dados que possuirá NA's:
new.heart = as.data.frame(heart)
set.seed(133)
# Criando um vetor do tipo *logical*, onde será TRUE se o elemento gerado pela rbinom() é "1"
# (probabilidade de 0,1 de acontecer):
NAs = rbinom(dim(new.heart)[1], size = 1, p = 0.1)==1
# Inserindo os NA's na variável Thal:
new.heart$Thal[NAs] = NA
new.heart$Thal
## [1] "fixed" "normal" "reversable" "normal" "normal" "normal" "normal" "normal"
## [9] "reversable" "reversable" "fixed" "normal" "fixed" "reversable" "reversable" "normal"
## [17] "reversable" "normal" "normal" "normal" NA "normal" "normal" "reversable"
## [25] "reversable" "normal" "normal" "normal" "normal" NA "normal" "reversable"
## [33] "normal" "reversable" "normal" "normal" "reversable" "fixed" "reversable" "normal"
## [41] "reversable" "reversable" "normal" "normal" "normal" "reversable" "normal" "reversable"
## [49] "normal" "normal" "normal" "reversable" "normal" "normal" "reversable" NA
## [57] "reversable" "reversable" "normal" "normal" NA "normal" "reversable" "normal"
## [65] NA "reversable" "normal" "reversable" "reversable" "normal" "normal" "reversable"
## [73] "reversable" "fixed" NA "normal" "reversable" "normal" "normal" NA
## [81] "normal" "normal" "normal" "reversable" "normal" "normal" "normal" "normal"
## [89] "normal" "normal" "reversable" "reversable" "normal" "normal" "reversable" "reversable"
## [97] "reversable" "normal" "normal" "normal" "normal" NA "normal" "reversable"
## [105] "reversable" "reversable" "reversable" "reversable" "reversable" "reversable" "normal" "fixed"
## [113] "reversable" "reversable" "fixed" "normal" "normal" "reversable" "reversable" "reversable"
## [121] "reversable" "normal" NA "normal" NA "reversable" "reversable" "normal"
## [129] "normal" "reversable" "reversable" "normal" "normal" "normal" "normal" NA
## [137] "reversable" "reversable" "normal" "normal" "reversable" "normal" "reversable" "reversable"
## [145] "normal" "reversable" "normal" "normal" NA "reversable" "normal" "reversable"
## [153] "reversable" "normal" "normal" "reversable" "reversable" NA "reversable" "reversable"
## [161] NA "normal" "normal" "normal" "reversable" "normal" NA "normal"
## [169] "reversable" "reversable" "normal" "normal" "fixed" "reversable" "reversable" "fixed"
## [177] "normal" "normal" "reversable" "reversable" "normal" "reversable" "normal" "normal"
## [185] "reversable" "fixed" "reversable" "reversable" "normal" "reversable" "normal" "normal"
## [193] "normal" "normal" "normal" "normal" "normal" "normal" "normal" NA
## [201] "reversable" NA "reversable" NA "reversable" "normal" "normal" "normal"
## [209] "reversable" "normal" "reversable" "normal" "reversable" "normal" "normal" "normal"
## [217] "normal" "normal" "normal" "normal" "reversable" "normal" "normal" "normal"
## [225] "normal" "normal" "normal" "normal" "normal" NA "normal" "normal"
## [233] "normal" "reversable" "reversable" "normal" "normal" "normal" "normal" "normal"
## [241] "normal" "normal" "normal" "reversable" "normal" "reversable" "normal" "fixed"
## [249] "reversable" "reversable" "normal" "normal" "normal" "normal" "normal" "normal"
## [257] "reversable" "normal" "normal" "normal" "normal" "normal" "fixed" "fixed"
## [265] "reversable" "normal" "reversable" "fixed" "reversable" "normal" "normal" "reversable"
## [273] "normal" "normal" "normal" "normal" "reversable" "normal" "reversable" NA
## [281] "reversable" "fixed" "fixed" "reversable" "normal" "reversable" "normal" "fixed"
## [289] "reversable" "normal" NA "fixed" NA "reversable" "reversable" "reversable"
## [297] "normal"
Agora vamos imputar categorias aos dados faltantes da variável Thal. Iremos fazer isso através da função impute(). O único problema é que possuímos variáveis do tipo character na base de dados, e a função não aceita esta classe nos dados.
str(new.heart)
## 'data.frame': 297 obs. of 15 variables:
## $ X1 : num 1 2 3 4 5 6 7 8 9 10 ...
## $ Age : num 63 67 67 37 41 56 62 57 63 53 ...
## $ Sex : num 1 1 1 1 0 1 0 0 1 1 ...
## $ ChestPain : chr "typical" "asymptomatic" "asymptomatic" "nonanginal" ...
## $ RestBP : num 145 160 120 130 130 120 140 120 130 140 ...
## $ Chol : num 233 286 229 250 204 236 268 354 254 203 ...
## $ Fbs : num 1 0 0 0 0 0 0 0 0 1 ...
## $ RestECG : num 2 2 2 0 2 0 2 0 2 2 ...
## $ MaxHR : num 150 108 129 187 172 178 160 163 147 155 ...
## $ ExAng : num 0 1 1 0 0 0 0 1 0 1 ...
## $ Oldpeak : num 2.3 1.5 2.6 3.5 1.4 0.8 3.6 0.6 1.4 3.1 ...
## $ Slope : num 3 2 2 3 1 1 3 1 2 3 ...
## $ Ca : num 0 3 2 0 0 0 2 0 1 0 ...
## $ Thal : chr "fixed" "normal" "reversable" "normal" ...
## $ HeartDisease: chr "No" "Yes" "Yes" "No" ...
## - attr(*, "spec")=
## .. cols(
## .. X1 = col_double(),
## .. Age = col_double(),
## .. Sex = col_double(),
## .. ChestPain = col_character(),
## .. RestBP = col_double(),
## .. Chol = col_double(),
## .. Fbs = col_double(),
## .. RestECG = col_double(),
## .. MaxHR = col_double(),
## .. ExAng = col_double(),
## .. Oldpeak = col_double(),
## .. Slope = col_double(),
## .. Ca = col_double(),
## .. Thal = col_character(),
## .. HeartDisease = col_character()
## .. )
Vamos transformar essas categorias em fatores.
new.heart = mutate_if(new.heart, is.character, as.factor)
Vamos separar os dados em treino e teste.
set.seed(133)
noTreino = caret::createDataPartition(y = new.heart$HeartDisease, p = 0.75,
list = F)
treino = new.heart[noTreino,]
teste = new.heart[-noTreino,]
Agora vamos imputar os dados no conjunto treino com a função impute().
Para isso passamos como argumento:
-
A base de dados que possui os valores faltantes;
-
A variável resposta do modelo, ou seja, a variável de interesse para predição. No nosso exemplo essa variável é a “HeartDisease”, que indica se uma pessoa possui uma doença cardíaca;
-
Lista contendo o método de imputação para cada coluna do banco de dados. Como apenas temos NA’s na variável “Thal”, a lista só possuirá essa variável, seguida do método de imputação que desejamos para ela. Vamos utilizar o método de árvores de decisão (“rpart”).
treino = mlr::impute(treino, target = "HeartDisease",
cols = list(Thal = imputeLearner("classif.rpart")))
Essa função retorna uma lista de tamanho 2, onde primeiro se encontra a base de dados após a imputação dos valores e em seguida detalhes do método utilizado.
Vamos olhar para a variável após a imputação dos dados:
treino$data[,"Thal"]
## [1] normal normal normal normal normal normal reversable reversable fixed normal
## [11] fixed reversable normal normal normal reversable reversable reversable normal normal
## [21] normal normal reversable normal normal reversable reversable reversable normal reversable
## [31] reversable normal reversable normal normal normal normal reversable normal normal
## [41] reversable reversable reversable reversable normal normal reversable normal reversable reversable
## [51] reversable normal normal reversable reversable fixed reversable normal reversable normal
## [61] normal reversable normal normal normal reversable normal normal normal normal
## [71] normal reversable reversable normal reversable reversable reversable normal normal normal
## [81] reversable reversable reversable reversable reversable reversable fixed normal reversable reversable
## [91] normal reversable normal normal reversable reversable normal normal normal normal
## [101] normal reversable reversable normal reversable normal normal reversable normal normal
## [111] normal reversable reversable normal normal reversable reversable normal normal normal
## [121] reversable reversable normal reversable reversable normal normal reversable reversable fixed
## [131] normal normal reversable reversable reversable normal normal fixed reversable reversable
## [141] normal reversable normal normal normal normal normal normal reversable reversable
## [151] reversable reversable reversable reversable normal normal reversable reversable normal normal
## [161] normal normal normal reversable normal normal normal normal normal normal
## [171] normal normal normal normal normal reversable reversable normal normal normal
## [181] normal normal reversable reversable normal fixed reversable normal normal normal
## [191] normal normal reversable normal normal normal fixed fixed reversable normal
## [201] reversable fixed reversable normal reversable normal normal normal normal reversable
## [211] normal reversable reversable fixed fixed reversable normal normal fixed reversable
## [221] normal normal normal
## Levels: fixed normal reversable
Para implementarmos esse algoritmo no conjunto de dados teste basta utilizarmos a função reimpute() que implementaremos o mesmo método com os mesmos critérios criados no conjuno treino. Basta passar os seguintes argumentos:
-
A base de dados que possui os valores faltantes;
-
O mesmo método utilizado no treino.
A função retorna a base de dados com os valores imputados.
teste = reimpute(teste, treino$desc)
teste$Thal
## [1] fixed reversable reversable reversable normal normal normal reversable normal normal
## [11] fixed normal normal reversable normal normal normal reversable normal normal
## [21] normal normal normal reversable normal reversable reversable fixed normal reversable
## [31] reversable normal reversable reversable normal normal reversable reversable normal reversable
## [41] reversable reversable reversable normal normal fixed normal reversable normal normal
## [51] normal normal normal reversable normal normal normal normal normal normal
## [61] normal normal reversable normal normal normal normal normal reversable normal
## [71] fixed reversable reversable reversable
## Levels: fixed normal reversable
Variável Dummy
As variáveis dummies ou variáveis indicadoras são formas de agregar informações qualitativas em modelos estatísticos. Ela atribui 1 se o elemento possui determinada característica, ou 0 caso ele não possua. Esse tipo de transformação é importante para modelos de regressão pois ela torna possível trabalhar com variáveis qualitativas.
Vamos utilizar o banco de dados Wage, do pacote ISLR. Este banco possui informações sobre 3000 trabalhadores do sexo masculino de uma região dos EUA, como por exemplo idade (age), tipo de trabalho (jobclass), salário (wage), entre outras. Nosso objetivo é tentar prever o salário do indivíduo em função das outras variáveis.
library(ISLR)
data(Wage)
head(Wage)
## year age maritl race education region jobclass health health_ins
## 231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic 1. Industrial 1. <=Good 2. No
## 86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic 2. Information 2. >=Very Good 2. No
## 161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic 1. Industrial 1. <=Good 1. Yes
## 155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic 2. Information 2. >=Very Good 1. Yes
## 11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic 2. Information 1. <=Good 1. Yes
## 376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic 2. Information 2. >=Very Good 1. Yes
## logwage wage
## 231655 4.318063 75.04315
## 86582 4.255273 70.47602
## 161300 4.875061 130.98218
## 155159 5.041393 154.68529
## 11443 4.318063 75.04315
## 376662 4.845098 127.11574
Vamos olhar para 2 variáveis: jobclass (tipo de trabalho) e health_ins (indica se o trabalhador possui plano de saúde).
library(ggplot2)
Wage %>% ggplot(aes(x=jobclass)) + geom_bar(aes(fill=jobclass)) +
ylab("Frequência") + guides(fill=F) + theme_light() +
ggtitle("Gráfico de Barras para o Tipo de Trabalho")
Wage %>% ggplot(aes(x=health_ins)) + geom_bar(aes(fill=health_ins)) +
ylab("Frequência") + guides(fill=F) + theme_light() +
ggtitle("Gráfico de Barras para o Plano de Saúde")
Vamos transformar essas 2 variáveis em dummies por meio da função dummyVars().
dummies = dummyVars(wage~jobclass+health_ins, data = Wage)
# Aplicando ao modelo:
Dummies = predict(dummies, newdata = Wage)
head(Dummies)
## jobclass.1. Industrial jobclass.2. Information health_ins.1. Yes health_ins.2. No
## 231655 1 0 0 1
## 86582 0 1 0 1
## 161300 1 0 1 0
## 155159 0 1 1 0
## 11443 0 1 1 0
## 376662 0 1 1 0
Note que ele transforma cada categoria numa variável dummy. Ou seja, como temos 2 categorias para jobclass, cada uma delas vira uma variável dummy. Então se para um indivíduo temos um “1” na categoria “jobclass=industrial”, isso implica que terá um “0” na categoria “jobclass=information”, pois ou o indivíduo tem um tipo de trabalho, ou tem outro. O mesmo vale para as categorias de plano de saúde.
Observe também que esse novo modelo criado é uma matriz:
class(Dummies)
## [1] "matrix" "array"
Vamos anexar esse novo objeto aos dados:
Wage_dummy = cbind(Wage, Dummies)
head(Wage_dummy)
## year age maritl race education region jobclass health health_ins
## 231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic 1. Industrial 1. <=Good 2. No
## 86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic 2. Information 2. >=Very Good 2. No
## 161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic 1. Industrial 1. <=Good 1. Yes
## 155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic 2. Information 2. >=Very Good 1. Yes
## 11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic 2. Information 1. <=Good 1. Yes
## 376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic 2. Information 2. >=Very Good 1. Yes
## logwage wage jobclass.1. Industrial jobclass.2. Information health_ins.1. Yes health_ins.2. No
## 231655 4.318063 75.04315 1 0 0 1
## 86582 4.255273 70.47602 0 1 0 1
## 161300 4.875061 130.98218 1 0 1 0
## 155159 5.041393 154.68529 0 1 1 0
## 11443 4.318063 75.04315 0 1 1 0
## 376662 4.845098 127.11574 0 1 1 0
# Removendo as variáveis categóricas do banco de dados completo (opcional):
Wage_dummy = dplyr::select(Wage_dummy, -c(jobclass,health_ins))
head(Wage_dummy)
## year age maritl race education region health logwage wage
## 231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic 1. <=Good 4.318063 75.04315
## 86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic 2. >=Very Good 4.255273 70.47602
## 161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic 1. <=Good 4.875061 130.98218
## 155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic 2. >=Very Good 5.041393 154.68529
## 11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic 1. <=Good 4.318063 75.04315
## 376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic 2. >=Very Good 4.845098 127.11574
## jobclass.1. Industrial jobclass.2. Information health_ins.1. Yes health_ins.2. No
## 231655 1 0 0 1
## 86582 0 1 0 1
## 161300 1 0 1 0
## 155159 0 1 1 0
## 11443 0 1 1 0
## 376662 0 1 1 0
Como comentado acima, nós temos uma variável dummy para cada categoria. Como tínhamos 2 variáveis qualitativas, então ficamos com 4 variáveis dummies. Porém, para um modelo de regressão, isso não é necessário. Estaríamos inserindo 2 variáveis com colinearidade perfeita no modelo: jobclass=industrial é totalmente correlacionada com jobclass=information, pois o resultado de uma influencia totalmente o da outra (o mesmo vale para as variáveis do plano de saúde). Dessa forma, vamos remover essas variáveis desnecessárias.
Wage_dummy = dplyr::select(Wage_dummy, -c("jobclass.2. Information","health_ins.2. No"))
head(Wage_dummy)
## year age maritl race education region health logwage wage
## 231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic 1. <=Good 4.318063 75.04315
## 86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic 2. >=Very Good 4.255273 70.47602
## 161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic 1. <=Good 4.875061 130.98218
## 155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic 2. >=Very Good 5.041393 154.68529
## 11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic 1. <=Good 4.318063 75.04315
## 376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic 2. >=Very Good 4.845098 127.11574
## jobclass.1. Industrial health_ins.1. Yes
## 231655 1 0
## 86582 0 0
## 161300 1 1
## 155159 0 1
## 11443 0 1
## 376662 0 1
Uma maneira mais simples de fazer isso, sem precisarmos retirar cada variável “na mão”, é utilizar o argumento “fullRank=T” da função dummyVars().
dummies = dummyVars(wage~jobclass+health_ins, data = Wage, fullRank = T)
# Aplicando ao modelo:
Dummies = predict(dummies, newdata = Wage)
Note que o comando fullRank=T removeu a primeira variável de cada classificação.
# Anexando esse novo objeto aos dados:
Wage_dummy = cbind(Wage, Dummies)
head(Wage_dummy)
## year age maritl race education region jobclass health health_ins
## 231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic 1. Industrial 1. <=Good 2. No
## 86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic 2. Information 2. >=Very Good 2. No
## 161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic 1. Industrial 1. <=Good 1. Yes
## 155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic 2. Information 2. >=Very Good 1. Yes
## 11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic 2. Information 1. <=Good 1. Yes
## 376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic 2. Information 2. >=Very Good 1. Yes
## logwage wage jobclass.2. Information health_ins.2. No
## 231655 4.318063 75.04315 0 1
## 86582 4.255273 70.47602 1 1
## 161300 4.875061 130.98218 0 0
## 155159 5.041393 154.68529 1 0
## 11443 4.318063 75.04315 1 0
## 376662 4.845098 127.11574 1 0
Variância Zero ou Quase-Zero
Algumas vezes em um conjunto de dados podemos ter uma variável que assuma somente um único valor para todos os indivíduos, ou seja, ela possui variância zero. Ou podemos ter uma com uma frequência muito alta de um único valor, possuindo, assim, variância quase zero. Essas variáveis não auxiliam na predição, pois possuem o mesmo valor em muitos indivíduos, trazendo, assim, pouca informação ao modelo. Nosso objetivo é, então, identificar essas variáveis, chamadas de near zero covariates, para que possamos removê-las do nosso modelo de predição.
Para detectar as near zero covariates, utilizamos a função nearZeroVar() do pacote caret. Vamos verificar se há near zero covariates no banco de dados “forestfires”.
Na função nearZeroVar() passamos primeiro a base de dados a ser analisada, depois o argumento lógico “saveMetrics”, o qual se for “TRUE” retorna todos os detalhes sobre as variáveis da base de dados afim de identificar as near zero covariates. A saída da função fica da seguinte forma:
library(readr)
library(caret)
incendio = read_csv("forestfires.csv")
nearZeroVar(incendio, saveMetrics = T)
## freqRatio percentUnique zeroVar nzv
## X 1.058140 1.740812 FALSE FALSE
## Y 1.624000 1.353965 FALSE FALSE
## month 1.069767 2.321083 FALSE FALSE
## day 1.117647 1.353965 FALSE FALSE
## FFMC 1.000000 20.502901 FALSE FALSE
## DMC 1.111111 41.586074 FALSE FALSE
## DC 1.111111 42.359768 FALSE FALSE
## ISI 1.095238 23.017408 FALSE FALSE
## temp 1.000000 37.137331 FALSE FALSE
## RH 1.375000 14.506770 FALSE FALSE
## wind 1.000000 4.061896 FALSE FALSE
## rain 254.500000 1.353965 FALSE TRUE
## area 82.333333 48.549323 FALSE FALSE
Note que é retornado uma tabela onde nas linhas se encontram as variáveis da base de dados e as colunas podemos resumir da seguinte forma:
-
1ª coluna: a Taxa de Frequência de cada variável. Essa taxa é calculada pela razão de frequências do valor mais comum sobre o segundo valor mais comum.
-
2ª coluna: a Porcentagem de Valores Únicos. Ela é calculada utilizando o número de valores distintos sobre o número de amostras.
-
3ª coluna: indica se a variável tem variância zero.
-
4ª coluna: indica se a variável tem variância quase zero.
Podemos observar que a variável “rain” possui variância quase zero, portanto ela é uma near zero covariate.
hist(incendio$rain, main = "Histograma da Variável Rain",
xlab = "Variável Rain", ylab = "Frequência", col = "purple")
Logo, vamos excluir ela da nossa base de dados. O argumento “saveMetrics=FALSE” (default da função) retorna justamente qual(is) variável(is) do bando de dados é(são) near zero covariate .
nzv = nearZeroVar(incendio)
Nova_incendio = incendio[,-nzv]
head(Nova_incendio)
## # A tibble: 6 x 12
## X Y month day FFMC DMC DC ISI temp RH wind area
## <dbl> <dbl> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 7 5 mar fri 86.2 26.2 94.3 5.1 8.2 51 6.7 0
## 2 7 4 oct tue 90.6 35.4 669. 6.7 18 33 0.9 0
## 3 7 4 oct sat 90.6 43.7 687. 6.7 14.6 33 1.3 0
## 4 8 6 mar fri 91.7 33.3 77.5 9 8.3 97 4 0
## 5 8 6 mar sun 89.3 51.3 102. 9.6 11.4 99 1.8 0
## 6 8 6 aug sun 92.3 85.3 488 14.7 22.2 29 5.4 0
Análise de Componentes Principais (PCA)
Muitas vezes podemos ter variáveis em excesso no nosso banco de dados, o que torna difícil a manipulação das mesmas. A ideia geral do PCA (Principal Components Analysis) é reduzir a quantidade de variáveis, obtendo combinações interpretáveis delas. O PCA faz isso tranformando um conjunto de observações de variáveis possivelmente correlacionadas num conjunto de valores de variáveis linearmente não correlacionadas, chamadas de componentes principais. O número de componentes principais é sempre menor ou igual ao número de variáveis originais, e eles são selecionados de forma que expliquem uma alta porcentagem da variância do modelo.
Para utilizarmos o PCA no nosso modelo, basta colocar o argumento preProcess=“pca” na função train(). Por padrão, são selecionadas componentes que expliquem 95% da variância.
Vamos aplicar o método “glm”, com a opção “pca”, no banco de dados spam.
library(caret)
library(kernlab)
data(spam)
# Criando amostras treino/teste.
set.seed(36)
noTreino = createDataPartition(spam$type, p=0.75, list=F)
treino = spam[noTreino,]
teste = spam[-noTreino,]
Agora vamos treinar o nosso modelo com o PCA.
set.seed(887)
modelo = caret::train(type ~ ., method = "glm", preProcess = "pca", data = treino)
# Aplicando o modelo na amostra TESTE:
testePCA = predict(modelo, teste)
Avaliando nosso modelo com a matriz de confusão:
confusionMatrix(teste$type, testePCA)
## Confusion Matrix and Statistics
##
## Reference
## Prediction nonspam spam
## nonspam 653 44
## spam 56 397
##
## Accuracy : 0.913
## 95% CI : (0.8952, 0.9287)
## No Information Rate : 0.6165
## P-Value [Acc > NIR] : <0.0000000000000002
##
## Kappa : 0.817
##
## Mcnemar's Test P-Value : 0.2713
##
## Sensitivity : 0.9210
## Specificity : 0.9002
## Pos Pred Value : 0.9369
## Neg Pred Value : 0.8764
## Prevalence : 0.6165
## Detection Rate : 0.5678
## Detection Prevalence : 0.6061
## Balanced Accuracy : 0.9106
##
## 'Positive' Class : nonspam
##
O modelo obteve uma acurácia de 0,93, o que pode-se considerar uma alta taxa de acerto.
É possível alterar a porcentagem de variância a ser explicada pelos componentes nas opções do train().
Por exemplo, vamos alterar a porcentagem da variância para 60%.
controle = trainControl(preProcOptions = list(thresh = 0.6))
# Treinando o modelo 2:
set.seed(754)
modelo2 = caret::train(type ~ ., method = "glm", preProcess = "pca", data = treino, trControl = controle)
# Aplicando o modelo 2:
testePCA2 = predict(modelo2, teste)
Avaliando o segundo modelo pela matriz de confusão:
confusionMatrix(teste$type,testePCA2)
## Confusion Matrix and Statistics
##
## Reference
## Prediction nonspam spam
## nonspam 647 50
## spam 71 382
##
## Accuracy : 0.8948
## 95% CI : (0.8756, 0.9119)
## No Information Rate : 0.6243
## P-Value [Acc > NIR] : < 0.0000000000000002
##
## Kappa : 0.7778
##
## Mcnemar's Test P-Value : 0.06904
##
## Sensitivity : 0.9011
## Specificity : 0.8843
## Pos Pred Value : 0.9283
## Neg Pred Value : 0.8433
## Prevalence : 0.6243
## Detection Rate : 0.5626
## Detection Prevalence : 0.6061
## Balanced Accuracy : 0.8927
##
## 'Positive' Class : nonspam
##
Obtemos uma acurácia de 0,92, o que indica também uma alta taxa de acerto, porém um pouco menor que a do modelo anterior. Note que a sensitividade e a especificidade também diminuíram.
Em geral, são utilizados pontos de corte para a variãncia explicada acima de 0,9.
PCA fora da função train()
Podemos também realizar o pré-processamento fora da função train(). Primeiramente vamos criar o pré-processamento, utilizando a amostra treino.
PCA = preProcess(treino, method = c("center","scale","pca"), thresh = 0.95)
Obs: pode-se fixar o número de componentes, utilizando o argumento “pcaComp” ao invés de “thresh”.
Agora aplicamos o pré-processamento na amostra treino e realizamos o treinamento, utilizando a amostra treino já pré-processada.
treinoPCA = predict(PCA, treino)
modelo = caret::train(type ~ ., data = treinoPCA, method="glm")
Aplicando o pré-processamento na amostra teste:
testePCA = predict(PCA, teste)
Por último, aplicamos o modelo criado com a amostra treino na amostra teste pré-processada.
testeMod = predict(modelo, testePCA)
# Avaliando o modelo:
confusionMatrix(testePCA$type, testeMod)
## Confusion Matrix and Statistics
##
## Reference
## Prediction nonspam spam
## nonspam 653 44
## spam 56 397
##
## Accuracy : 0.913
## 95% CI : (0.8952, 0.9287)
## No Information Rate : 0.6165
## P-Value [Acc > NIR] : <0.0000000000000002
##
## Kappa : 0.817
##
## Mcnemar's Test P-Value : 0.2713
##
## Sensitivity : 0.9210
## Specificity : 0.9002
## Pos Pred Value : 0.9369
## Neg Pred Value : 0.8764
## Prevalence : 0.6165
## Detection Rate : 0.5678
## Detection Prevalence : 0.6061
## Balanced Accuracy : 0.9106
##
## 'Positive' Class : nonspam
##
Normalização dos Dados
Transformação de Box-Cox
A transformação de Box-Cox é uma transformação feita nos dados (contínuos) para tentar normalizá-los. Considerando $X_1,…,X_n$ as variáveis do conjunto de dados original, essa transformação consiste em encontrar um $\lambda$ tal que as variáveis transformadas $Y_1,…Y_n$ se aproximem de uma distribuição normal com variância constante.
Essa transformação é dada pela seguinte forma: \(Y_i(\lambda)=\frac{X_i^{\lambda}-1}{\lambda} \hbox{ , se } \lambda \neq 0.\) O parâmetro $\lambda$ é estimado utilizando o método de máxima verossimilhança.
O método de Box-Cox é o método mais simples e o mais eficiente computacionalmente. Podemos aplicar a transformação de Box-Cox nos dados através da função preProcess().
OBS: a transformação de Box-Cox só pode ser utilizada com dados positivos.
treinoBC = preProcess(treino, method = "BoxCox")
Outras Transformações
Transformação de Yeo-Johnson
A transformação de Yeo-Johnson é semelhante à transformação de Box-Cox, porém ela aceita preditores com dados nulos e/ou dados negativos. Também podemos aplicá-la aos dados através da função preProcess().
treinoYJ = preProcess(treino, method = "YeoJohnson")
Transformação Exponencial de Manly
O método exponencial de Manly também consiste em estimar um $\lambda$ tal que as variáveis transformadas se aproximem de uma distribuição normal. Assim como a transformação de Yeo-Johnson, ela também aceita dados positivos, nulos e negativos. Essa transformação é dada pela seguinte forma: \(Y_i(\lambda)=\frac{e^{X\lambda}-1}{\lambda} \hbox{ , se } \lambda \neq 0.\)
treinoEXP = preProcess(treino, method = "expoTrans")
Métodos de Treino Baseados em Árvores
Neste capítulo será estudado de forma mais aprofundada modelos de treinamento baseados em árvores, os quais são simples para interpretação, como: árvores de decisão e regressão, florestas aleatórias, adaboost, entre outros. O objetivo é entender o funcionamento dos mesmos, assim como os critérios que utilizam para classificarem as amostras.
É importante deixar claro que para utilizarmos esses métodos podemos usar tanto dados numéricos quanto categóricos. Além disso, não é necessário padronizar os dados.
Árvores de Decisão
Uma árvore de decisão, em geral, pergunta uma questão e classifica o elemento baseado na resposta. Ela utiliza os dados de cada indivíduo para criar uma regra de separação, que posteriormente será utilizada para rotular novas amostras.
As árvores de decisão podem ser aplicadas aos problemas de regressão e classificação. Primeiro vamos considerar os problemas de classificação, e depois passamos para a regressão.
em Classificação
Vejamos a seguir um exemplo de árvore de decisão para um problema de classificação.
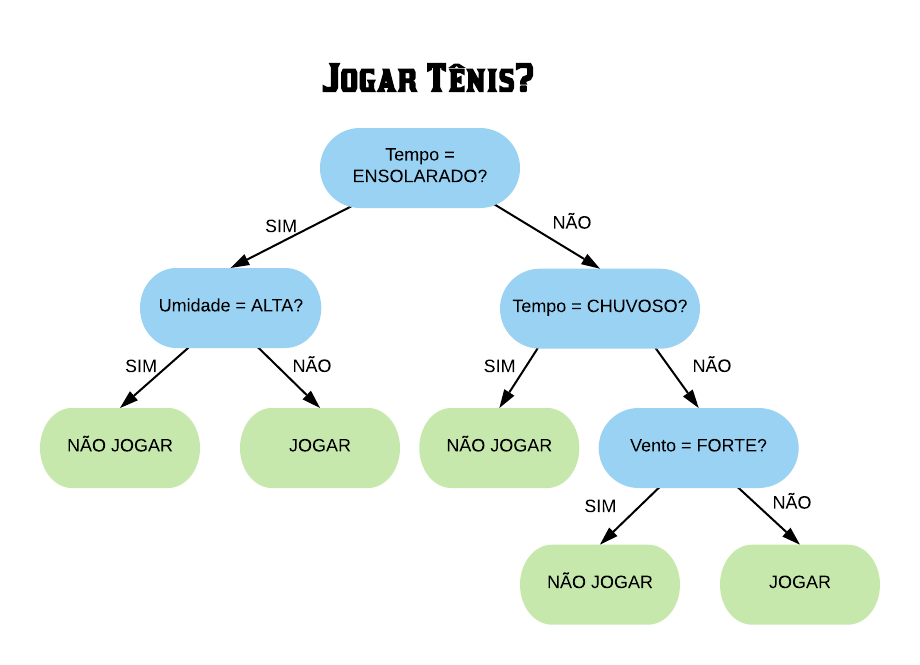
Nomenclatura:
- Nó Raiz ou Raiz: é a variável que se encontra no topo da árvore;
- Nós Internos ou Nós: são as variáveis intermediárias, que possuem tanto setas apontandas para elas como saindo delas;
- Nós Folhas ou Nós Terminais ou Folhas: possuem apenas setas apontadas para elas. Representam a decisão final da árvore.
No processo de construção de uma árvore de decisão é importante ressaltar que a separação dos dados deve envolver apenas duas respostas: “Sim” ou “Não”. Também é preciso definir a ordem das variáveis, como a variável com que se deve começar, qual deve ser a seguinte, e assim por diante. A solução para isso é obtida através do nível de impureza das variáveis.
Dizemos que uma variável é impura quando ela não consegue separar bem os dados em uma árvore de decisão. Para calcularmos a impureza de uma variável utilizamos o indíce Gini, que varia entre 0 (mais puro possível) e 0,5 (mais impuro possível). Primeiramente calculamos o índice Gini para cada nó da variável, e em seguida obtemos o índice Gini da variável como uma média ponderada. O índice Gini de um nó é obtido por: \(\hbox{Gini(nó)} = 1 - {p_S}^{2} - {p_N}^{2}.\) onde $p_S$ é a proporção de “sim” da resposta da variável de interesse e $p_N$ a proporção de “não” da resposta da variável de interesse.
O índice Gini da variável é dado pela média do índice Gini para os nós referentes às respostas “Sim” e “Não” ponderada pela proporção dos elementos em cada nó.
\[\hbox{Gini(variável)} = \hbox{Gini(nó}_1) \times P_1 + \hbox{Gini(nó}_2) \times P_2\]onde $P_1$ é a proporção de elementos no 1º nó e $P_2$ é a proporção de elementos no 2º nó.
Vamos construir uma árvore de decisão utilizando a base SmallHeart.
base = readRDS("SmallHeart.rds")
head(base)
## # A tibble: 6 x 4
## Sex ChestPain Thal HeartDisease
## <fct> <chr> <chr> <chr>
## 1 M typical fixed No
## 2 F nontypical normal No
## 3 M nontypical normal No
## 4 F nontypical normal No
## 5 M nontypical reversable No
## 6 M nontypical reversable Yes
Nosso objetivo é prever se um indivíduo tem ou não uma doença cardíaca (variável “HeartDisease”), baseado nas outras variáveis. As variáveis explicativas são as seguintes:
- Sex: indica o sexo do indivíduo, onde “M” = Masculino e “F” = Feminino;
- ChestPain: referente ao indivíduo sentir dor no peito, onde “typical” = típico e “nontypical” = não típico;
- Thal: indica se o indivíduo possui Talassemia, onde “normal” = não possui, “fixed” = talassemia irreversível e “reversable” = talassemia reversível.
Vamos verificar o quão bem as variáveis isoladamente são capazes de prever se o paciente possui ou não doença cardíaca. Vamos começar pela variável “Sex”.
summary(base$Sex)
## F M
## 22 50
Note que temos 22 indivíduos do sexo feminino e 50 indivíduos do sexo masculino. Como a resposta de um nó da árvore deve ser “Sim” ou “Não”, vamos utilizar a variável “Sex=M”.
# Verificando quantos indivíduos possuem doença cardíaca de acordo com o sexo:
base %>% group_by(Sex, HeartDisease) %>% summarise(N=n())
## # A tibble: 4 x 3
## # Groups: Sex [2]
## Sex HeartDisease N
## <fct> <chr> <int>
## 1 F No 20
## 2 F Yes 2
## 3 M No 36
## 4 M Yes 14
Então a variável “Sex=M” separa os pacientes da seguinte forma:
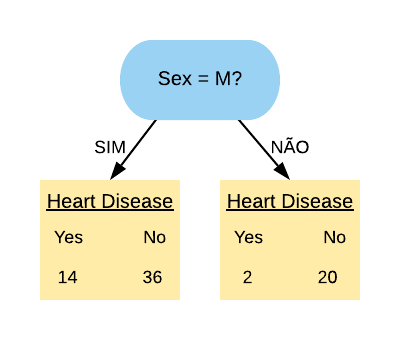
Note que a maioria dos pacientes com doença cardíaca terminaram na folha referente ao sexo masculino, mas a maioria dos que não possuem doença também. Já podemos ter uma ideia que essa variável não é tão boa em separar os dados, mas para averiguarmos essa hipótese vamos calcular o índice gini dela.
Primeiramente vamos calcular o índice Gini do nó “Sex = M Sim”:
\[\hbox{Gini(Sex = M Sim)} = 1- \left( \frac{14}{50} \right)^{2} - \left( \frac{36}{50} \right)^{2} = 0,403.\]Agora vamos calcular o índice Gini do nó “Sex = M Não”:
\[\hbox{Gini(Sex = M Não)} = 1- \left( \frac{2}{22} \right)^{2} - \left( \frac{20}{22} \right)^{2} = 0,166.\]O índice Gini da variável “Sex = M” é dado pela média do índice Gini dos nós referentes às respostas “Sim” e “Não” ponderada pela frequência dos indivíduos em cada nó.
\[\hbox{Gini(Sex = M)} = 0,403 \times \frac{50}{72} + 0,166 \times \frac{22}{72} = 0,331.\]Como o índice Gini da variável “Sex = M” ficou mais próximo de 0,5 do que de 0, podemos constatar que ela é uma variável com baixa pureza. Note que se tivéssemos escolhido a variável “Sex = F” o índice Gini obtido seria o mesmo, pois “Sex = F Sim” é equivalente a “Sex = M Não” e “Sex = F Não” é equivalente a “Sex = M Sim”. ou seja, as contas seriam as mesmas.
Agora vamos realizar o mesmo processo para a variável “ChestPain”, ou seja, vamos verificar o quão bem ela é capaz de prever se o paciente possui doença cardíaca.
base %>% group_by(ChestPain) %>% summarise(N=n())
## # A tibble: 2 x 2
## ChestPain N
## <chr> <int>
## 1 nontypical 49
## 2 typical 23
Note que temos 23 indivíduos que sentem dor no peito tipicamente e 49 indivíduos que não sentem tipicamente. Vamos verificar quantos deles possuem doença cardíaca:
base %>% group_by(ChestPain, HeartDisease) %>% summarise(N=n())
## # A tibble: 4 x 3
## # Groups: ChestPain [2]
## ChestPain HeartDisease N
## <chr> <chr> <int>
## 1 nontypical No 40
## 2 nontypical Yes 9
## 3 typical No 16
## 4 typical Yes 7
Vamos considerar a variável “ChestPain = Typical”. Ela separa os dados da seguinte forma:
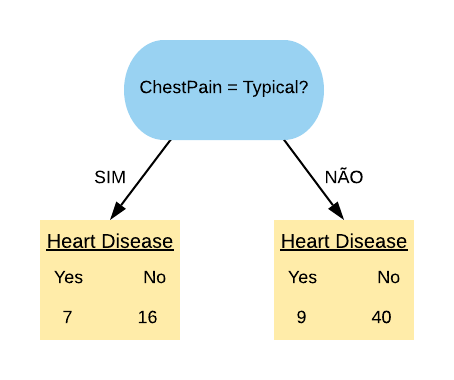
Note que quase metade dos pacientes que possuem dor no peito têm doença cardíaca. Dos que não sentem a dor no peito, quase $\frac{1}{4}$ apenas possui a doença.
Vamos calcular o índice Gini do nó “ChestPain = Typical Sim”:
\[\hbox{Gini(ChestPain = Typical Sim)} = 1- \left( \frac{7}{23} \right)^{2} - \left( \frac{16}{23} \right)^{2} = 0,423.\]Agora vamos calcular o índice Gini do nó “ChestPain = Typical Não”:
\[\hbox{Gini(ChestPain = Typical Não)} = 1- \left( \frac{9}{49} \right)^{2} - \left( \frac{40}{49} \right)^{2} = 0,299.\]O índice Gini da variável “ChestPain = Typical” é dado pela média do índice Gini dos nós referentes às respostas “Sim” e “Não” ponderada pela frequência dos indivíduos em cada nó.
\[\hbox{Gini(ChestPain = Typical)} = 0,423 \times \frac{23}{72} + 0,299 \times \frac{49}{72} = 0,339.\]Note que ela obteve um índice Gini um pouco maior do que a variável “Sex = M”. Isso indica que a variável “Sex = M” é mais pura do que a variável “ChestPain = Typical”.
Agora falta apenas obter o índice Gini da variável “Thal”. Mas diferentemente das outras 2 ela não possui apenas 2 níveis, e sim 3: “normal”, “fixed” e “reversable”.
library(dplyr)
base %>% group_by(Thal) %>% summarise(N=n())
## # A tibble: 3 x 2
## Thal N
## <chr> <int>
## 1 fixed 4
## 2 normal 52
## 3 reversable 16
Nesse caso vamos ter que calcular o índice Gini para todas as combinações possíveis: “Thal = normal”, “Thal = fixed”, “Thal = reversable”, “Thal = normal ou fixed”, “Thal = normal ou reversable”, “Thal = fixed ou reversable”. Porém note que o índice Gini da variável “Thal = normal” é equivalente ao da variável “Thal = fixed ou reversable”, pois “Thal = normal Sim” é o mesmo que “Thal = fixed ou reversable Não”. Da mesma forma isso vale para as variáveis “Thal = fixed” e “Thal = normal ou reversable”, e “Thal = reversable” e “Thal = normal ou fixed”. Com isso conseguimos economizar algumas contas.
base %>% group_by(Thal, HeartDisease) %>% summarise(N=n())
## # A tibble: 6 x 3
## # Groups: Thal [3]
## Thal HeartDisease N
## <chr> <chr> <int>
## 1 fixed No 3
## 2 fixed Yes 1
## 3 normal No 44
## 4 normal Yes 8
## 5 reversable No 9
## 6 reversable Yes 7
Vamos, primeiramente, olhar para a variável “Thal = normal”. Ela separa os dados da seguinte forma:
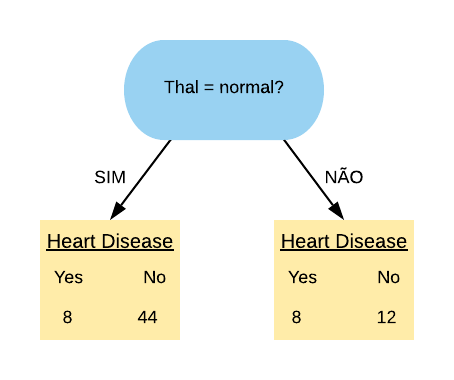
Note que a maioria dos pacientes que possuem doença cardíaca estão no grupo dos que possuem “Thal = normal”.
Vamos calcular o índice Gini do nó “Thal = Normal Sim”:
\[\hbox{Gini(Thal = Normal Sim)} = 1- \left( \frac{8}{52} \right)^{2} - \left( \frac{44}{52} \right)^{2} = 0,26.\]Agora vamos calcular o índice Gini do nó “Thal = Normal Não”:
\[\hbox{Gini(Thal = Normal Não)} = 1- \left( \frac{8}{20} \right)^{2} - \left( \frac{12}{20} \right)^{2} = 0,48.\]Então o índice Gini da variável “Thal = Normal” fica da seguinte forma:
\[\hbox{Gini(Thal = Normal)} = 0,26 \times \frac{52}{72} + 0,48 \times \frac{20}{72} = 0,321.\]Agora vamos olhar para a variável “Thal = Fixed”. Ela separa os dados da seguinte forma:
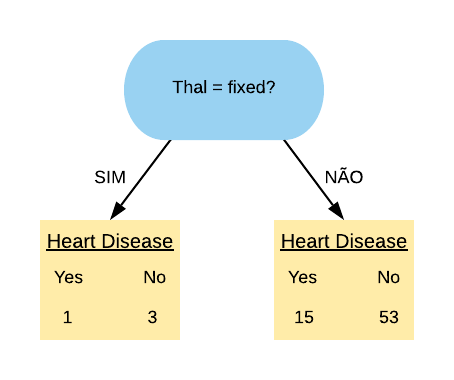
Vamos calcular o índice Gini do nó “Thal = Fixed Sim”:
\[\hbox{Gini(Thal = Fixed Sim)} = 1- \left( \frac{1}{4} \right)^{2} - \left( \frac{3}{4} \right)^{2} = 0,375.\]Agora vamos calcular o índice Gini do nó “Thal = Fixed Não”:
\[\hbox{Gini(Thal = Fixed Não)} = 1- \left( \frac{15}{68} \right)^{2} - \left( \frac{53}{68} \right)^{2} = 0,344.\]Então o índice Gini da variável “Thal = Fixed” fica da seguinte forma:
\[\hbox{Gini(Thal = Fixed)} = 0,375 \times \frac{4}{72} + 0,344 \times \frac{68}{72} = 0,346.\]Por último, vamos olhar para a variável “Thal = Reversable”.
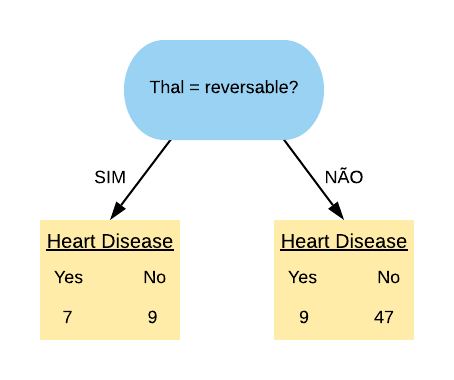
Vamos calcular o índice Gini do nó “Thal = Reversable Sim”:
\[\hbox{Gini(Thal = Reversable Sim)} = 1- \left( \frac{7}{16} \right)^{2} - \left( \frac{9}{16} \right)^{2} = 0,492.\]Agora vamos calcular o índice Gini do nó “Thal = Reversable Não”:
\[\hbox{Gini(Thal = Reversable Não)} = 1- \left( \frac{9}{56} \right)^{2} - \left( \frac{47}{56} \right)^{2} = 0,269.\]Então o índice Gini da variável “Thal = Reversable” fica da seguinte forma:
\[\hbox{Gini(Thal = Reversable)} = 0,492 \times \frac{16}{72} + 0,269 \times \frac{56}{72} = 0,319\]Resumindo, os índices Ginis de todas as variáveis são:
| Variáveis | Índice Gini |
|---|---|
| Sex = M | 0,331 |
| ChestPain = Typical | 0,339 |
| Thal = Normal | 0,321 |
| Thal = Fixed | 0,346 |
| Thal = Reversable | 0,319 |
A variável “Thal = Reversable” é a que possui o menor índice Gini, portanto ela é a mais pura. Ela ficará no topo da árvore de decisão, ou seja, será o nó raiz.
O próximo passo é definir as variáveis que ficarão no nó “Thal = Reversable Sim” e “Thal = Reversable Não”. Para isso temos que olhar para a base de dados com os indivíduos do grupo “Thal = Reversable Sim” e “Thal = Reversable Não”, respectivamente.
# Grupo de indivíduos "Thal = Reversable Sim":
base1 = base %>% filter(Thal == "reversable")
head(base1)
## # A tibble: 6 x 4
## Sex ChestPain Thal HeartDisease
## <fct> <chr> <chr> <chr>
## 1 M nontypical reversable No
## 2 M nontypical reversable Yes
## 3 M typical reversable No
## 4 M nontypical reversable No
## 5 M nontypical reversable Yes
## 6 M typical reversable Yes
Agora temos que calcular o índice Gini para todas as variáveis referentes a esse grupo. A que for mais pura entrará no nó “Thal = Reversable Sim”. Poupando os cálculos, vamos obter que o menor índice Gini é o da variável “ChestPain = Typical”.
# Grupo de indivíduos "Thal = Reversable Não":
base2 = base %>% filter(Thal != "reversable")
head(base2)
## # A tibble: 6 x 4
## Sex ChestPain Thal HeartDisease
## <fct> <chr> <chr> <chr>
## 1 M typical fixed No
## 2 F nontypical normal No
## 3 M nontypical normal No
## 4 F nontypical normal No
## 5 M nontypical normal No
## 6 M typical normal No
Agora calculamos também o índice Gini para todas as variáveis referentes a esse grupo. Após os cálculos necessários veremos que o menor índice Gini é o da variável “ChestPain = Nontypical”.
Dessa forma, podemos dar continuidade a nossa árvore.
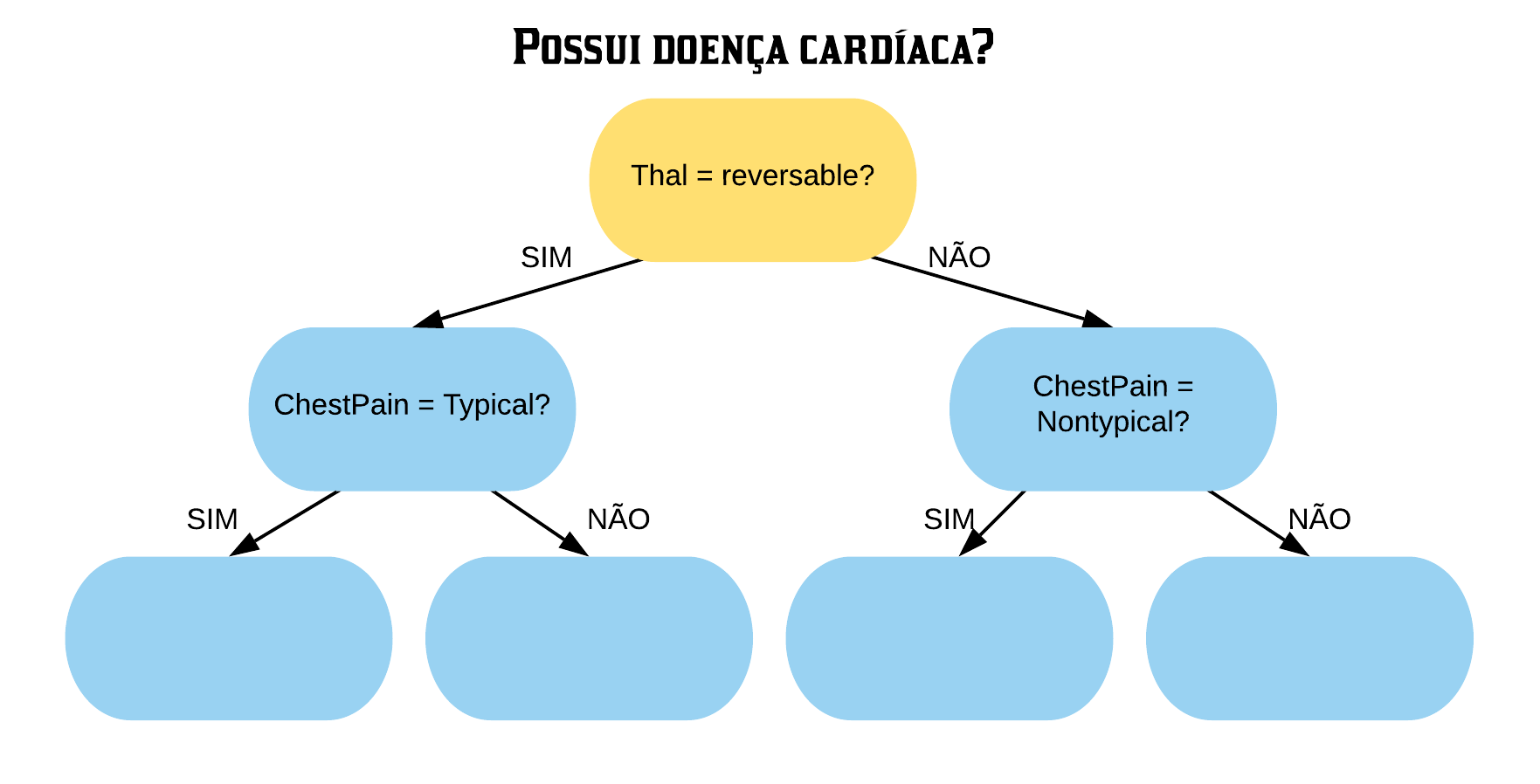
Após obtidos esses novos nós, o processo continua se repetindo, obtendo novos nós e/ou folhas para a árvore, até a construção chegar ao fim.
Pergunta: quando o processo de construção de uma árvore chega ao fim? O processo de construção pode terminar por 3 fatores:
-
Quando a pureza do nó é maior do que o de qualquer variável que adicionamos;
-
Quando atingimos folhas 100% puras (índice Gini = 0);
-
Quando o ganho ao aumentar a árvore é muito pequeno.
O ganho ao aumentar a árvore pode ser resumido como um conjunto de atributos presentes na árvore que retornem o maior ganho de informações. Essa questão será melhor abordada posteriormente, juntamente com a questão de como podar as árvores (que está intimamente relacionada ao ganho) no subcapítulo [XGBoost].
em Regressão
Agora iremos discutir o processo de construção de uma árvore de regressão. Em uma árvore de regressão, diferentemente de uma árvore para classificação, cada folha possui um valor numérico (ao invés de categorias como “Sim” ou “Não”, como no exemplo anterior da base SmallHeart). Vejamos a seguir um exemplo de árvore de decisão para um problema de regressão.
Esse valor numérico presente nas folhas não é nada menos que a média do valor da variável de interesse a ser prevista para os elementos que satisfazem a condição do nó. Por exemplo, na árvore de regressão acima a primeira folha dá como resultado uma eficácia de 5%: essa foi a média observada da eficácia do medicamento em pacientes com mais de 50 anos de idade. Para a segunda folha, a com eficácia de 20%: esse valor é a média da eficácia do medicamento em um indivíduo com menos de 50 anos de idade e que toma uma dosagem maior do que 29mg foi de 20%. O processo é o mesmo para as outras folhas.
A grande pergunta é qual valor colocar no nó como condição. Para exemplificar como funciona o processo, vamos começar com um exemplo simples:
Ex.: Vamos carregar o banco de dados “SmallAdvertising”. Este banco possui informações sobre as vendas de um produto em 10 mercados diferentes (variável sales), além de orçamentos de publicidade para esse produto em cada um dos mercados para três mídias diferentes: TV, rádio e jornal (variáveis TV, radio e newspaper, respectivamente).
vendas = readRDS("SmallAdvertising.rds")
vendas
## # A tibble: 11 x 4
## TV radio newspaper sales
## <dbl> <dbl> <dbl> <dbl>
## 1 200. 2.6 21.2 10.6
## 2 66.1 5.8 24.2 8.6
## 3 215. 24 4 17.4
## 4 23.8 35.1 65.9 9.2
## 5 97.5 7.6 7.2 9.7
## 6 204. 32.9 46 19
## 7 195. 47.7 52.9 22.4
## 8 67.8 36.6 114 12.5
## 9 281. 39.6 55.8 24.4
## 10 69.2 20.5 18.3 11.3
## 11 147. 23.9 19.1 14.6
Vamos considerar o caso em que queremos construir uma árvore de regressão para prever as vendas baseados apenas na variável TV.
plot(vendas$TV, vendas$sales, pch = 19,
xlab = "Orçamento de Publicidade do Produto para a TV",
ylab = "Vendas do Produto",
main = "Vendas do produto x Publicidade para a TV")
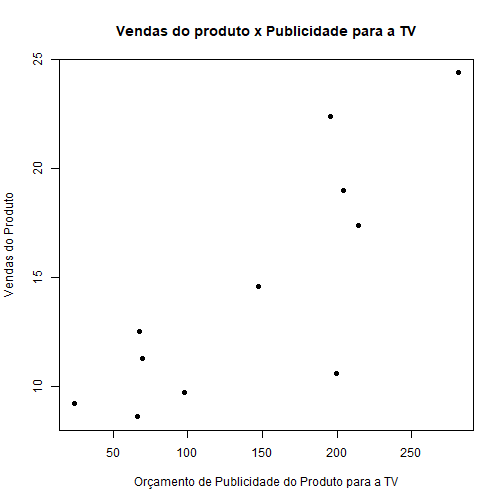
Primeiramente é preciso definir qual valor irá entrar como condição no primeiro nó. O algoritmo realiza isso testando todos os possíveis valores de separação para os dados, e pega o que minimiza a soma dos quadrados dos resíduos. Inicialmente, como o primeiro separador, ele considera a média dos 2 menores valores da Publicidade.
ordenados = sort(vendas$TV)
mean(ordenados[1:2])
## [1] 44.95
Então 44,95 é o primeiro valor a ser testado para a separação dos dados.
plot(vendas$TV, vendas$sales, pch = 19,
xlab = "Orçamento de Publicidade do Produto para a TV",
ylab = "Vendas do Produto",
main = "Vendas do produto x Publicidade para a TV"); abline(v = 44.95,
col = "red")
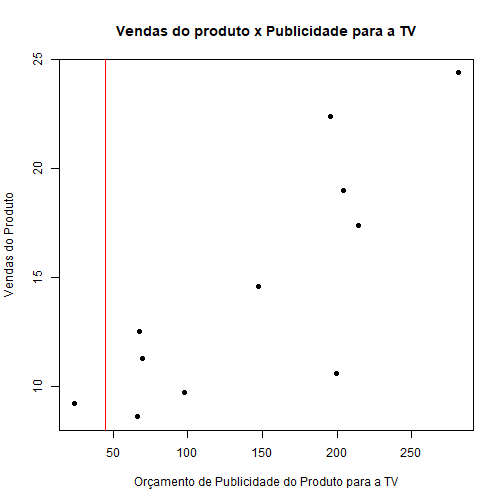
Assim, o primeiro nó será da seguinte forma:
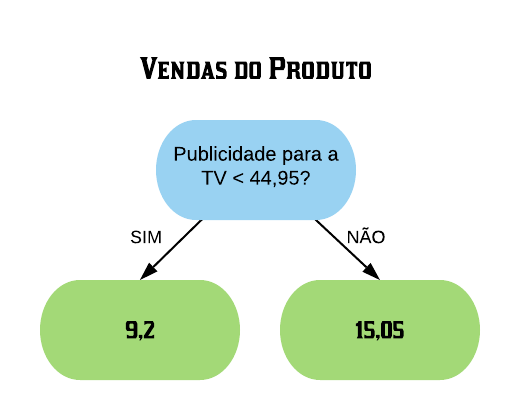
Para a resposta “sim” prevemos que as vendas do produto será de 9,2, o qual é o resultado da média dos valores das vendas para todos os produtos cuja publicidade foi menor do que 44,95 (ou seja, é apenas o valor do primeiro elemento). Para a resposta “Não”, então a folha seguinte contém o resultado da média dos valores das vendas para todos os produtos cuja publicidade foi maior do que 44,95, o qual é de 15,05.
Note que fazendo isso teremos resíduos (diferença do valor original e do valor predito pela árvore) muito grandes. O algoritmo eleva esses resíduos ao quadrado e os soma. Esse valor é a soma dos quadrados dos resíduos considerando o nó “Publicidade para a TV < 44,95?”.
Em seguida ele irá para o próximo separador: a média do segundo e do terceiro menores pontos.
mean(ordenados[2:3])
## [1] 66.95
Então 66,95 é o segundo valor a ser testado para a separação dos dados.
plot(vendas$TV, vendas$sales, pch = 19,
xlab = "Orçamento de Publicidade do Produto para a TV",
ylab = "Vendas do Produto",
main = "Vendas do produto x Publicidade para a TV"); abline(v = 66.95,
col = "red")
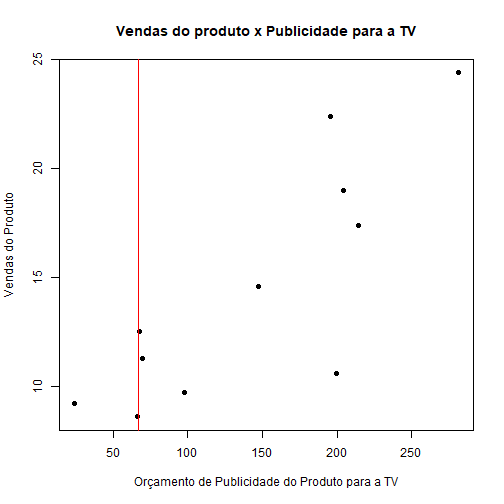
Então o nó considerado será da forma “Publicidade para a TV < 66,95?”.
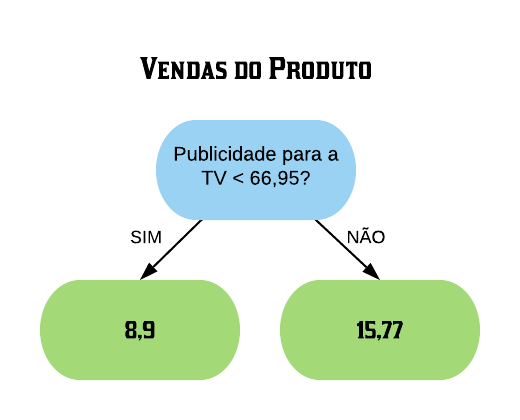
O valor de 8,9 corresponde ao resultado da média dos valores das vendas para todos os produtos cuja publicidade foi menor do que 66,95. Então a árvore prevê esse valor de vendas para o produto que obteve uma publicidade para a TV < 66,95. O valor de 15,77 é o resultado da média dos valores das vendas para todos os produtos cuja publicidade foi maior do que 66,95. Novamente serão obtidos os resíduos dessa predição e eles serão somados.
Então o algoritmo irá para o próximo separador e irá calcular a soma dos quadrados dos resíduos da predição. Isso ocorre sucessivamente até acabarem todos os separadores possíveis para a árvore. O separador vencedor (aquele que irá para o nó raiz) é aquele com a menor soma dos quadrados dos resíduos.
A construção dos próximos nós se dá pela mesma forma que a do nó raiz. O processo de construção da árvore termina quando:
- Atingimos um número mínimo de observações em uma folha (usualmente é utilizado 20 observações). Não continuamos a divisão após esse número mínimo pois corremos o risco de criar uma árvore sobreajustada à amostra dada;
- Quando o ganho ao aumentar a árvore é muito pequeno.
Agora vamos para o caso em que tenhamos mais de uma variável preditiva nos dados. Vamos considerar agora que queremos prever as vendas do produto baseado em seus orçamentos de publicidade para TV, rádio e jornal.
Assim como anteriormente, começamos usando o orçamento para a TV para prever as vendas, e pegamos o separador com a menor soma dos quadrados dos resíduos. O melhor separador se torna um candidato para a raiz da árvore. Em seguida, focamos em utilizar o orçamento para o rádio para prever as vendas. Assim como com o orçamento para a TV, tentamos diferentes separadores para a predição e calculamos a soma dos quadrados dos resíduos em cada passo. O melhor separador se torna outro candidato para a raiz. Por último, utilizamos o orçamento para o jornal para prever as vendas, e após tentarmos diferentes separadores pegamos aquele com a menor soma dos quadrados dos resíduos também. Então comparamos a soma dos quadrados dos resíduos de todos os candidatos para a raiz, e o escolhido, novamente, é aquele com a menor soma.
Para os próximos nós o processo de construção também é equivalente ao anterior, exceto que agora nós comparamos a menor soma dos quadrados dos resíduos de cada preditor. E, novamente, quando uma folha atinge um número mínimo de observações, a árvore é finalizada.
Construindo árvores com o rpart e rpart.plot
Vamos construir árvores com o comando rpart(). Como argumento da função nós passamos:
- A variável de interesse a ser prevista em função das variáveis preditoras;
- A base de dados onde as variáveis se encontram.
Vamos utilizar a base de dados referentes ao primeiro exemplo dado de construção de uma árvore, onde queríamos prever se um indivíduo possui doença cardíaca baseado em características dele.
library(rpart)
heart_arvore = rpart(HeartDisease~., data = base)
Agora vamos plotar a árvore com o comando rpart.plot().
library(rpart.plot)
rpart.plot(heart_arvore)

Observe que a árvore ficou “vazia”. O que ela quer dizer com isso é: assuma “Não” sempre para o indivíduo possuir doença cardíaca, e acerte com precisão de 78%. Isso ocorre devido aos valores iniciais do comando rpart.control(), que ajusta os parâmetros da função rpart(). Os principais parâmetros do rpart.control são:
-
minsplit: o número mínimo de observações que devem existir em um nó para que uma divisão seja tentada. Padrão: minsplit = 20;
-
minbucket: o número mínimo de observações em qualquer folha. Padrão: minbucket = minsplit/3;
-
cp (complexity parameter): o mínimo de ganho de ajuste que devemos ter em cada divisão. O principal papel desse parâmetro é economizar tempo de computação removendo as divisões que não valem a pena. Padrão: cp = 0,01;
-
maxdepth: profundidade máxima da árvore (a profundidade da raiz é zero). Não pode ser maior que 30.
Ex. 1: Vamos ajustar os parâmetros da árvore e construí-la novamente. Vamos determinar que a profundidade da árvore seja 2, que 0 seja o número mínimo de observações em um nó e que ela seja construída mesmo que não haja ganhos em mais divisões.
controle = rpart.control(minsplit=0, cp = -1, maxdepth = 2)
heart_arvore = rpart(HeartDisease~., data = base, control = controle)
rpart.plot(heart_arvore)
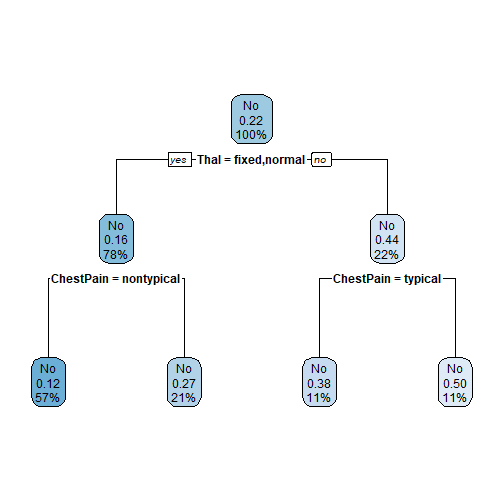
Note que o nó raiz é exatamente aquele que calculamos como o mais puro, o “Thal = Reversable”, que é equivalente a “Thal = Fixed ou Normal”. Os nós adjacentes também foram o que obtivemos anteriormente como os mais puros.
Cada saída do comando rpart.plot() tem um significado específico:
- A primeira saída é a classe estimada pela árvore para as amostras que se encontram naquele nó.
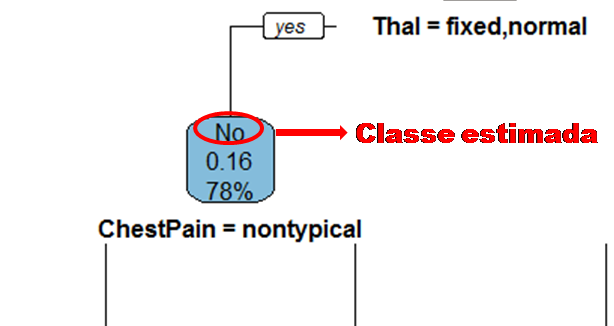
- A segunda saída é a proporção de indivíduos na classe contrária àquela estimada na primeira saída.

- A terceira saída é a porcentagem da amostra que se encontra no atual nó.
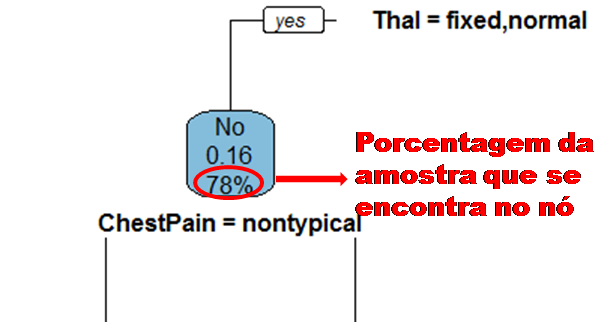
Ex. 2: Vamos agora constuir a árvore mais completa possível, ou seja, uma árvore sobreajustada à amostra, sem restrições em sua profundidade máxima.
controle = rpart.control(minsplit=0, cp = -1)
heart_arvore = rpart(HeartDisease~., data = base, control = controle)
rpart.plot(heart_arvore)
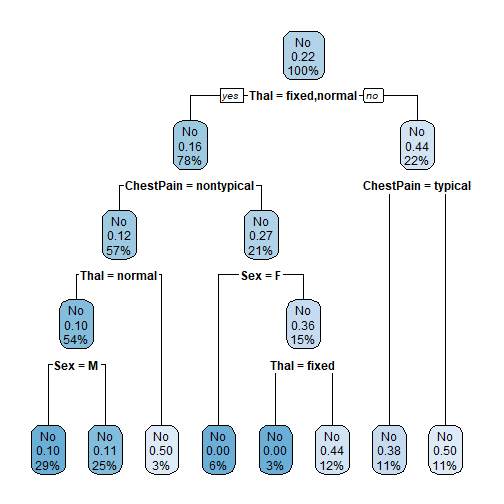
Ex. 3: Vamos agora considerar 10 como o número mínimo de observações em um nó e 3 como a profundidade máxima da árvore.
controle = rpart.control(minsplit=10, cp = -1, maxdepth = 4)
heart_arvore = rpart(HeartDisease~., data = base, control = controle)
rpart.plot(heart_arvore)
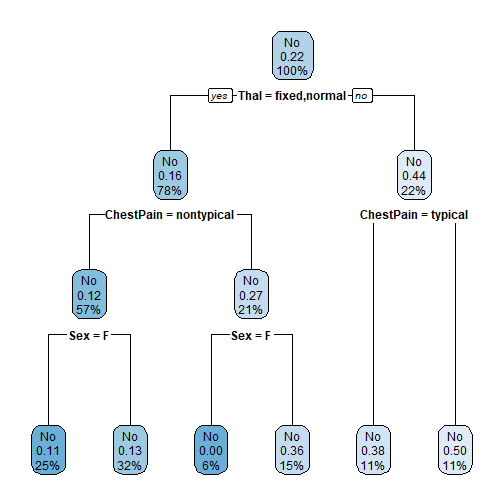
Agora podemos levantar a seguinte questão: como avaliar a precisão do modelo construído? Nesse exemplo nós utilizamos toda a amostra para construir a árvore, apenas para explicar o funcionamente do rpart, então não temos uma amostra teste para verificar o quão bom é o modelo. Então para isso teríamos que primeiramente dividir a amostra em treino e teste, depois criar o modelo com a amostra treino e em seguida aplicá-lo na amostra teste, e então, por último, poderíamos utilizar a função confusionMatrix() para obtermos não só a precisão como outras medidas avaliativas do modelo, além, é claro, da matriz de confusão. No tópico abaixo essas etapas serão construídas detalhadamente.
Construindo árvores com train
Podemos utilizar árvores de decisão/regressão como um método de treinamento para os dados através da função train(). Vamos fazer isso utilizando a base de dados College. Este banco possui informações sobre 777 diferentes universidades e faculdades dos EUA. Ela apresenta algumas variáveis como: Apps - número de pedidos recebidos para ingresso, Room.Board - custos de acomodação e alimentação, Books - custos estimados de livros, PhD - quantidade de professores com doutorado, entre outras, e nossa variável de interesse Private, que indica se a universidade é privada ou pública.
library(readr)
college = read_csv2("College.csv")
head(college)
## # A tibble: 6 x 18
## Private Apps Accept Enroll Top10perc Top25perc F.Undergrad P.Undergrad Outstate Room.Board Books Personal PhD
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Yes 1660 1232 721 23 52 2885 537 7440 3300 450 2200 70
## 2 Yes 2186 1924 512 16 29 2683 1227 12280 6450 750 1500 29
## 3 Yes 1428 1097 336 22 50 1036 99 11250 3750 400 1165 53
## 4 Yes 417 349 137 60 89 510 63 12960 5450 450 875 92
## 5 Yes 193 146 55 16 44 249 869 7560 4120 800 1500 76
## 6 Yes 587 479 158 38 62 678 41 13500 3335 500 675 67
## # ... with 5 more variables: Terminal <dbl>, S.F.Ratio <dbl>, perc.alumni <dbl>, Expend <dbl>, Grad.Rate <dbl>
Vamos, primeiramente, separar a amostra em treino e teste.
library(caret)
set.seed(100)
noTreino = createDataPartition(y = college$Private, p = 0.7, list = F)
treino = college[noTreino,]
teste = college[-noTreino,]
Vamos treinar o modelo pelo método de árvores de decisão. Fazemos isso através do argumento “method = rpart” da função train().
set.seed(100)
modelo = caret::train(Private~., method = "rpart", data = treino)
modelo
## CART
##
## 545 samples
## 17 predictor
## 2 classes: 'No', 'Yes'
##
## No pre-processing
## Resampling: Bootstrapped (25 reps)
## Summary of sample sizes: 545, 545, 545, 545, 545, 545, ...
## Resampling results across tuning parameters:
##
## cp Accuracy Kappa
## 0.04362416 0.9081649 0.7588635
## 0.20134228 0.8721337 0.6609327
## 0.51006711 0.8325440 0.5238781
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was cp = 0.04362416.
Observe que através do train() são testados alguns valores para o cp (complexity parameter) e é eleito aquele com a maior taxa de acurácia. Nesse caso, o cp utilizado será o de aproximadamente 0,0436. Vamos aplicar o modelo no conjunto teste.
predicao = predict(modelo, teste)
# Transformando em fator para depois construirmos a matriz de confusão:
teste$Private = as.factor(teste$Private)
# Avaliando o modelo utilizando a matriz de confusão:
confusionMatrix(predicao, teste$Private)
## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 44 6
## Yes 19 163
##
## Accuracy : 0.8922
## 95% CI : (0.845, 0.929)
## No Information Rate : 0.7284
## P-Value [Acc > NIR] : 0.0000000007796
##
## Kappa : 0.7088
##
## Mcnemar's Test P-Value : 0.0164
##
## Sensitivity : 0.6984
## Specificity : 0.9645
## Pos Pred Value : 0.8800
## Neg Pred Value : 0.8956
## Prevalence : 0.2716
## Detection Rate : 0.1897
## Detection Prevalence : 0.2155
## Balanced Accuracy : 0.8315
##
## 'Positive' Class : No
##
Obtivemos uma acurácia de 0,8922, o que é razoável para um modelo que utiliza árvores.
# Desenhando a árvore:
rpart.plot(modelo$finalModel)
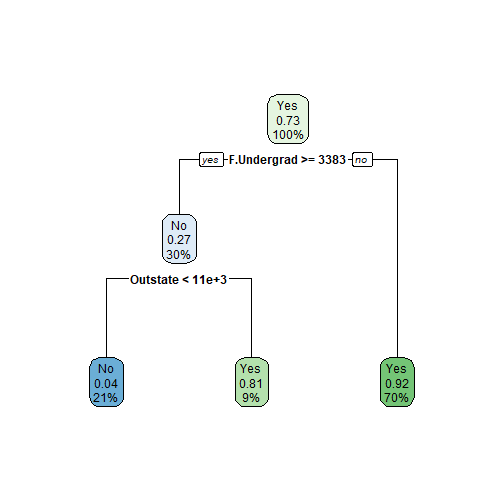
A limitação de utilizar as árvores através do train() é que o único parâmetro da árvore que pode ser alterado é o cp (complexity parameter).
modelLookup("rpart")
## model parameter label forReg forClass probModel
## 1 rpart cp Complexity Parameter TRUE TRUE TRUE
Para alterarmos o seu valor utilizamos o comando expand.grid().
controle = expand.grid(.cp = 0.0001)
modelo = caret::train(Private~., method = "rpart", data = treino, tuneGrid = controle)
modelo
## CART
##
## 545 samples
## 17 predictor
## 2 classes: 'No', 'Yes'
##
## No pre-processing
## Resampling: Bootstrapped (25 reps)
## Summary of sample sizes: 545, 545, 545, 545, 545, 545, ...
## Resampling results:
##
## Accuracy Kappa
## 0.9108212 0.7723318
##
## Tuning parameter 'cp' was held constant at a value of 0.0001
Note que com esse valor de cp a árvore fica mais profunda, pois estamos diminuindo o mínimo de ganho de ajuste que devemos ter em cada divisão.
rpart.plot(modelo$finalModel)
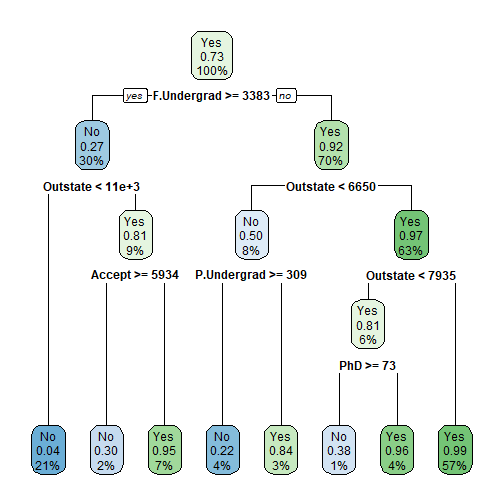
Florestas Aleatórias
As árvores de decisão possuem uma estrutura de fácil compreensão, o que faz com que ela seja bastante utilizada devido a sua boa aparência e interpretação intuitíva. Mas elas possuem uma limitação, o [sobreajuste], sendo assim, elas não são muito eficientes com novas amostras. O que fazer então?
As Florestas Aleatórias (Random Forest) se utilizam de várias árvores de decisão, combinando a simplicidade das árvores com a flexibilidade de um método sem sobreajuste, aumentando assim a precisão do preditor.
Vamos construir uma floresta aleatória usando a base de dados balloons.
balloons = readr::read_csv("balloons.csv")
balloons$Inflated = as.factor(balloons$Inflated)
str(balloons)
## tibble [20 x 5] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
## $ Color : chr [1:20] "YELLOW" "YELLOW" "YELLOW" "YELLOW" ...
## $ Size : chr [1:20] "SMALL" "SMALL" "SMALL" "SMALL" ...
## $ Act : chr [1:20] "STRETCH" "STRETCH" "STRETCH" "DIP" ...
## $ Age : chr [1:20] "ADULT" "ADULT" "CHILD" "ADULT" ...
## $ Inflated: Factor w/ 2 levels "FALSE","TRUE": 2 2 1 1 1 2 2 1 1 1 ...
## - attr(*, "spec")=
## .. cols(
## .. Color = col_character(),
## .. Size = col_character(),
## .. Act = col_character(),
## .. Age = col_character(),
## .. Inflated = col_logical()
## .. )
Com base na cor do balão, o tamanho dele, se ele é elástico ou não e se quem o está enchendo é uma criança ou um adulto, queremos predizer se o balão vai encher ou não. Portanto, nossa variável de interesse é Inflated e queremos construir um classificador.
A primeira coisa que precisamos fazer é criar uma nova amostra do mesmo tamanho da original utilizando [bootstrap].
set.seed(33)
boot1 = caret::createResample(y=balloons$Inflated, times=1, list=F)
NovaAmostra1 = balloons[boot1,]
Out_of_bag = balloons[-boot1,]
Todas as observações que não forem sorteadas vão entrar no “Out-of-Bag”. Temos 4 variáveis fora a de interesse, vamos sortear 2 variáveis para construir o primeiro nó da nossa árvore.
set.seed(413)
sample(1:4, 2)
## [1] 4 3
Vamos calcular o índice Gini para essas duas variáveis.
#calculando o indice gini para a variável tamanho
table(NovaAmostra1$Size, NovaAmostra1$Inflated)
##
## FALSE TRUE
## LARGE 9 4
## SMALL 4 3
(gini.size = (1-(7/14)^2-(7/14)^2)*(14/20) + (1-(4/6)^2-(2/6)^2)*(6/20))
## [1] 0.4833333
#calculando o indice gini para a variável idade
table(NovaAmostra1$Age, NovaAmostra1$Inflated)
##
## FALSE TRUE
## ADULT 4 7
## CHILD 9 0
(gini.age = (1-(5/14)^2-(9/14)^2)*(14/20) + (1-(6/6)^2-(0/6)^2)*(6/20))
## [1] 0.3214286
A variável idade tem um grau de impureza menor, então ela será a raiz da árvore.
Agora das variáveis que ainda não foram usadas, sorteamos mais duas para continuar a árvore.
set.seed(443)
sample(1:3, 2)
## [1] 3 2
library(dplyr)
NovaAmostra1 = filter(NovaAmostra1, Age=="ADULT")
#calculando o indice gini para a variável tamanho
table(NovaAmostra1$Size, NovaAmostra1$Inflated)
##
## FALSE TRUE
## LARGE 3 4
## SMALL 1 3
(gini.size = (1-(4/11)^2-(7/11)^2)*(11/14) + (1-(1/3)^2-(2/3)^2)*(3/14))
## [1] 0.4588745
#calculando o indice gini para a variável act
table(NovaAmostra1$Act, NovaAmostra1$Inflated)
##
## FALSE TRUE
## DIP 4 0
## STRETCH 0 7
(gini.act = (1-(5/5)^2-(0/5)^2)*(5/14) + (1-(0/9)^2-(9/9)^2)*(9/14))
## [1] 0
Como a variável act tem o menor grau de impureza, ela será o próximo nó.
Assim, temos nossa primeira árvore de decisão.
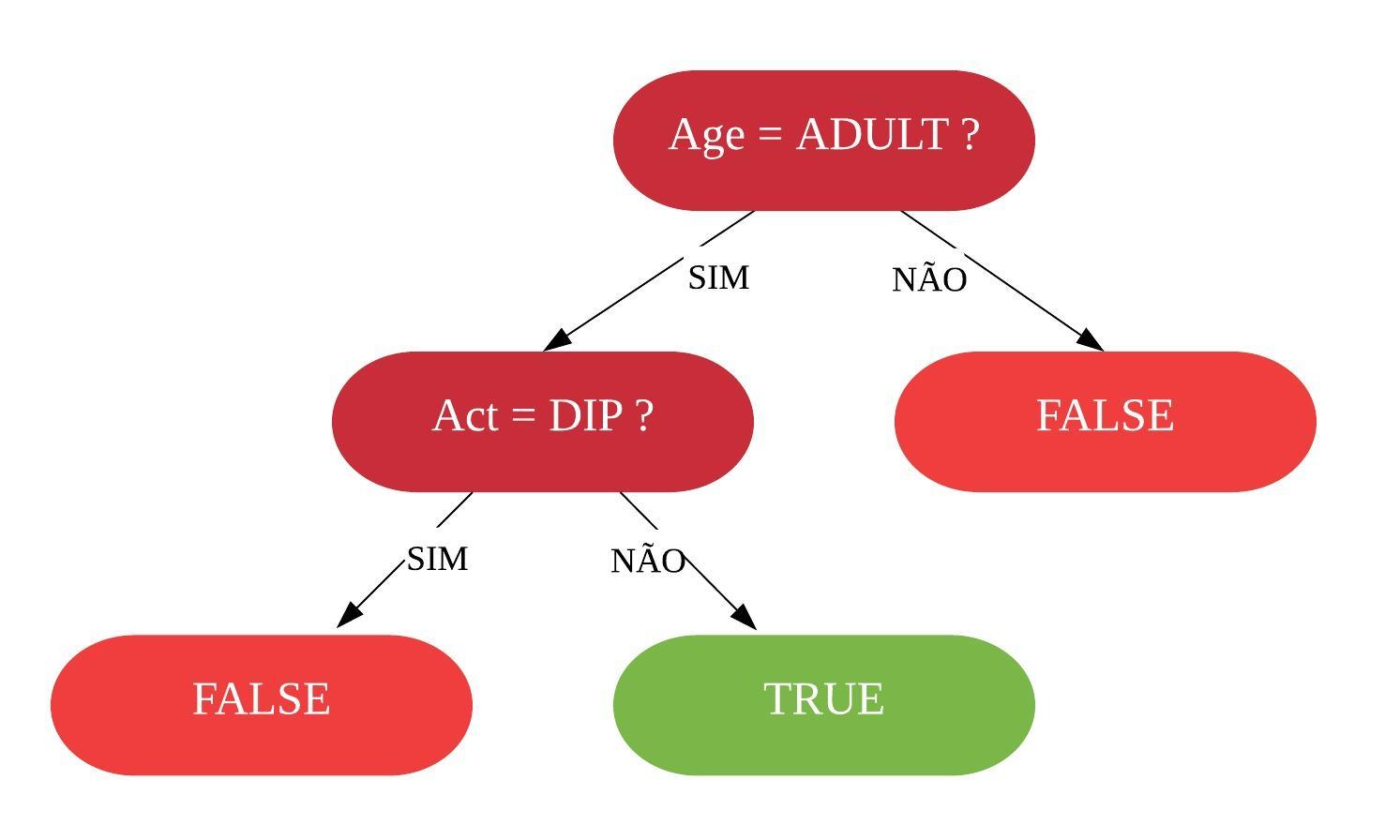
A floresta aleatória pode ser utilizada tanto em classificadores como em regressores. A diferença é que em regressores, utilizamos árvores de regressão no lugar de árvores de classificação.
Em seguida vamos construir várias árvores da mesma maneira que a anterior. Para nosso exemplo vamos construir apenas 4 árvores, mas em geral vamos fazer bem mais que isso.
Temos então nossas 4 árvores construidas.
Para classificar uma nova amostra, devemos passar ela por todas as árvores construidas e rotular a amostra pela categoria resultada mais vezes.
O método de usar bootstrap para criar novas amostras e votos para a tomada de decisão é chamado de Bagging (Bootstrap+aggregate).
As observações de cada amostra que não entraram na construção de cada árvore estão contidas Out_of_bag. Essas observações servirão para avaliar nosso preditor.
Out_of_bag = balloons[c(2,4,12,13,15,18,20,
1,2,3,5,10,
2,4,12,13,15,18,20,
2,3,11,13,14,16,19),]
knitr::kable(Out_of_bag)
| Color | Size | Act | Age | Inflated |
|---|---|---|---|---|
| YELLOW | SMALL | STRETCH | ADULT | TRUE |
| YELLOW | SMALL | DIP | ADULT | FALSE |
| PURPLE | SMALL | STRETCH | ADULT | TRUE |
| PURPLE | SMALL | STRETCH | CHILD | FALSE |
| PURPLE | SMALL | DIP | CHILD | FALSE |
| PURPLE | LARGE | STRETCH | CHILD | FALSE |
| PURPLE | LARGE | DIP | CHILD | FALSE |
| YELLOW | SMALL | STRETCH | ADULT | TRUE |
| YELLOW | SMALL | STRETCH | ADULT | TRUE |
| YELLOW | SMALL | STRETCH | CHILD | FALSE |
| YELLOW | SMALL | DIP | CHILD | FALSE |
| YELLOW | LARGE | DIP | CHILD | FALSE |
| YELLOW | SMALL | STRETCH | ADULT | TRUE |
| YELLOW | SMALL | DIP | ADULT | FALSE |
| PURPLE | SMALL | STRETCH | ADULT | TRUE |
| PURPLE | SMALL | STRETCH | CHILD | FALSE |
| PURPLE | SMALL | DIP | CHILD | FALSE |
| PURPLE | LARGE | STRETCH | CHILD | FALSE |
| PURPLE | LARGE | DIP | CHILD | FALSE |
| YELLOW | SMALL | STRETCH | ADULT | TRUE |
| YELLOW | SMALL | STRETCH | CHILD | FALSE |
| PURPLE | SMALL | STRETCH | ADULT | TRUE |
| PURPLE | SMALL | STRETCH | CHILD | FALSE |
| PURPLE | SMALL | DIP | ADULT | FALSE |
| PURPLE | LARGE | STRETCH | ADULT | TRUE |
| PURPLE | LARGE | DIP | ADULT | FALSE |
Para avaliar, é preciso passar cada uma das observações do Out_of_bag por todas as árvores e a predição será feita por votos também. Ao fazer isso, observamos uma precisão de 86%.
A proporção de amostras do Out-of-bag que foram incorretamente classificadas é chamada Out-of-bag-error
Agora que sabemos avaliar o modelo, podemos comparar florestas aleatórias construídas com 2 variáveis com as construídas com 3 e outras diferentes configurações. Tipicamente, começamos usando o quadrado do número de variáveis da base e tentamos algumas quantidades abaixo e acima.
Construindo uma floresta com o randomForest()
O pacote randomForest possui as ferramentas adequadas para a criação de uma floresta aleatória. Vamos construir uma floresta com 20 árvores utilizando a base balloons.
É importante observar se as váriaveis categóricas estão na classe de fatores.
balloons = readr::read_csv("balloons.csv")
# tratando todas as variaveis
balloons = dplyr::mutate_if(balloons, is.character, as.factor)
balloons$Inflated = as.factor(balloons$Inflated)
# construindo floresta com 20 arvores
library(randomForest)
set.seed(23)
modelo = randomForest(Inflated ~ ., data=balloons, ntree=20)
Agora, vamos avaliar a precisão do modelo.
# avaliando o modelo
modelo
##
## Call:
## randomForest(formula = Inflated ~ ., data = balloons, ntree = 20)
## Type of random forest: classification
## Number of trees: 20
## No. of variables tried at each split: 2
##
## OOB estimate of error rate: 5%
## Confusion matrix:
## FALSE TRUE class.error
## FALSE 11 1 0.08333333
## TRUE 0 8 0.00000000
Note que foram construídas 20 árvores utilizando 2 variáveis a cada vez. Essa quantidade de variáveis pode ser alterada usando o argumento
mtry=dentro do randomForest.
Podemos ver que a precisão do nosso modelo é de 19/20, ou seja, 95%. Qual seria a precisão se fosse feito apenas uma árvore?
balloons = readr::read_csv("balloons.csv")
# tratando todas as variaveis
balloons = dplyr::mutate_if(balloons, is.character, as.factor)
balloons$Inflated = as.factor(balloons$Inflated)
# separando amostras teste/treino
set.seed(45)
inTrain = caret::createDataPartition(balloons$Inflated,p=0.5,list=F)
treino = balloons[inTrain,]
teste = balloons[-inTrain,]
# treinando o modelo
controle = rpart::rpart.control(minsplit=0, cp = 0, maxdepth = 1)
set.seed(342)
modelo = rpart::rpart(Inflated~., data=treino, control = controle)
# aplicando o modelo no teste
predicao = predict(modelo,teste, type="vector")
predicao = factor(predicao, labels = c(F, T))
# avaliando o erro na amostra treino
confusionMatrix(teste$Inflated, predicao)
## Confusion Matrix and Statistics
##
## Reference
## Prediction FALSE TRUE
## FALSE 3 3
## TRUE 0 4
##
## Accuracy : 0.7
## 95% CI : (0.3475, 0.9333)
## No Information Rate : 0.7
## P-Value [Acc > NIR] : 0.6496
##
## Kappa : 0.4444
##
## Mcnemar's Test P-Value : 0.2482
##
## Sensitivity : 1.0000
## Specificity : 0.5714
## Pos Pred Value : 0.5000
## Neg Pred Value : 1.0000
## Prevalence : 0.3000
## Detection Rate : 0.3000
## Detection Prevalence : 0.6000
## Balanced Accuracy : 0.7857
##
## 'Positive' Class : FALSE
##
Note que nessa árvore, nosso modelo teve uma precisão de 80%. Bem menor do que o modelo de florestas.
Agora, observe que construimos uma floresta com 20 árvores. O que acontece com o erro do modelo conforme acrescentamos mais árvores?
Vamos avaliar o comportamento do erro conforme acrescentamos mais árvores à floresta. Para isso, utilizaremos a base de dados spam para melhor vizualização
# chamando a base
library(kernlab)
data("spam")
# construindo floresta com 20 arvores
library(randomForest)
set.seed(23)
modelo = randomForest(type ~ ., data=spam, ntree=20)
# observando o comportamento do erro em 20 árvores
erro_OOB <- data.frame(
Arvores = rep(1:nrow(modelo$err.rate), times=2),
Type = rep(c("spam", "nonspam"), each=nrow(modelo$err.rate)),
Erro = c(modelo$err.rate[,"spam"], modelo$err.rate[,"nonspam"]))
ggplot(data=erro_OOB, aes(x=Arvores, y=Erro)) +
geom_line(aes(color=Type),size=1.1) +
scale_colour_discrete(name = "Tipo",
breaks = c("nonspam", "spam"),
labels = c("Não Spam", "Spam"))
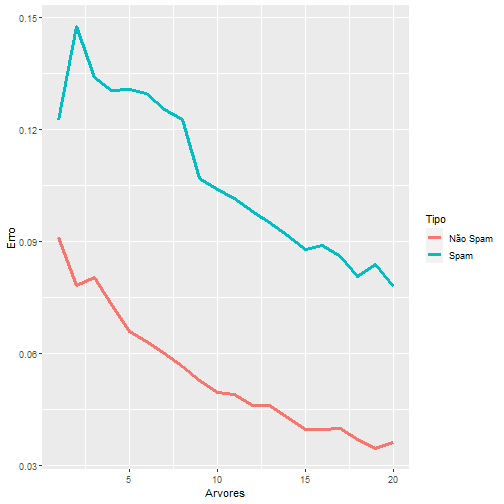
# construindo floresta com 50 arvores
set.seed(23)
modelo = randomForest(type ~ ., data=spam, ntree=50)
# observando o comportamento do erro em 50 árvores
erro_OOB <- data.frame(
Arvores=rep(1:nrow(modelo$err.rate), times=2),
Type=rep(c("spam", "nonspam"), each=nrow(modelo$err.rate)),
Erro=c(modelo$err.rate[,"spam"],
modelo$err.rate[,"nonspam"]))
ggplot(data=erro_OOB, aes(x=Arvores, y=Erro)) +
geom_line(aes(color=Type),size=1.1)+
scale_colour_discrete(name = "Tipo",
breaks = c("nonspam", "spam"),
labels = c("Não Spam", "Spam"))
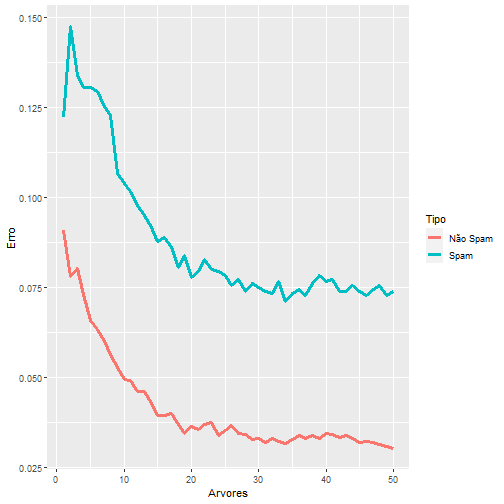
# construindo floresta com 100 arvores
set.seed(23)
modelo = randomForest(type ~ ., data=spam, ntree=100)
# observando o comportamento do erro em 100 árvores
erro_OOB <- data.frame(
Arvores=rep(1:nrow(modelo$err.rate), times=2),
Type=rep(c("spam", "nonspam"), each=nrow(modelo$err.rate)),
Erro=c(modelo$err.rate[,"spam"],
modelo$err.rate[,"nonspam"]))
ggplot(data=erro_OOB, aes(x=Arvores, y=Erro)) +
geom_line(aes(color=Type),size=1.1)+
scale_colour_discrete(name = "Tipo",
breaks = c("nonspam", "spam"),
labels = c("Não Spam", "Spam"))
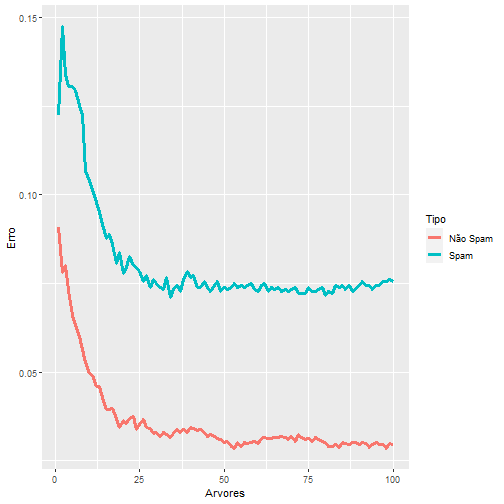
# construindo floresta com 1000 arvores
set.seed(23)
modelo = randomForest(type ~ ., data=spam, ntree=1000)
# observando o comportamento do erro em 1000 árvores
erro_OOB <- data.frame(
Arvores=rep(1:nrow(modelo$err.rate), times=2),
Type=rep(c("spam", "nonspam"), each=nrow(modelo$err.rate)),
Erro=c(modelo$err.rate[,"spam"],
modelo$err.rate[,"nonspam"]))
ggplot(data=erro_OOB, aes(x=Arvores, y=Erro)) +
geom_line(aes(color=Type),size=1.1)+
scale_colour_discrete(name = "Tipo",
breaks = c("nonspam", "spam"),
labels = c("Não Spam", "Spam"))

Repare que após uma certa quantidade de árvores, o erro se estabiliza. Sendo assim, não é necessário utilizar grandes quantidades de árvores em todos os casos. É preciso verificar até onde existe ganho.
Construindo uma floresta com o train()
Também é possivel fazer florestas aleatórias usando a função train do pacote caret. Para isso, é necessário alterar o método de reamostragem para out of bag e o método para “rf” (random forest). Vamos utilizar a base wine, construiremos um regressor para predizer a variável alcohol.
# alterando o metodo de reamostragem
controle = trainControl(method="oob")
# chamando a base
library(readr)
wine = read_csv2("winequality-red.csv")
# construindo o modelo com 50 arvores
set.seed(534)
modelo = caret::train(alcohol ∼ ., data=wine, method="rf", ntree=50, trControl=controle)
modelo
## Random Forest
##
## 1599 samples
## 11 predictor
##
## No pre-processing
## Resampling results across tuning parameters:
##
## mtry RMSE Rsquared
## 2 0.5546635 0.7289263
## 6 0.5028345 0.7772189
## 11 0.5034648 0.7766601
##
## RMSE was used to select the optimal model using the smallest value.
## The final value used for the model was mtry = 6.
Note o valor “mtry” no modelo. Ele indica a quantidade de váriaveis da base que foram utilizadas para treinar o modelo. Repare que ele calcula a RMSE e $R^2$ para diferentes quantidades de variáveis usadas e utiliza no final a quantidade que possuir menor RMSE, no caso mtry=11. Caso queira fixar o número de variáveis usadas, basta usar o seguinte comando.
tng = expand.grid(.mtry=7)
modelo = caret::train(alcohol∼., data=wine, method="rf", ntree=50, trControl=controle, tuneGrid=tng)
modelo
## Random Forest
##
## 1599 samples
## 11 predictor
##
## No pre-processing
## Resampling results:
##
## RMSE Rsquared
## 0.5127032 0.7683885
##
## Tuning parameter 'mtry' was held constant at a value of 7
AdaBoost
O método de treino AdaBoost se baseia na construção de uma floresta aleatória. Entretanto, na floresta construída por esse método as árvores possuem apenas um nó e duas folhas. Essas árvores são chamadas de tocos.
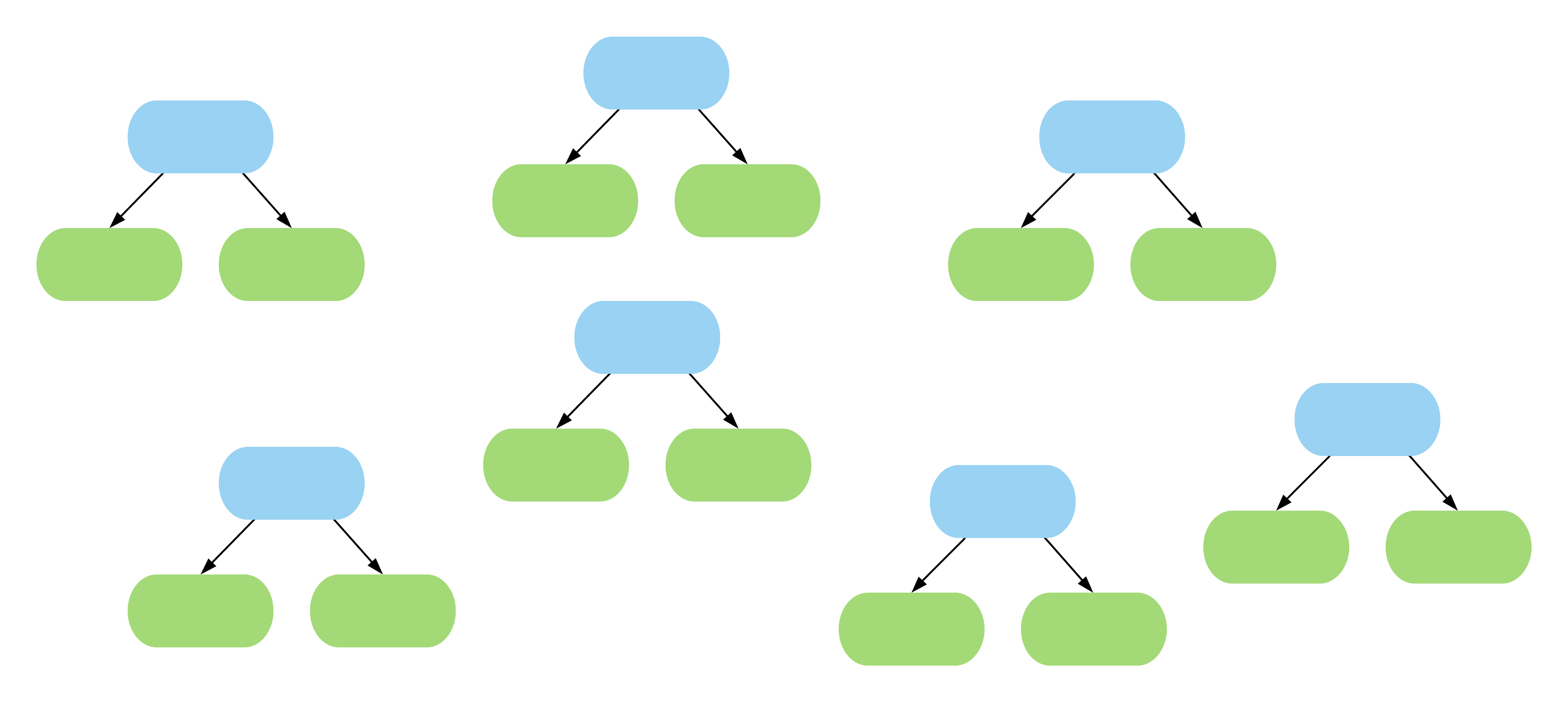
Em geral, tocos não são muito bons em fazer classificações precisas, ou seja, eles são classificadores fracos. No entanto, o método AdaBoost os combina de forma a criar um bom aprendiz. Ele faz isso utilizando diferenciais na classificação e na construção das árvores que a floresta aleatória comum não utiliza:
-
Floresta Aleatória: cada árvore de decisão tem um peso igual na classificação final das amostras. Além disso, cada árvore é construída independentemente das outras.
-
AdaBoost: alguns tocos têm mais peso na classificação final do que outros, e a ordem de construção dos tocos importam. Em outras palavras, os erros que o primeito toco comete influenciam em como o segundo toco é construído, os erros que o segundo toco comete influenciam em como o terceiro toco é construído, e assim sucessivamente.
Vamos ver os detalhes práticos de como funciona o AdaBoost utilizando o banco de dados golf. Este banco possui informações sobre condições climáticas e se o indivíduo jogou golf no dia. A ideia é tentar prever se o indivíduo vai jogar golf baseado nas outras variáveis.
golf = readRDS("Golf.rds")
golf
## # A tibble: 14 x 4
## Outlook Humidity Wind Play
## <chr> <chr> <chr> <chr>
## 1 Sunny High Weak No
## 2 Sunny High Strong No
## 3 Overcast High Weak Yes
## 4 Rain High Weak Yes
## 5 Rain Normal Weak Yes
## 6 Rain Normal Strong No
## 7 Overcast Normal Strong Yes
## 8 Sunny High Weak No
## 9 Sunny Normal Weak Yes
## 10 Rain Normal Weak Yes
## 11 Sunny Normal Strong Yes
## 12 Overcast High Strong Yes
## 13 Overcast Normal Weak Yes
## 14 Rain High Strong No
Primeiramente construímos um toco para cada uma das variáveis e calculamos seus respectivos índices Gini. Vamos começar com a variável Outlook.
library(dplyr)
golf %>% group_by(Outlook, Play) %>% summarise(N=n())
## # A tibble: 5 x 3
## # Groups: Outlook [3]
## Outlook Play N
## <chr> <chr> <int>
## 1 Overcast Yes 4
## 2 Rain No 2
## 3 Rain Yes 3
## 4 Sunny No 3
## 5 Sunny Yes 2
Então temos que “Outlook = Overcast” separa os dados da seguinte forma:
$\hbox{Gini(Outlook = Overcast)} = \frac{4}{14} \times \left[ 1- \left( \frac{4}{4} \right)^{2} - \left( \frac{0}{4} \right)^{2} \right] + \frac{10}{14} \times \left[ 1- \left( \frac{5}{10} \right)^{2} - \left( \frac{5}{10} \right)^{2} \right] = 0,357.$
Vamos agora olhar para “Outlook = Rain”:
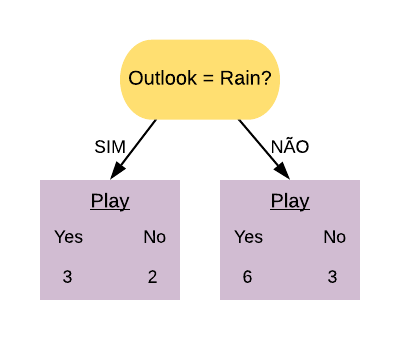
$\hbox{Gini(Outlook = Rain)} = \frac{5}{14} \times \left[ 1- \left( \frac{3}{5} \right)^{2} - \left( \frac{2}{5} \right)^{2} \right] + \frac{9}{14} \times \left[ 1- \left( \frac{6}{9} \right)^{2} - \left( \frac{3}{9} \right)^{2} \right] = 0,457.$
Por último, “Outlook = Sunny”:
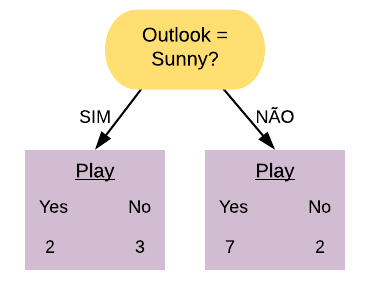
$\hbox{Gini(Outlook = Sunny)} = \frac{5}{14} \times \left[ 1- \left( \frac{2}{5} \right)^{2} - \left( \frac{3}{5} \right)^{2} \right] + \frac{9}{14} \times \left[ 1- \left( \frac{7}{9} \right)^{2} - \left( \frac{2}{9} \right)^{2} \right] = 0,394.$
Agora vamos para a variável Humidity.
golf %>% group_by(Humidity, Play) %>% summarise(N=n())
## # A tibble: 4 x 3
## # Groups: Humidity [2]
## Humidity Play N
## <chr> <chr> <int>
## 1 High No 4
## 2 High Yes 3
## 3 Normal No 1
## 4 Normal Yes 6
Temos que “Humidity = High” separa os dados da seguinte forma:

$\hbox{Gini(Humidity = High)} = \frac{7}{14} \times \left[ 1- \left( \frac{3}{7} \right)^{2} - \left( \frac{4}{7} \right)^{2} \right] + \frac{7}{14} \times \left[ 1- \left( \frac{6}{7} \right)^{2} - \left( \frac{1}{7} \right)^{2} \right] = 0,367.$
Por último, a variável Wind:
golf %>% group_by(Wind, Play) %>% summarise(N=n())
## # A tibble: 4 x 3
## # Groups: Wind [2]
## Wind Play N
## <chr> <chr> <int>
## 1 Strong No 3
## 2 Strong Yes 3
## 3 Weak No 2
## 4 Weak Yes 6
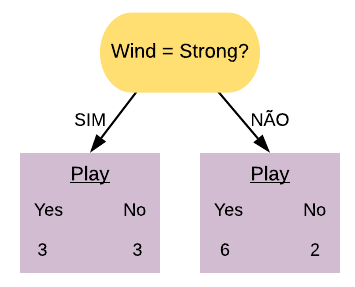
$\hbox{Gini(Wind = Strong)} = \frac{6}{14} \times \left[ 1- \left( \frac{3}{6} \right)^{2} - \left( \frac{3}{6} \right)^{2} \right] + \frac{8}{14} \times \left[ 1- \left( \frac{6}{8} \right)^{2} - \left( \frac{2}{8} \right)^{2} \right] = 0,429.$
Logo, os índices Gini calculados foram:
| Variáveis | Índice Gini |
|---|---|
| Outlook = Overcast | 0,357 |
| Outlook = Rain | 0,457 |
| Outlook = Sunny | 0,394 |
| Humidity = High | 0,367 |
| Wind = Strong | 0,429 |
Selecionamos a variável com o menor índice Gini para ser o primeiro toco da floresta. Nesse caso, o menor índice Gini é o da variável “Outlook = Overcast”.
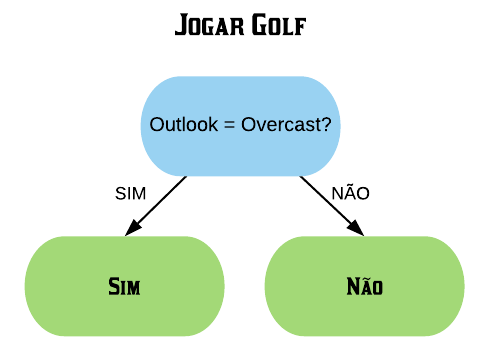
Agora precisamos calcular o peso desse toco na classificação final. Para isso, vamos calcular seu erro total.
O erro total de um toco é calculado pelo número de amostras classificadas erradas dividido pelo total de amostras.
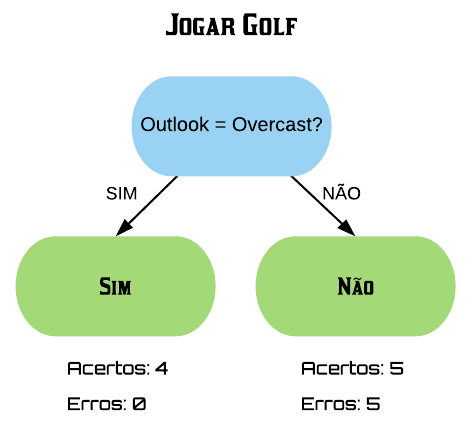
Para esse toco houve 5 amostras classificadas erradas em um total de 14. Logo,
\[\hbox{Erro Total} = \frac{5}{14}.\]Dessa forma podemos calcular o Amount of Say do toco, que será seu peso na classificação final.
\(\hbox{Amount of Say} = \frac{1}{2} \times log \left( \frac{1-\hbox{Erro Total}}{\hbox{Erro Total}} \right)\) Logo, o Amount of Say desse toco será de:
\[\hbox{Amount of Say} = \frac{1}{2} \times log \left( \frac{1-5/14}{5/14} \right) = 0,29.\]Então 0,29 é o seu peso na classificação final.
Agora vamos construir o próximo toco. Para isso damos um peso maior para as amostras que foram classificadas erroneamente no toco anterior. Essas amostras foram as seguintes:
golf %>% filter(Outlook != "Overcast" & Play != "No")
## # A tibble: 5 x 4
## Outlook Humidity Wind Play
## <chr> <chr> <chr> <chr>
## 1 Rain High Weak Yes
## 2 Rain Normal Weak Yes
## 3 Sunny Normal Weak Yes
## 4 Rain Normal Weak Yes
## 5 Sunny Normal Strong Yes
Então, para rebalancearmos os pesos das amostras classificadas de forma certa e errada, utilizamos as seguintes fórmulas:
\(\hbox{Peso Amostras Erradas} = \hbox{Erro Total} \ \times e^{\hbox{Amount of Say}}\) \(\hbox{Peso Amostras Corretas} = \hbox{Erro Total} \ \times e^{-\hbox{Amount of Say}}\)
Assim, para o segundo toco, os pesos serão:
\(\hbox{Peso Amostras Erradas} = \frac{5}{14} \ \times e^{0,29} = 0,477.\) \(\hbox{Peso Amostras Corretas} = \frac{5}{14} \ \times e^{-0,29} = 0,267.\)
Então temos os pesos para as amostras:
A soma dos pesos das amostras deve ser 1, mas isso não ocorre: note que a soma resulta em 4,788. Dessa forma, precisamos reescalar os pesos. Faremos isso dividindo cada um deles por 4,788.
Feito isso, temos uma nova tabela de pesos:
Definidos os pesos, em seguida realizamos uma reamostragem via bootstrap (uma amostragem da própria amostra, com reposição) do mesmo tamanho da base de dados original. A probabilidade de um elemento da amostra ser sorteado é o peso dele.
# Numerando os elementos da amostra:
amostra = 1:14
# Definindo as probabilidades dos elementos serem sorteados:
pesos = rep(c(0.056, 0.099, 0.056, 0.099, 0.056), times = c(3,2,3,3,3))
# Realizando o bootstrap:
set.seed(271)
sample(amostra, size = 14, replace = T, prob = pesos)
## [1] 11 7 5 5 9 10 9 11 1 11 13 12 6 3
Então temos uma nova amostra formada pelos elementos sorteados na reamostragem:
Agora, com essa nova amostra, fixamos pesos uniformes para os elementos e repetimos o processo de criação para o próximo toco. Em seguida verificamos os elementos que foram classificados de forma errada, aumentamos seus pesos no banco de dados e repetimos o processo de bootstrap, construindo, assim, o próximo toco. O processo se repete até que a floresta de tocos esteja concluída.
Finalizada a floresta, realizamos a classificação final dos elementos somando os pesos dos tocos para cada classificação e selecionando o maior deles. Por exemplo, em uma floresta com 10 árvores onde 5 delas classificam a amostra na categoria de interesse como “positivo” e 5 delas classificam essa mesma amostra como “negativo”, se a soma dos pesos das que classificaram a amostra como “positivo” for 2,7 e a das que classificaram a amostra como “negativo” for 0,84, a amostra será classificada como “positivo”.
Adaboost com o pacote adabag
Agora que já sabemos como funciona o adaboost, vamos botá-lo em prática através do pacote adabag. Vamos utilizar a base de dados spam.
Inicialmente vamos separar a amostra em treino e teste.
library(kernlab)
data(spam)
set.seed(16)
noTreino = createDataPartition(y = spam$type, p = 0.7, list = F)
treino = spam[noTreino,]
teste = spam[-noTreino,]
Antes de realizarmos o adaboost precisamos definir a profundidade máxima que as árvores da floresta terão. Faremos isso através do comando rpart.control(). Como o objetivo é construir uma floresta de tocos, as árvores terão todas profundidade 1.
library(rpart)
controle = rpart.control(maxdepth = 1)
Agora vamos aplicar o método adaboost no conjunto treino utilizando o comando boosting().
library(adabag)
set.seed(16)
modelo = boosting(formula = type~., data = treino, boos = T, mfinal = 100,
coeflearn = "Breiman", control = controle)
Os principais argumentos dessa função são:
- formula = uma fórmula especificando qual variável queremos prever em função de qual(is);
- data = base de dados onde se encontram as variáveis;
- boos = argumento do tipo logical onde, se TRUE (default), utiliza bootstrap para criar uma nova amostra treino para a próxima árvore baseado nos erros da árvore anterior;
- mfinal = número de árvores da floresta;
- coeflearn = define qual fórmula será utilizada para o Amount of Say de cada árvore. A que vimos é a fórmula de Breiman (default);
- control = opções que controlam detalhes do algoritmo rpart.
Para visualizarmos qualquer árvore da floresta utilizamos o comando rpart.plot().
library(rpart.plot)
# Visualizando a primeira árvore construída:
rpart.plot(modelo$trees[[1]])
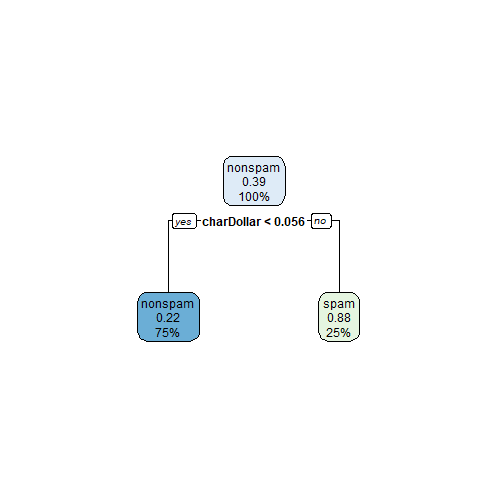
Por último, vamos aplicar o modelo na amostra teste e em seguida avaliar o modelo através da matriz de confusão.
predicao = predict(modelo, teste)
# Podemos obter a matriz de confusão com o seguinte comando:
predicao$confusion
## Observed Class
## Predicted Class nonspam spam
## nonspam 807 61
## spam 29 482
Ou utilizamos a função confusionMatrix() para, além da matriz de confusão, obtermos demais medidas avaliativas do modelo.
# Transformando em fator para utilizar a função confusionMatrix():
predicao$class = as.factor(predicao$class)
teste$type = as.factor(teste$type)
# Matriz de confusão e demais medidas avaliativas:
confusionMatrix(predicao$class, teste$type, positive = "spam")
## Confusion Matrix and Statistics
##
## Reference
## Prediction nonspam spam
## nonspam 807 61
## spam 29 482
##
## Accuracy : 0.9347
## 95% CI : (0.9204, 0.9472)
## No Information Rate : 0.6062
## P-Value [Acc > NIR] : < 0.00000000000000022
##
## Kappa : 0.8619
##
## Mcnemar's Test P-Value : 0.001084
##
## Sensitivity : 0.8877
## Specificity : 0.9653
## Pos Pred Value : 0.9432
## Neg Pred Value : 0.9297
## Prevalence : 0.3938
## Detection Rate : 0.3495
## Detection Prevalence : 0.3706
## Balanced Accuracy : 0.9265
##
## 'Positive' Class : spam
##
Repare que obtivemos uma ótima precisão e especificidade. A sensibilidade não foi tão boa quanto elas, mas talvez deva melhorar se aumentarmos o número de árvores da floresta.
Adaboost com o train
Também podemos utilizar o adaboost através da função train(). Para isso basta escolhermos a opção “AdaBoost.M1” no argumento referente ao método de treino que será utilizado. Vamos fazer isso utilizando a base de dados College.
college = readr::read_csv2("College.csv")
# Separando a amostra em treino e teste:
set.seed(100)
noTreino = caret::createDataPartition(y = college$Private, p = 0.7, list = F)
treino = college[noTreino,]
teste = college[-noTreino,]
# Para utilizar o adaboost no train primeiramente precisamos fixar os parâmetros maxdepth,
# coeflearn e mfinal:N
controle = expand.grid(maxdepth = 1, coeflearn = "Breiman", mfinal = 10)
# Treinando o modelo com o adaboost:
set.seed(100)
modelo = caret::train(Private~., method = "AdaBoost.M1", data = treino, tuneGrid = controle)
modelo
## AdaBoost.M1
##
## 545 samples
## 17 predictor
## 2 classes: 'No', 'Yes'
##
## No pre-processing
## Resampling: Bootstrapped (25 reps)
## Summary of sample sizes: 545, 545, 545, 545, 545, 545, ...
## Resampling results:
##
## Accuracy Kappa
## 0.9216357 0.7980984
##
## Tuning parameter 'mfinal' was held constant at a value of 10
## Tuning parameter 'maxdepth' was held constant at a value
## of 1
## Tuning parameter 'coeflearn' was held constant at a value of Breiman
Vamos aplicar o modelo no conjunto teste e avaliá-lo através da matriz de confusão.
predicao = predict(modelo, teste)
# Transformando em fator para depois construirmos a matriz de confusão:
teste$Private = as.factor(teste$Private)
# Construindo a matriz de confusão:
confusionMatrix(predicao, teste$Private)
## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 53 9
## Yes 10 160
##
## Accuracy : 0.9181
## 95% CI : (0.8751, 0.95)
## No Information Rate : 0.7284
## P-Value [Acc > NIR] : 0.0000000000003803
##
## Kappa : 0.792
##
## Mcnemar's Test P-Value : 1
##
## Sensitivity : 0.8413
## Specificity : 0.9467
## Pos Pred Value : 0.8548
## Neg Pred Value : 0.9412
## Prevalence : 0.2716
## Detection Rate : 0.2284
## Detection Prevalence : 0.2672
## Balanced Accuracy : 0.8940
##
## 'Positive' Class : No
##
Note que obtivemos bons resultados mesmo utilizando apenas 10 árvores. A acurácia, em particular, foi maior que 0,9, o que já é um bom indicativo de que o modelo se adequou bem aos dados.
Gradiente Boosting
em Regressão
De acordo com Jerome Friedman, o criador do Gradiente Boosting, evidências empíricas mostram que dar pequenos passos ou ir gradativamente na direção correta resulta em melhores predições na amostra teste, ou seja, menor variância.
Para entendermos como funciona o Gradiente Boosting, considere a seguinte base de dados.
## Altura Cor Sexo Peso
## 1 1.6 Azul M 88
## 2 1.6 Verde F 76
## 3 1.5 Azul F 56
## 4 1.8 Vermelho M 75
## 5 1.5 Verde M 77
## 6 1.4 Azul F 57
A primeira coisa a fazer é definir um número máximo de folhas de cada árvore. Para nosso exemplo, vamos definir 4 folhas, mas em geral, é definido uma quantidade de 8 a 32 folhas. Feito isso, tiramos uma média dos pesos dos indivíduos e essa será nossa primeira árvore, uma árvore só com a raiz.

Agora, calculamos o Pseudo-Resíduo, o erro de previsão de cada indivíduo, da forma \(Pseudo\ Resíduo = valor\ real - valor\ predito\) para cada observação. Então, por exemplo, o pseudo-resíduo da primeira observação vai ficar $88-71.5 = 16.5$ .
## Altura Cor Sexo Peso Ps..Res..1
## 1 1.6 Azul M 88 16.5
## 2 1.6 Verde F 76 4.5
## 3 1.5 Azul F 56 -15.5
## 4 1.8 Vermelho M 75 3.5
## 5 1.5 Verde M 77 5.5
## 6 1.4 Azul F 57 -14.5
O termo pseudo-resíduo é baseado em Regressão Linear, onde o resíduo é a diferença entre os valores observados e estimados. O termo “pseudo” serve para lembrar que estamos fazendo Gradiente Boosting e não Regressão Linear.
O próximo passo é, utilizando as variáveis explicativas (Altura, Cor e Sexo), construir uma árvore de decisão respeitando o máximo de folhas definido anteriormente. Mas ela deve predizer o pseudo-resíduo e não o Peso.
Note que temos mais observações do que folhas, sendo assim, podemos ter mais que um resultado em cada uma. Nesse caso, substituímos os valores pela média das folhas.
Agora somamos o resultado das duas árvores para classificar na primeira observação, por exemplo, a predição seria $71.5+16.5=88$. Acertamos exatamente o valor real. Isso é bom? Não. Já vimos como não é bom ter um modelo muito ajustado. Temos pouco viés, mas provavelmente alta variância.
O Gradiente Boosting lida com esse problema usando uma taxa de aprendizado para reescalar a contribuição da nova árvore. A taxa de aprendizado é um número entre 0 e 1 e deve ser multiplicado ao valor da segunda árvore em diante. Para esse exemplo, vamos adotar uma taxa de 0.1, assim a predição da primeira observação seria $71.5+(0.1*16.5)=73.15$. A predição não ficou tão boa, mas é um pouco melhor do que o resultado de apenas uma árvore.
Feito isso, recalculamos os valores do pseudo-resíduo.
## Altura Cor Sexo Peso Ps..Res..1 Ps..Res..2
## 1 1.6 Azul M 88 16.5 14.85
## 2 1.6 Verde F 76 4.5 4.05
## 3 1.5 Azul F 56 -15.5 -14.00
## 4 1.8 Vermelho M 75 3.5 3.05
## 5 1.5 Verde M 77 5.5 5.05
## 6 1.4 Azul F 57 -14.5 -13.00
Repare que o valor do segundo pseudo-resíduo diminuiu em módulo em relação ao primeiro, ou seja, nos aproximamos mais do valor correto do que da primeira vez.
Agora, utilizando novamente as variáveis explicativas, construímos outra árvore agora para predizer o segundo pseudo-resíduo.
Note que a estrutura da segunda árvore construída ficou semelhante a primeira. Isso não acontece sempre, mas pode acontecer.
Agora, a classificação da primeira observação ficaria $71.5+(0.116.5)+(0.114.85)=74.635$ um pouco mais perto do verdadeiro valor. Repetimos esse procedimento quantas vezes se queira ou até não ter redução significante dos valores do pseudo-resíduo. Dessa forma temos uma sequência de árvores que caminham em direção ao valor correto em passos pequenos.
É importante notar que todas as árvores devem possuir a mesma taxa de aprendizado.
Construindo um regressor com o pacote gbm
Para nosso exemplo, vamos utilizar a base de dados Wage do pacote ISLR. Para isso, vamos precisar limpar os dados removendo variáveis de variância zero.
# lendo a base de dados
library(ISLR)
data("Wage")
# removendo variaveis de variancia zero
vvz = nearZeroVar(Wage,saveMetrics = F)
vvz
## [1] 6
Wage = Wage[,-vvz]
Dividimos a base nos conjuntos de treino e teste.
set.seed(100)
noTreino = createDataPartition(Wage$wage,p=0.7,list=F)
treino = Wage[noTreino,]
teste = Wage[-noTreino,]
Agora vamos aplicar o gradiente boosting com a função gbm()
library(gbm)
set.seed(100)
modelo = gbm(wage~.,data=treino, distribution="gaussian",
n.trees =300,interaction.depth = 20)
modelo
## gbm(formula = wage ~ ., distribution = "gaussian", data = treino,
## n.trees = 300, interaction.depth = 20)
## A gradient boosted model with gaussian loss function.
## 300 iterations were performed.
## There were 9 predictors of which 9 had non-zero influence.
Os principais argumentos da função gbm() são:
- distribution: gaussian se for regressão, multinomial se for um classificação, bernoulli se for classificação 0-1.
- n.trees: número de árvores da floresta.
- interaction.depth: profundidade máxima das árvores.
Vamos aplicar o modelo na amostra teste, e avaliar o resultado.
predicao = predict(modelo, teste, n.trees=300)
# avaliando
postResample(predicao,teste$wage)
## RMSE Rsquared MAE
## 0.7297289 0.9996961 0.1742759
Note que utilizamos 300 árvores. Mas pode ser que não seja necessário essa quantidade de árvores pra alcançar esses valores de $R^2$, RMSE e MAE. Para saber a quantidade ideal de árvores, isto é, quando erro se estabiliza, podemos utilizar a função gbm.perf().
gbm.perf(modelo)
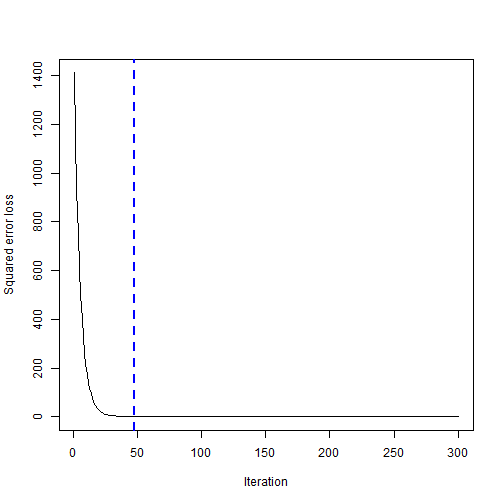
## [1] 48
## attr(,"smoother")
## Call:
## loess(formula = object$oobag.improve ~ x, enp.target = min(max(4,
## length(x)/10), 50))
##
## Number of Observations: 300
## Equivalent Number of Parameters: 24.11
## Residual Standard Error: 5.161
Sendo assim, com apenas 50 árvores teríamos chegado a um resultado razoável.
predicao2 = predict(modelo, teste, n.trees=50)
postResample(predicao2,teste$wage)
## RMSE Rsquared MAE
## 1.0759904 0.9993670 0.2823224
Podemos ver que o RMSE e o MAE aumentaram um pouco, porém o $R^{2}$ foi praticamente o mesmo. E como tivemos um custo computacional muito menor, podemos concluir que esse modelo com 50 árvores acaba sendo melhor do que o com 300.
em Classificação
Considere a seguinte base de dados
## # A tibble: 6 x 4
## `Gosta de Pipoca` Idade `Cor Favorita` `Troll 2`
## <chr> <dbl> <chr> <chr>
## 1 Sim 12 Azul Ama
## 2 Sim 87 Verde Ama
## 3 Nao 44 Azul Odeia
## 4 Sim 19 Vermelho Odeia
## 5 Nao 32 Verde Ama
## 6 Nao 14 Azul Ama
Queremos predizer se uma pessoa ama o filme Troll 2 baseado em seu gosto por pipoca, idade e cor favorita. Assim como em regressão, começamos o método de Gradiente Boosting usando uma árvore raiz que represente nossa predição inicial para cada observação. Em regressão usamos a média das observações, em classificação vamos usar o log(chances). Olhando na base de dados, podemos dizer que as chances de alguém amar Troll 2 é \(chances= \frac{Quantidade\ de\ indivíduos\ que\ amaram}{Quantidade\ de\ indivíduos\ que\ odiaram} = \frac{4}{2}\) portanto, o $log(chances)=log(\frac{4}{2}) = 0.6932$ e é isso que colocaremos na folha inicial.
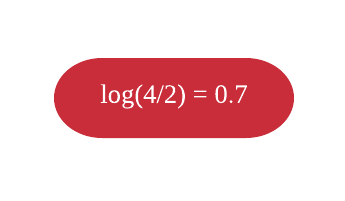
O jeito mais fácil de usar o log(chances) para classificar é convertendo em probabilidade, e fazemos isso usando a seguinte função: \(Probabilidade = \frac{e^{log(chances)}}{1+e^{log(chances)}}\) Sendo assim, A $Probabilidade\ de\ alguém\ amar\ Troll2 = \frac{e^{log(\frac{4}{2})}}{1+e^{log(\frac{4}{2})}} = \frac{2}{3}=0.6667$.
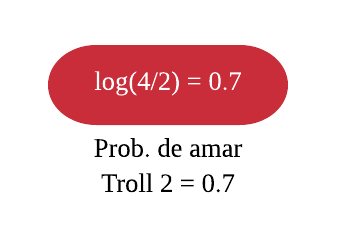
É importante notar que o log(chances) e a probabilidade só ficaram iguais por causa da aproximação.
Vamos criar o seguinte classificador:
- Probabilidade acima de 0,5: classificamos que ama Troll 2;
- Probabilidade menor ou igual a 0,5: classificamos que odeia Troll 2.
Como a probabilidade ficou maior que 0,5 classificamos todos no treino como indivíduos que amam Troll 2.
Embora 0,5 seja um limite usual para tomada de decisão baseada em probabilidade, poderiamos tranquilamente usar um valor diferente.
Mas a classificação não ficou muito boa já que 2 indivíduos foram classificados erroneamente. Podemos mensurar quão ruim foi a predição calculando o $pseudo\ resíduo = observado - predito$. Para essa conta, perceba que se um indivíduo ama Troll 2, então a probabilidade dele amar Troll 2 é 1. Semelhantemente, se ele odeia, a probabilidade dele amar é 0. Assim, calculamos os pseudo-resíduos.
## # A tibble: 6 x 5
## `Gosta de Pipoca` Idade `Cor Favorita` `Troll 2` `Ps. Res. 1`
## <chr> <dbl> <chr> <chr> <dbl>
## 1 Sim 12 Azul Ama 0.3
## 2 Sim 87 Verde Ama 0.3
## 3 Nao 44 Azul Odeia -0.7
## 4 Sim 19 Vermelho Odeia -0.7
## 5 Nao 32 Verde Ama 0.3
## 6 Nao 14 Azul Ama 0.3
Agora construímos uma árvore utilizando as variáveis explicativas para predizer o pseudo-resíduo. Assim como o Gradiente Boosting para regressão, temos que definir um número máximo de folhas em cada árvore. Aqui vamos limitar a 3 folhas, mas na prática geralmente é um número entre 8 e 32.
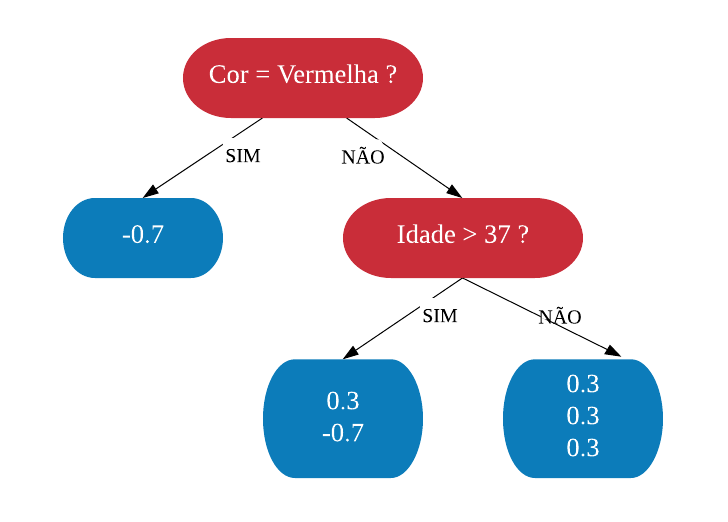
Em regressão, os valores das folhas representavam os resíduos. Mas em classificação isso é mais complexo. Isso porque a predição está em log(chances) e as folhas são provenientes de probabilidade. Portanto não podemos apenas somá-las para uma nova predição sem alguma transformação. A transformação mais comum por folha é \(\frac{\sum resíduos}{\sum[prob.\ anterior * (1-prob.\ anterior)]}\)
Assim, da esquerda pra direita, para primeira folha temos \(\frac{\sum resíduos}{\sum[prob.\ anterior * (1-prob.\ anterior)]}=\frac{-0.7}{0.7*(1-0.7)}=-3.3333,\) para a segunda \(\frac{\sum resíduos}{\sum[prob.\ anterior * (1-prob.\ anterior)]}=\frac{0.3+(-0.7)}{(0.7*(1-0.7))+(0.7*(1-0.7))}=-0.9524\) e para a última \(\frac{\sum resíduos}{\sum[prob.\ anterior * (1-prob.\ anterior)]}=\) \(\frac{0.3+0.3+0.3}{(0.7*(1-0.7))+(0.7*(1-0.7))+(0.7*(1-0.7))}=\frac{3*0.3}{3*(0.7*(1-0.7))}=1.4286\)
Por enquanto, a probabilidade anterior é a mesma para todos, mas a partir da próxima árvore isso muda.
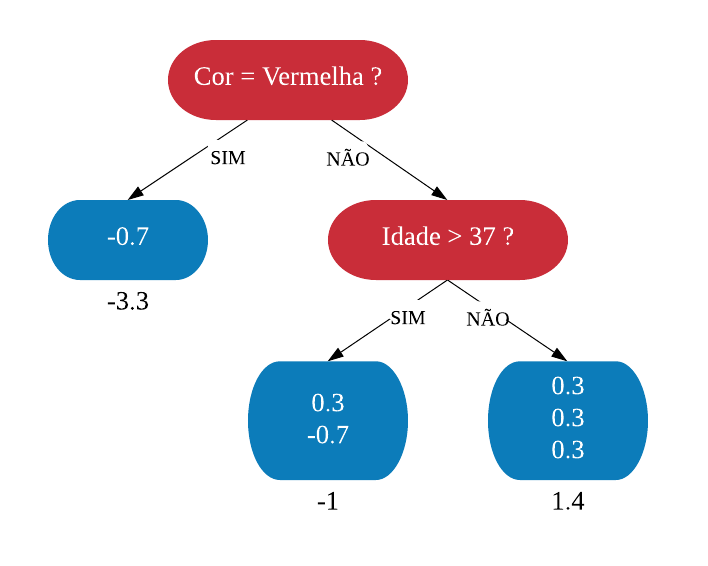
Agora que todas as folhas foram alteradas, podemos somar os resultados escalados pela taxa de aprendizado. Nesse exemplo, vamos usar uma taxa alta, 0.8. Mas geralmente se usa 0.1. E então calculamos o novo $log(chances)=log(chances)\ anterior + taxa\ de\ aprendizado * log(chances)\ obtido\ na\ árvore$. Para primeira observação, por exemplo, fica $log(chances)=0.7+(0.8*1.4)=1.82$ e então convertemos em probabilidade $\frac{e^{1.82}}{1+e^{1.82}} = 0.8606$. Então, note que fizemos progresso, já que o indivíduo em questão ama Troll 2. Antes ele foi classificado corretamente mas com probabilidade 0.7, agora ele foi classificado corretamente mas com probabilidade 0.9.
## # A tibble: 6 x 5
## `Gosta de Pipoca` Idade `Cor Favorita` `Troll 2` `Prob. Predita`
## <chr> <dbl> <chr> <chr> <dbl>
## 1 Sim 12 Azul Ama 0.9
## 2 Sim 87 Verde Ama 0.5
## 3 Nao 44 Azul Odeia 0.5
## 4 Sim 19 Vermelho Odeia 0.1
## 5 Nao 32 Verde Ama 0.9
## 6 Nao 14 Azul Ama 0.9
Pode ser que a previsão fique pior, como no caso do segundo indivíduo. E essa é a razão de construírmos várias árvores e não só uma.
Calculamos os novos pseudo-resíduos que agora serão diferentes para cada observação.
## # A tibble: 6 x 5
## `Gosta de Pipoca` Idade `Cor Favorita` `Troll 2` `Ps. Res. 2`
## <chr> <dbl> <chr> <chr> <dbl>
## 1 Sim 12 Azul Ama 0.1
## 2 Sim 87 Verde Ama 0.5
## 3 Nao 44 Azul Odeia -0.5
## 4 Sim 19 Vermelho Odeia -0.1
## 5 Nao 32 Verde Ama 0.1
## 6 Nao 14 Azul Ama 0.1
Construímos uma segunda árvore agora para prever os novos pseudo-resíduos e fazemos a transformação para log(chances) para cada folha.
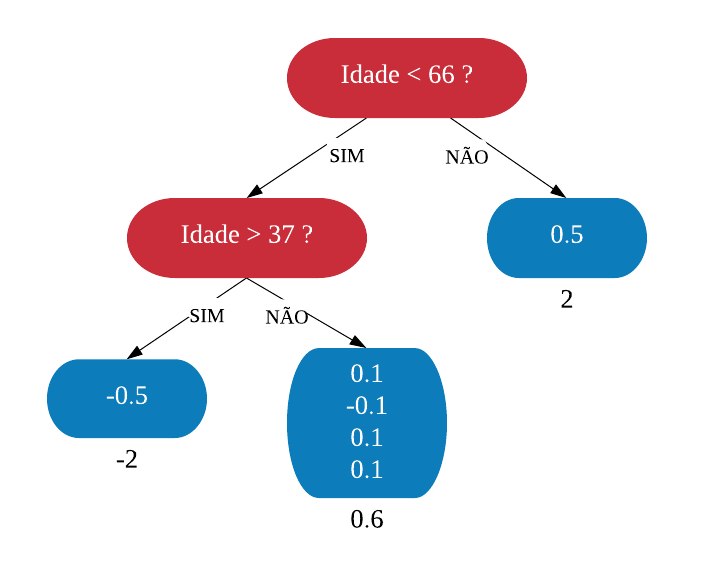
Combinamos com as árvores anteriores para obter um valor de saída e transformamos em Probabilidade para classificar. Por exemplo, a primeira observação ficaria $log(chances)=0.7+(0.81.4)+(0.80.6)=2.3$ e então convertemos em probabilidade $\frac{e^{1.82}}{1+e^{1.82}} = 0.9089$. Dessa forma, continuamos construíndo quantas árvores forem necessárias.
Construindo um classificador com o pacote gbm
O gradiente boosting para classificação no R é semelhante ao para regressão, atentando para o argumento distribution, que deve ser igual a “bernoulli” se a variável de interesse tiver apenas duas respostas possíveis (como no caso da bse Troll 2) ou “multinomial” se a variável tiver mais de duas respostas possíveis. Por exemplo, considere a base Vehicle do pacote mlbench. Nela, estamos interessados em classificar a variável Class, que pode ser bus, opel, saab ou van.
# lendo a base
library(mlbench)
data(Vehicle)
# dividindo em treino e teste
library(caret)
set.seed(100)
noTreino = createDataPartition(Vehicle$Class,p=0.7,list=F)
treino = Vehicle[noTreino,]
teste = Vehicle[-noTreino,]
# treinando o modelo
library(gbm)
set.seed(100)
modelo = gbm(Class~.,data=treino,distribution="multinomial",
n.trees = 100,interaction.depth = 8)
Quando aplicamos o predict(), o que recebemos de retorno são um conjunto de probabilidades (ou o log(chances)), e não a classificação final. Cabe ao pesquisador definir a regra de classificação final.
predicao = predict(modelo, teste, n.trees = 100, type = 'response')
O argumento ´type´ retorna por default o log(chances), se definimos como “response” ele retorna a probabilidade.
# Criando a regra de classificacao
k = dim(teste)[1]
classe = c()
for (i in 1:k){
classe[i] = names(which.max(predicao[i,1:4,1]))
}
head(classe)
## [1] "van" "van" "opel" "van" "bus" "saab"
# verificando quantidade de arvores necessarias
gbm.perf(modelo)
## [1] 16
## attr(,"smoother")
## Call:
## loess(formula = object$oobag.improve ~ x, enp.target = min(max(4,
## length(x)/10), 50))
##
## Number of Observations: 100
## Equivalent Number of Parameters: 8.32
## Residual Standard Error: 0.0121
# avaliando o modelo
confusionMatrix(data=as.factor(classe), reference=as.factor(teste$Class))
## Confusion Matrix and Statistics
##
## Reference
## Prediction bus opel saab van
## bus 62 2 0 1
## opel 0 39 23 1
## saab 3 20 39 0
## van 0 2 3 57
##
## Overall Statistics
##
## Accuracy : 0.7817
## 95% CI : (0.7256, 0.8311)
## No Information Rate : 0.2579
## P-Value [Acc > NIR] : <0.0000000000000002
##
## Kappa : 0.709
##
## Mcnemar's Test P-Value : 0.1453
##
## Statistics by Class:
##
## Class: bus Class: opel Class: saab Class: van
## Sensitivity 0.9538 0.6190 0.6000 0.9661
## Specificity 0.9840 0.8730 0.8770 0.9741
## Pos Pred Value 0.9538 0.6190 0.6290 0.9194
## Neg Pred Value 0.9840 0.8730 0.8632 0.9895
## Prevalence 0.2579 0.2500 0.2579 0.2341
## Detection Rate 0.2460 0.1548 0.1548 0.2262
## Detection Prevalence 0.2579 0.2500 0.2460 0.2460
## Balanced Accuracy 0.9689 0.7460 0.7385 0.9701
Note que o modelo obteve uma precisão razoável de 75,79%.
XGBoost
O XGBoost é a abreviação de Extreme Gradient Boost. Ele foi desenvolvido para suportar um grande volume de dados de forma eficiente. Geralmente é 10 vezes mais rápido que o Gradiente Boosting.
Em Regressão
Apesar do XGBoost ser usado para lidar com bases grandes, vamos usar uma base de dados bem pequena só para entendermos melhor como ele funciona. Para isso considere a seguinte situação: queremos predizer o peso de um indivíduo em função de sua altura.
# lendo e vizualizando a base
library(readr)
peso = read_csv("peso-altura.csv")
library(ggplot2)
ggplot(peso, aes(x=Altura, y=Peso)) + geom_point(lwd=5, colour = "deeppink3") +
theme_minimal() + ylim(c(50,90)) + xlim(c(1.3,1.9))
O primeiro passo é fazer uma predição inicial, que pode ser qualquer uma. O default é usar 0,5, mas como estamos falando de peso, vamos utilizar a predição inicial “Peso = 70”.

Agora precisamos calcular os resíduos (diferença entre o valor real e o valor predito) que vão nos mostrar quão boa é essa predição.
library(dplyr)
(peso = peso %>% mutate( residuos = Peso-70 ))
## # A tibble: 5 x 3
## Altura Peso residuos
## <dbl> <dbl> <dbl>
## 1 1.7 88 18
## 2 1.6 76 6
## 3 1.5 56 -14
## 4 1.8 75 5
## 5 1.4 60 -10
Assim como no Gradiente Boosting, o próximo passo é construir uma árvore para predizer os resíduos. Mas o XGBoost utiliza uma árvore de regressão diferente que vamos chamar de árvore XGB. Existem muitas formas de construir uma árvore XGB. Vamos aprender a mais comum. A árvore XGB inicia com uma folha que leva todos os resíduos.
Em seguida, calculamos um índice de qualidade ou Índice de similaridade \(Índice\ Similaridade\ = \frac{(soma\ dos\ resíduos)^2}{número\ de\ resíduos + \lambda}\) Onde $\lambda$ (lambda) é um parâmetro de regularização, o que significa que tem o objetivo de reduzir a sensibilidade das observações individuais, ou seja, reduzir o sobreajuste. Por enquanto, vamos considerar $\lambda = 0$ porque esse é o valor default. Sendo assim, o Índice de similaridade da raiz é $\frac{(18+6-14+5-10)^2}{5+0}=\frac{5^2}{5}=5$

Agora vamos ver se conseguimos melhorar esse índice dividindo os resíduos, ou seja, criando uma ramificação. Vamos começar dividindo a variável Altura na média entre os dois menores valores, que são $1.4$ e $1.5$, e calculando o Indice para as novas folhas.
Observe que nas folhas não estarão as alturas e sim os resíduos correspondentes a altura especificada.
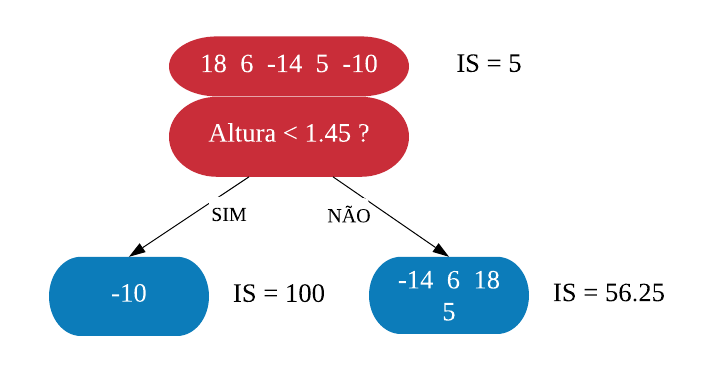
Agora, precisamos calcular o ganho dessa ramificação para ver o quanto ela foi efetiva. O ganho é calculado da seguinte forma: \(ganho = IS_{folha\ da\ esquerda} + IS_{folha\ da\ direita} - IS_{raiz}\) Assim, o ganho da ramificação ‘Altura<1.45’ é $100 + 56.25 - 5 = 151.25$. Vamos fazer esse calculo em todas as ramificações possiveis, Isto é, se temos 5 observações com diferentes alturas, vamos ter 4 ramificações possiveis: ‘Altura<1.45’, ‘Altura<1.55’, ‘Altura<1.65’ e ‘Altura<1.75’.
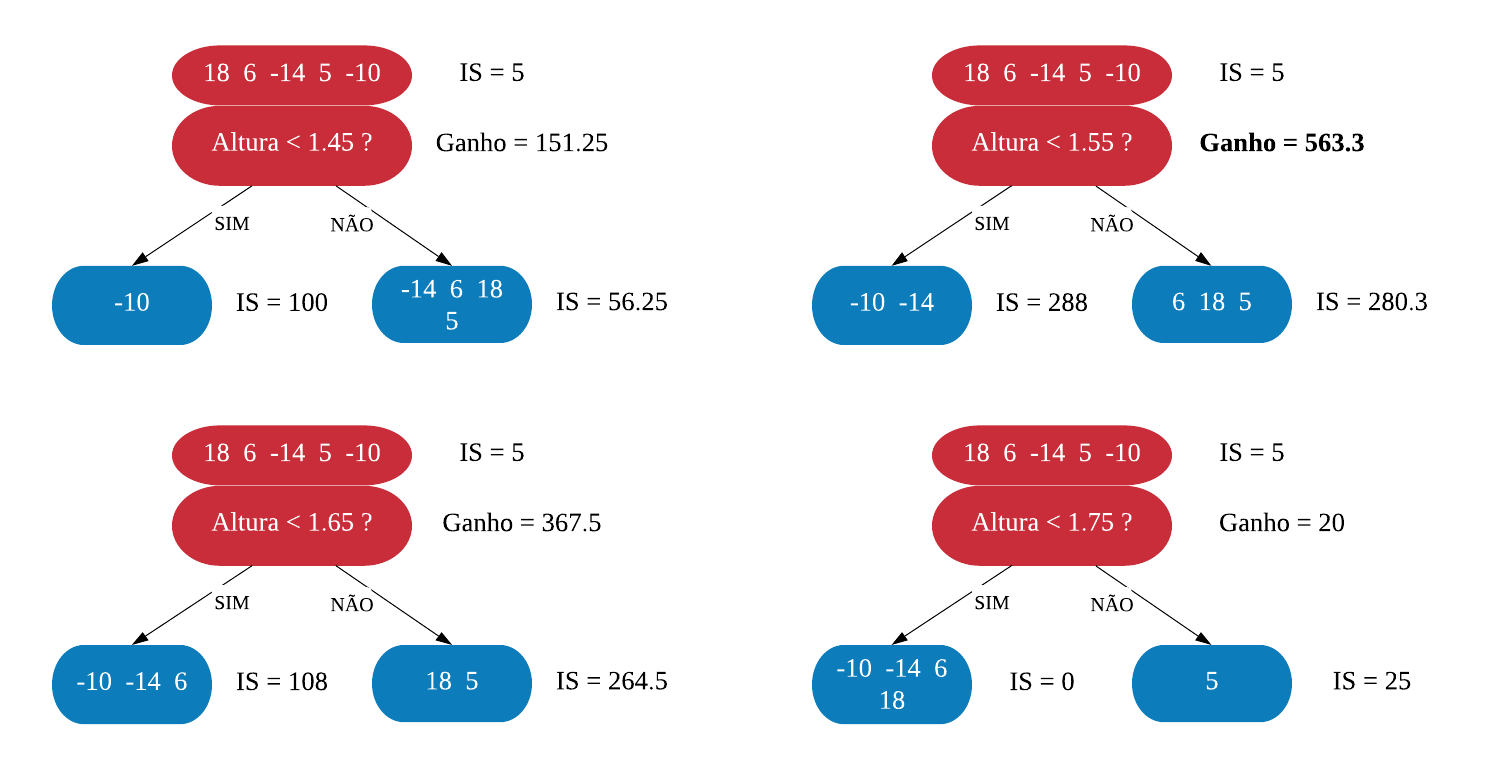
Podemos ver que o ganho de usar a ramificação ‘Altura<1.55’ é maior, portanto é essa que vamos usar. Agora vamos ramificar as folhas da mesma maneira e escolher as que tiverem melhor ganho.
Nesse exemplo, vamos limitar a profundidade da árvore XGB em 2. Mas o default é permitir até 6 níveis de profundidade.
Nossa árvore XGB final ficou:
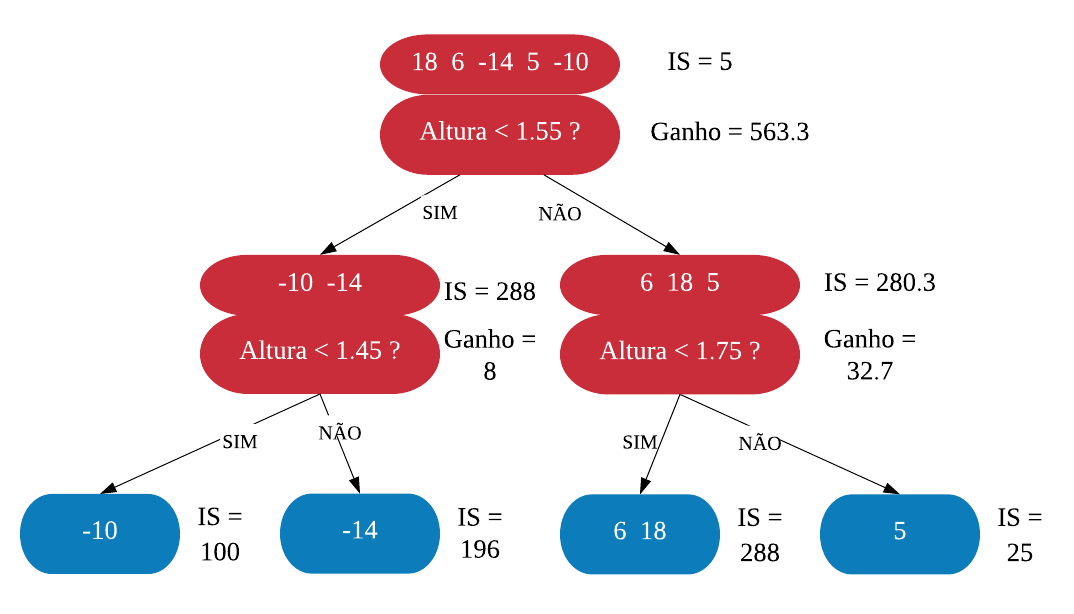
Agora, vamos podar nossa árvore. Fazemos isso porque pode ser que algum nó tenha o ganho muito baixo e por isso não vale a pena estar na árvore. Para decidir se vamos tirar algum nó e, se sim, qual, vamos escolher um valor que será chamado de $\gamma$ (gamma). Em seguida, calculamos a diferença entre o ganho associado ao nó e $\gamma$, se essa diferença for negativa, então removemos o nó.
$\gamma$ especifica o ganho mínimo necessario para fazer uma divisão. Seu default é 0. Quanto maior, mais conservador é o modelo.
Mesmo quando $\gamma = 0$ isso não previne podas.
Vamos escolher $\gamma = 10$. Começando sempre dos nós mais profundos para a raiz, vamos avaliar a diferença entre o ganho e $\gamma$. No nó mais à direita temos que o ganho é 32,7, portanto a diferença é $32,7-10=22,7$. Como o resultado é positivo, o nó permanece. No nó à esquerda, a diferença fica $8-10=-2$, e, como o resultado é negativo, retiramos esse nó. Assim, estamos dizendo que o ganho do nó à esquerda não é bom o suficiente pra justificar essa ramificação. Como o nó à direita permaneceu na árvore, não faz sentido calcular essa diferença para o nó raiz.
Mesmo se o valor da diferença der negativo nos nós de cima, se não removermos o de baixo, o de cima não é removido.
Com isso, nossa árvore XGB ficou:
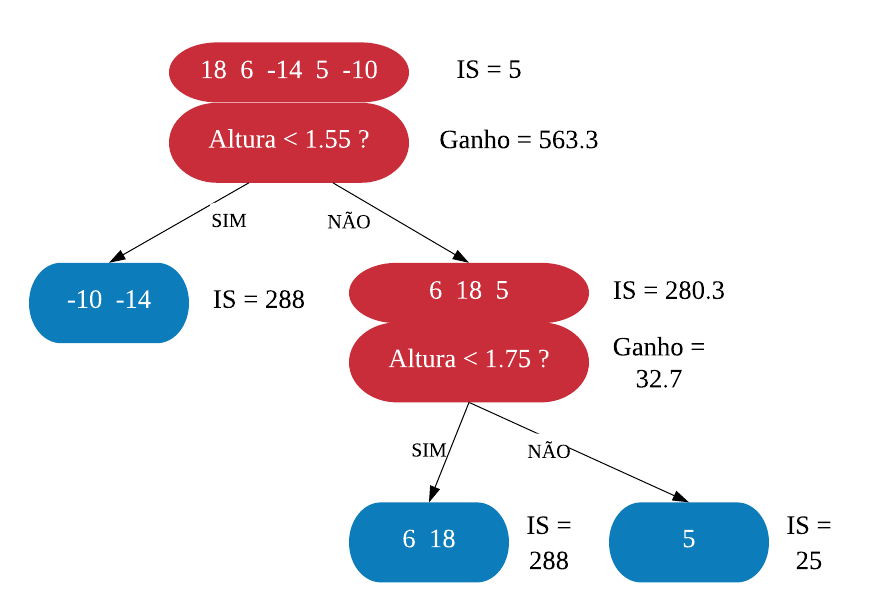
Note que se tivéssemos escolhido um $\gamma$ muito alto, por exemplo $\gamma = 570$, toda árvore seria podada. É preciso cuidado.
Agora vamos voltar ao inicio e reconstruir a árvore agora usando $\lambda = 1$ (lembra do $\lambda$? aquele da fórmula do índicador de similaridade :) ). Para facilitar a vizualização, vamos omitir os cálculos. A nova árvore XGB ficou:
Podemos notar que quando $\lambda > 0$, o índice de similaridade é menor. O que significa que se mantivermos o mesmo $\gamma$, a poda será mais extrema. Por outro lado, deixar $\lambda > 0$ ajuda a previnir sobreajustes.
Agora que temos árvore final, vamos calcular os valores de saída das folhas. \(valores\ de\ saida = \frac{soma\ dos\ residuos}{número\ de\ resíduos + \lambda}\) Repare que essa fórmula é bem parecida com a do índice de similaridade, mas a soma dos resíduos não está ao quadrado.
Repare que, como $\lambda = 0$ o valor de saida é uma média aritmética simples entre os resíduos. Mas note que se $\lambda > 0$ e a folha tiver apenas uma observação, isso reduzira a sensibilidade dessa observação individual evitando sobreajuste.
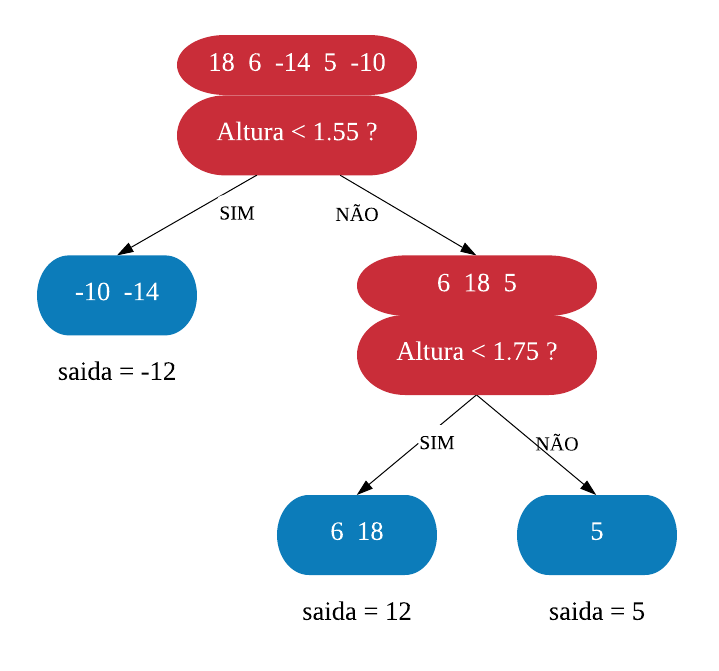
Assim a primeira árvore está completa e, como em Gradient Boosting, fazemos novas predições começando com a predição inicial e somando com o resultado da árvore XGB escalada pela taxa de aprendizado.
O XGBoost chama a taxa de aprendizado de $\varepsilon$ (eta) e seu valor default é 0.3, que é o que vamos usar.
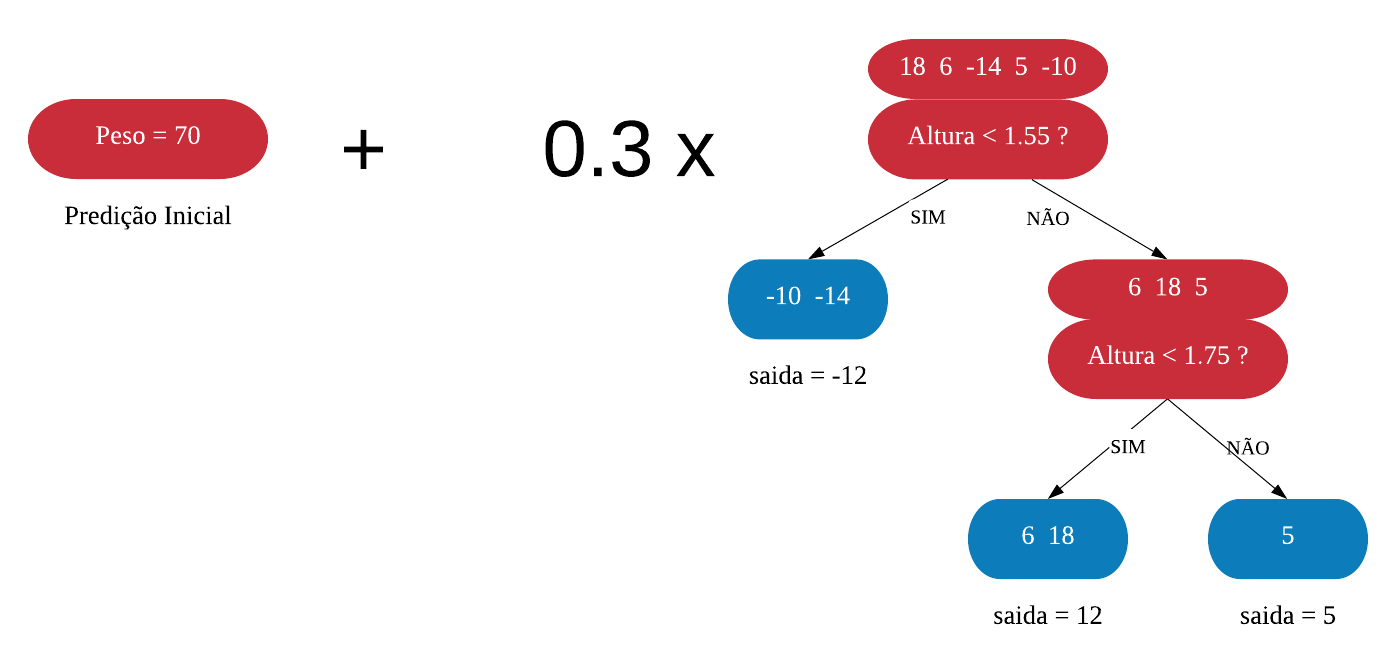
Por exemplo, se a gente pegasse a primeira observação (indivíduo com altura=1.7), seu peso predito seria $predicao\ inicial + \varepsilonvalor\ de\ saida\ da \ árvore\ XGB = 70+0.312=73.6$ que é mais perto do seu peso real (que era 88) do que a predição anterior (70). Assim, com as novas predições, os novos resíduos ficaram:
nova_pred = c(73.6, 73.6, 66.4, 71.5, 66.4)
(peso = peso %>% mutate( residuos2 = Peso - nova_pred ))
## # A tibble: 5 x 4
## Altura Peso residuos residuos2
## <dbl> <dbl> <dbl> <dbl>
## 1 1.7 88 18 14.4
## 2 1.6 76 6 2.4
## 3 1.5 56 -14 -10.4
## 4 1.8 75 5 3.5
## 5 1.4 60 -10 -6.4
Perceba que o novo resíduo é melhor que o anterior (seu valor absoluto é mais próximo de 0). Ou seja, estamos dando pequenos passos na direção correta.
Agora construímos outra árvore XGB da mesma forma, mas para predizer os novos resíduos, Dessa forma obteremos previsões com resíduos menores. E continuamos construíndo árvores XGB até que os resíduos sejam bem pequenos ou até atingir o número de árvores desejado.
Construindo um regressor com o pacote xgboost
Vamos usar a base de dados winequality-red. O objetivo dessa base é prever a qualidade do vinho baseado em suas outras variáveis. Mas nós vamos tentar prever o nível alcoólico do vinho.
library(readr)
wine = read_csv2("winequality-red.csv")
str(wine)
## tibble [1,599 x 12] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
## $ fixed acidity : num [1:1599] 7.4 7.8 7.8 11.2 7.4 7.4 7.9 7.3 7.8 7.5 ...
## $ volatile acidity : num [1:1599] 0.7 0.88 0.76 0.28 0.7 0.66 0.6 0.65 0.58 0.5 ...
## $ citric acid : num [1:1599] 0 0 0.04 0.56 0 0 0.06 0 0.02 0.36 ...
## $ residual sugar : num [1:1599] 1.9 2.6 2.3 1.9 1.9 1.8 1.6 1.2 2 6.1 ...
## $ chlorides : num [1:1599] 0.076 0.098 0.092 0.075 0.076 0.075 0.069 0.065 0.073 0.071 ...
## $ free sulfur dioxide : num [1:1599] 11 25 15 17 11 13 15 15 9 17 ...
## $ total sulfur dioxide: num [1:1599] 34 67 54 60 34 40 59 21 18 102 ...
## $ density : num [1:1599] 0.998 0.997 0.997 0.998 0.998 ...
## $ pH : num [1:1599] 3.51 3.2 3.26 3.16 3.51 3.51 3.3 3.39 3.36 3.35 ...
## $ sulphates : num [1:1599] 0.56 0.68 0.65 0.58 0.56 0.56 0.46 0.47 0.57 0.8 ...
## $ alcohol : num [1:1599] 9.4 9.8 9.8 9.8 9.4 9.4 9.4 10 9.5 10.5 ...
## $ quality : num [1:1599] 5 5 5 6 5 5 5 7 7 5 ...
## - attr(*, "spec")=
## .. cols(
## .. `fixed acidity` = col_double(),
## .. `volatile acidity` = col_double(),
## .. `citric acid` = col_double(),
## .. `residual sugar` = col_double(),
## .. chlorides = col_double(),
## .. `free sulfur dioxide` = col_double(),
## .. `total sulfur dioxide` = col_double(),
## .. density = col_double(),
## .. pH = col_double(),
## .. sulphates = col_double(),
## .. alcohol = col_double(),
## .. quality = col_double()
## .. )
Como sempre, vamos dividir a base em amostra de treino e amostra de teste.
library(caret)
set.seed(100)
noTreino = createDataPartition(wine$alcohol, p = 0.7, list = F)
# vendo a classe da base de dados
class(wine)
## [1] "spec_tbl_df" "tbl_df" "tbl" "data.frame"
O pacote xgboost só le matrizes. Então teremos que transformar a base numa matriz. Além disso, teremos que separar a váriavel de interesse das variáveis explicativas.
# Transformando a base em matriz
wine = as.matrix(wine)
class(wine)
## [1] "matrix" "array"
# separando amostra treino e teste
treino = wine[noTreino,-11] # a variável 'alcohol' é a 11ª coluna
treino_label = wine[noTreino, 11]
teste = wine[-noTreino,-11]
teste_label = wine[-noTreino, 11]
Agora, podemos usar a função xgboost para criar nosso modelo.
library(xgboost)
set.seed(100)
modelo = xgboost(data = treino, label = treino_label,
gamma=0, eta=0.3,
nrounds = 100, objective = "reg:squarederror",
verbose = 0)
Os principais argumentos da função xgboost são:
- data: recebe a amostra treino apenas com as variáveis explicativas;
- label: recebe a variável de interesse;
- gamma: ganho mínimo necessário para fazer uma divisão;
- eta: taxa de aprendizado;
- nrounds: representa o número de iterações;
- objective: é o tipo de predição que será feita. Para mais informações, veja nesse site.;
- verbose: se for 1, que é o default, o xgboost vai imprimir informações de desempenho a cada iteração. Se for 0, não vai imprimir nada.
Para fazer a predição usamos o conhecido predict(). Em seguida, vamos avaliar os resultados do modelo utilizando a função defaultSummary() do pacote caret. Essa função nos retorna os valores do RMSE, $R^{2}$ e MAE do modelo. Para isso devemos passar como argumento um dataframe onde a primeira coluna são os valores observados dos rótulos do conjunto teste e a segunda coluna são os valores preditos pelo modelo.
predicao = predict(modelo,teste)
# Calculando o RMSE do modelo:
caret::defaultSummary(data.frame(obs = teste_label, pred = predicao))
## RMSE Rsquared MAE
## 0.5394468 0.7435102 0.3548454
Considerando a escala em que os dados se encontram, o valor do RMSE foi um pouco grande. Em contrapartida podemos considerar os valores do MAE e do $R^{2}$ como sendo razoáveis para o modelo. Em particular, um $R^{2}$ de aproximadamente 0,7881 nos indica que o modelo tem um poder de explicação de 78,81%.
Em Classificação
Para entendermos como o XGBoost funciona para problemas de classificação, vamos utilizar a base de dados a seguir. O objetivo é prever se a universidade é pública ou privada baseado nos pedidos para ingresso.
OBS: Assim como comentado anteriormente em regressão, o XGBoost foi projetado para bases de dados grandes, mas para fins didáticos iremos utilizar uma base bem pequena.
library(readxl)
college = read_excel("SmallCollege.xlsx")
college
## # A tibble: 4 x 2
## Private Apps
## <chr> <dbl>
## 1 No 2119
## 2 Yes 1660
## 3 Yes 2694
## 4 No 2785
library(ggplot2)
library(dplyr)
# Construindo um gráfico para os pedidos para ingresso x tipo da universidade:
college %>% ggplot(aes(x = Apps, y = Private)) + geom_point(lwd = 5, aes(colour = Private)) +
guides(col = F) + theme_minimal() + ggtitle("Pedidos para Ingresso x Tipo da Universidade") +
xlab("Pedidos para Ingresso") + ylab("Universidade Privada")
O primeiro passo é fazer uma predição inicial. Essa predição pode ser qualquer valor, como por exemplo a probabilidade de observar universidades públicas no conjunto de dados. Por default, essa predição é de 0,5.

Podemos ilustrar essa predição inicial adicionando uma linha horizontal no gráfico que representa as probabilidades de uma universidade ser pública pelo que observamos no conjunto de dados.
# Vamos adicionar a coluna "Probabilidade" na base de dados que conterá a probabilidade da
# universidade ser pública:
college$Probabilidade = ifelse(college$Private == "Yes", 0, 1)
# Gráfico dos pedidos para ingresso x probabilidade da universidade ser pública baseado no
# conjunto de dados:
college %>% ggplot(aes(x = Apps, y = Probabilidade)) +
geom_point(lwd = 5, aes(colour = Private)) + theme_minimal() +
ylab("Probabilidade da Universidade ser Pública") +
geom_hline(yintercept = 0.5, type = 2) +
ggtitle("Pedidos para Ingresso x Probabilidade da Universidade ser Pública") +
xlab("Pedidos para Ingresso") + guides(col = F)
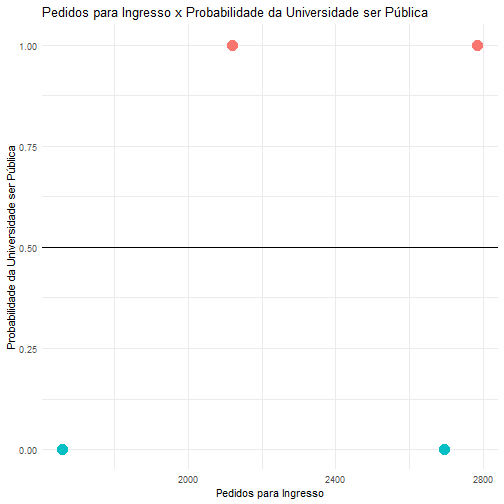
Feita a predição inicial, agora vamos calcular os resíduos e verificar quão boa é essa predição.
college$Residuos = college$Probabilidade-0.5
college
## # A tibble: 4 x 4
## Private Apps Probabilidade Residuos
## <chr> <dbl> <dbl> <dbl>
## 1 No 2119 1 0.5
## 2 Yes 1660 0 -0.5
## 3 Yes 2694 0 -0.5
## 4 No 2785 1 0.5
O próximo passo é construir uma árvore para predizer os resíduos. Assim como a árvore XGB para regressão, a árvore XGB para classificação se inicia com apenas uma folha que leva todos os resíduos.
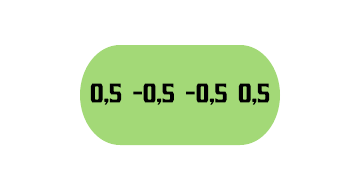
Agora precisamos calcular o Índice de Similaridade para os resíduos. Porém, como estamos usando XGBoost para classificação, temos uma nova fórmula para ele.
\[\hbox{Índice de Similaridade} = \frac{\left( \sum\limits_{i=1}^{n} \hbox{Resíduo}_i \right)^{2}}{\sum\limits_{i=1}^{n} \left[ \hbox{Probabilidade Prévia}_i \times \left( 1 - \hbox{Probabilidade Prévia}_i \right) \right] + \lambda}\]Veja que o numerador da fórmula para classificação é igual ao da fórmula para regressão. E assim como para regressão, o denominador contém $\lambda$, o parâmetro de regularização.
Note que, para o nosso exemplo, o numerador do Índice de Similaridade para a folha resultará em 0, pois nós somamos os resíduos antes de elevá-los ao quadrado, o que faz com que eles se cancelem.
\[\left( \sum\limits_{i=1}^{n} \hbox{Resíduo}_i \right)^{2} = (0,5 - 0,5 - 0,5 + 0,5)^{2} = 0 \Rightarrow \hbox{Índice de Similaridade} = 0\]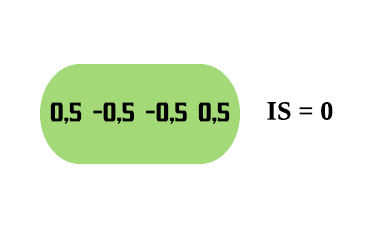
Vamos tentar melhorar o Índice dividindo os resíduos em 2 grupos diferentes. Para isso temos que testar todos os possíveis separadores para os dados e escolher o que tiver o maior ganho. Vamos começar com o primeiro: a média entre os 2 menores valores da variável “Apps”.
ordenados = sort(college$Apps)
mean(ordenados[1:2])
## [1] 1889.5
Assim, os resíduos que possuem Apps < 1889,5 vão para a esquerda, e os com Apps > 1889,5 vão para a direita.
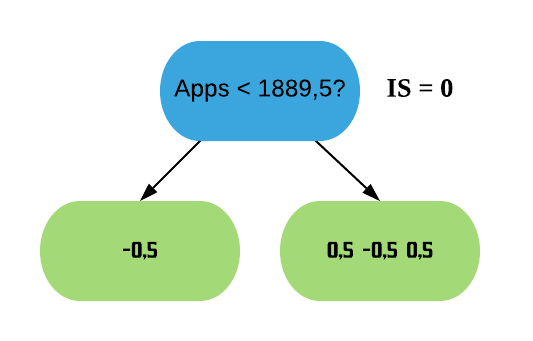
Agora vamos calcular o Índice de Similaridade para as duas folhas. Como estamos construindo nossa primeira árvore, a Probabilidade Prévia para todos os resíduos é a predição da folha inicial (0,5). Para simplificar as contas, vamos utilizar o valor padrão de $\lambda$, $\lambda$ = 0. Contudo, sabemos da regressão que o $\lambda$ reduz o Índice de Similaridade, o que consequentemente diminui o Ganho e assim torna as folhas mais fáceis de serem podadas, o que ajuda a previnir o sobreajuste.
\[\hbox{IS}_\hbox{folha da esquerda} = \frac{(-0,5)^{2}}{0,5 \times (1-0,5)} = 1.\] \[\hbox{IS}_\hbox{folha da direita} = \frac{(-0,5+0,5+0,5)^{2}}{[0,5 \times (1-0,5)] + [0,5 \times (1-0,5)] + [0,5 \times (1-0,5)]} = 0,33.\]Agora podemos calcular o ganho:
\[\hbox{Ganho} = \hbox{IS}_\hbox{folha da esquerda} + \hbox{IS}_\hbox{folha da direita} - \hbox{IS}_{\hbox{raiz}} = 1 + 0,33-0 = 1,33.\]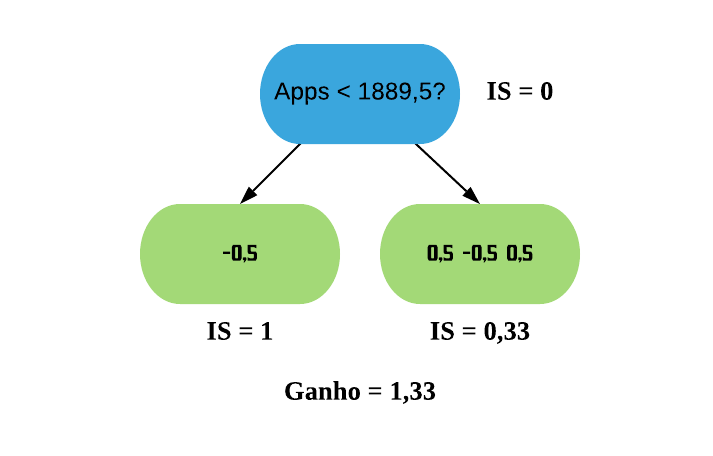
Agora vamos realizar os mesmos cálculos para os próximos 2 separadores: a média entre o segundo e o terceiro valor e a média entre o terceiro e o quarto valor da variável “Apps”.
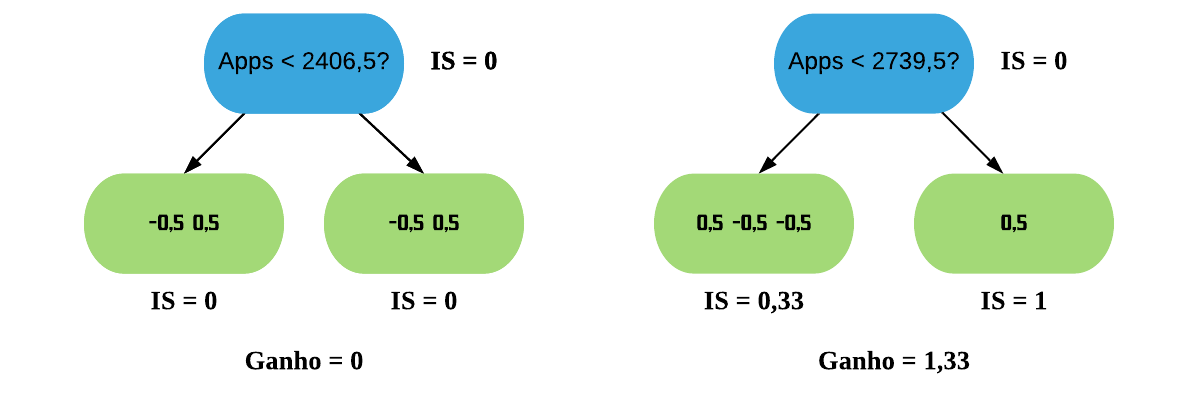
Podemos ver que o maior ganho é tanto o da divisão por “Apps < 1889,5?” quanto o da divisão por “Apps < 2739,5?”, que deram exatamente iguais. Assim, podemos usar qualquer um dos 2 para ser a raiz da árvore XGB. Vamos ficar com o último.
O próximo passo agora é ramificar a folha da esquerda para darmos continuidade à nossa árvore. Novamente, vamos limitar a profundidade dela em 2.
A árvore XGB fica, então, da seguinte forma:
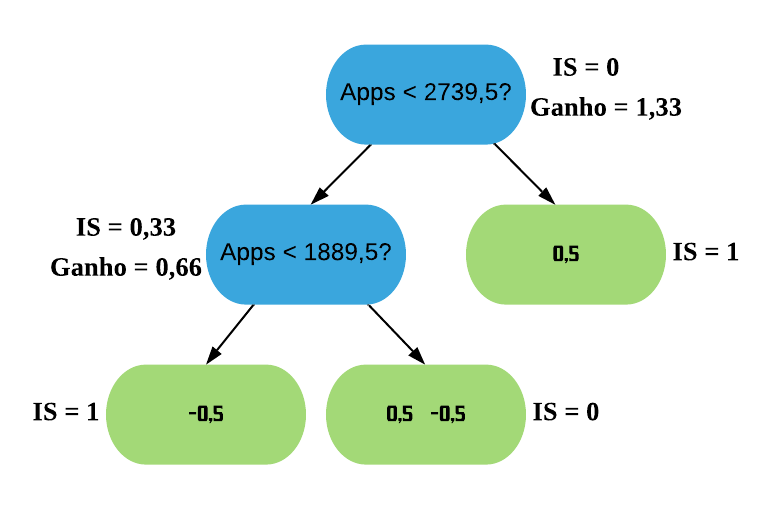
Assim, terminamos de construir a árvore XGB. Porém, é importante saber que o XGBoost possui uma forma de determinar um número mínimo de resíduos permitido em cada folha da árvore. Ele faz isso calculando o Cover das folhas.
\[\hbox{Cover} = \sum\limits_{i=1}^{n} \left[ \hbox{Probabilidade Prévia}_i \times \left( 1 - \hbox{Probabilidade Prévia}_i \right) \right]\]Note que o Cover é definido pelo denominador do Índice de Similaridade sem o $\lambda$. O valor default é de que o Cover seja no mínimo 1, ou seja, se o Cover de uma folha der menor que 1, o XGBoost não permite que ela exista. Se der maior ou igual a 1, ela pode permanecer na árvore.
Calculando o Cover das nossas duas últimas folhas, temos que:
-
Cover da 1ª folha = $0,5 \times (1-0,5) = 0,25$;
-
Cover da 2ª folha = $0,5 \times (1-0,5) + 0,5 \times (1-0,5) = 0,5$.
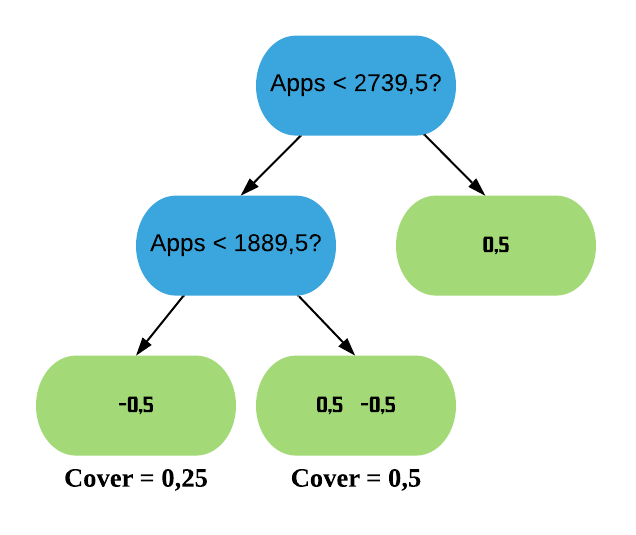
Como o Cover de ambas as folhas são menores do que 1, o XGBoost não as permite permanecer na árvore. Logo, vamos removê-las. A árvore fica, então, da seguinte forma:
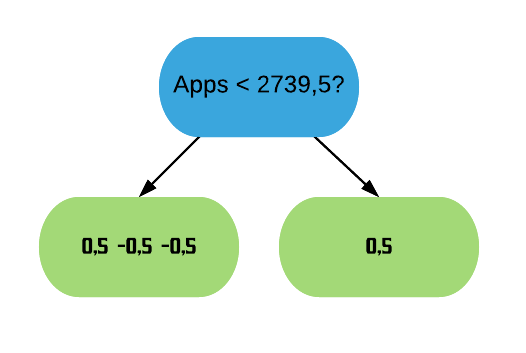
Calculando agora o Cover das duas folhas, obtemos:
-
Cover da 1ª folha = $0,5 \times (1-0,5) + 0,5 \times (1-0,5) + 0,5 \times (1-0,5) = 0,75$;
-
Cover da 2ª folha = $0,5 \times (1-0,5) = 0,25$.
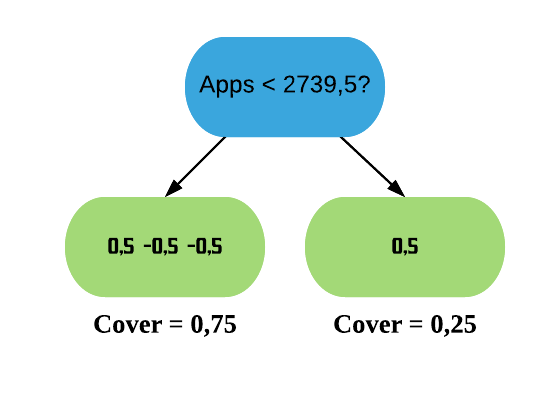
Como o Cover de ambas as folhas também são menores do que 1, o XGBoost também não as permite permanecer na árvore. Assim, só nos resta a raiz. Mas isso também é um problema, pois o XGBoost requer árvores que sejam maiores do que apenas a raiz. Dessa forma, vamos fixar o valor mínimo para o Cover como 0. Assim podemos permanecer com nossa árvore XGB anterior.
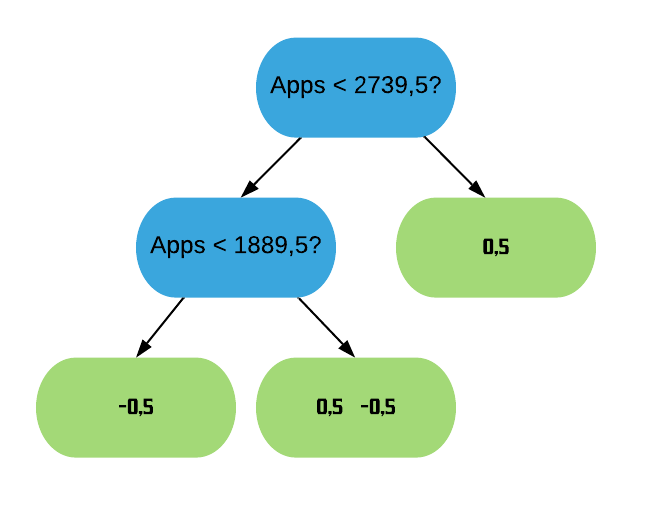
OBS: Quando estamos utilizando XGBoost para regressão usamos a seguinte fórmula para o Índice de Similaridade:
\[\hbox{Índice de Similaridade} = \frac{\left( \sum\limits_{i=1}^{n} \hbox{Resíduo}_i \right)^{2}}{\hbox{Número de Resíduos} + \lambda}\]Logo, o Cover de uma folha é dado por:
\[\hbox{Cover} = \hbox{Número de Resíduos}\]Como o default do Cover é 1, isso significa que podemos ter até 1 resíduo por folha. Em outras palavras, o Cover não tem efeito na construção da árvore. Por conta disso ele não foi utilizado anteriormente em XGBoost para regressão.
Agora vamos entrar na parte de como podar a árvore. Ela é feita exatamente como na regressão, nós podamos com base na diferença entre o Ganho associado ao nó e $\gamma$. Para esse exemplo, vamos fixar $\gamma = 0,5$.
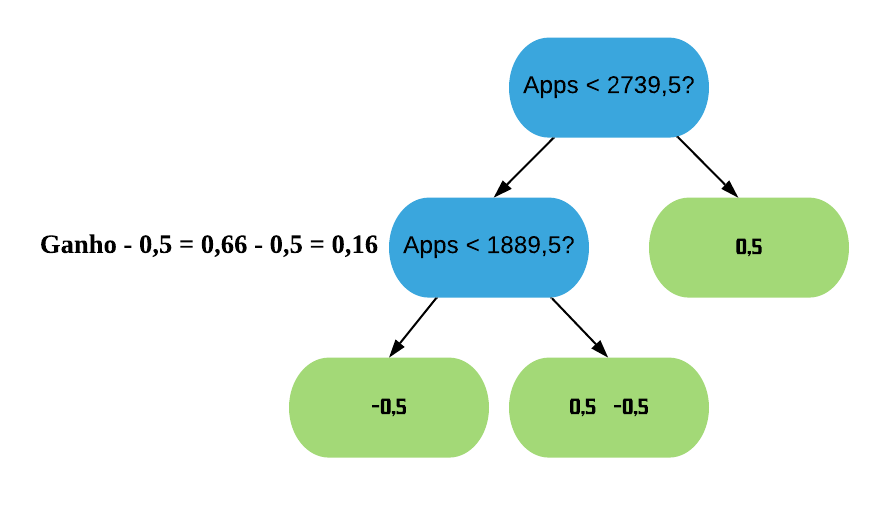
Como a diferença resultou em um número positivo, não podamos o nó. Logo, não precisamos calcular essa diferença para o nó raiz e nossa árvore permanece a mesma. Note que se tivéssemos fixado, por exemplo, $\gamma = 1,5$, todos os nós seriam podados e nos restaria apenas a predição inicial. É necessário cuidado na escolha do $\gamma$.
Obtida a árvore final, vamos calcular os valores de saída que as folhas terão.
\[\hbox{Valores de Saída} = \frac{\sum\limits_{i=1}^{n} \hbox{Resíduo}_i}{\sum\limits_{i=1}^{n} \left[ \hbox{Probabilidade Prévia}_i \times \left( 1 - \hbox{Probabilidade Prévia}_i \right) \right] + \lambda}\]Note que a fórmula é bem parecida com a do Índice de Similaridade, o que muda é apenas o fato de que o numerador não está ao quadrado. Novamente vamos utilizar o valor padrão para $\lambda$, 0.

Agora que construímos nossa primeira árvore podemos realizar predições. Assim como no XGBoost para regressão, o XGBoost para classificação faz novas predições começando com a predição inicial e somando com o resultado da árvore XGB escalado pela taxa de aprendizado. Porém, assim como com o Gradiente Boosting para classificação, precisamos converter a predição inicial, que é uma probabilidade, para log(chances). A fórmula para converter probabilidades para chances é dada por:
\[\frac{p}{1-p} = \hbox{chances}\]Logo, podemos obter uma fórmula que converte probabilidades em log(chances), aplicando log dos dois lados da equação.
\[log \left( \frac{p}{1-p} \right) = log(\hbox{chances})\]Então para a predição inicial de 0,5, temos que $\log \left( \frac{0,5}{1-0,5} \right) = log(1) = 0$. Assim, $log(\hbox{chances}) = 0.$ Agora precisamos adicionar esse valor aos valores de saída da árvore XGB multiplicado pela taxa de aprendizado. Essa taxa é chamada de $\varepsilon$ e seu valor padrão é 0,3, o qual iremos usar.
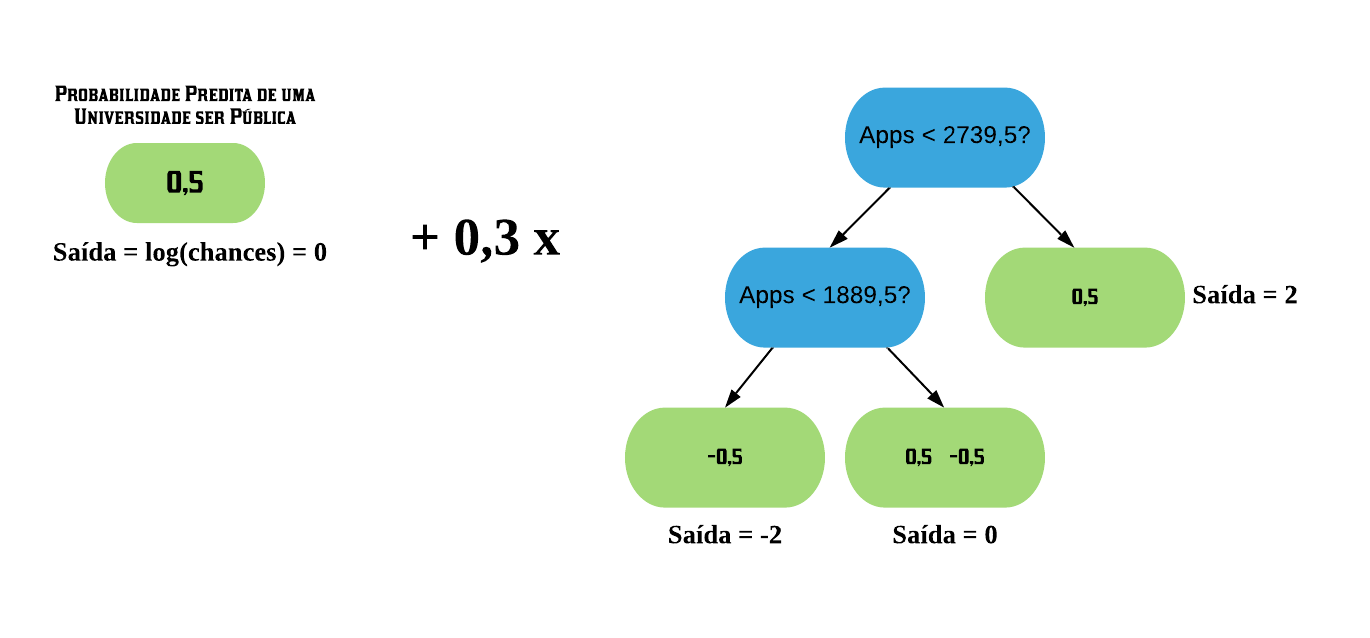
OBS: O que as folhas retornarão após esse cálculo serão os log(chances). É preciso, em seguida, converter para probabilidade também.
Fazendo os cálculos da esquerda para a direita, temos que:
-
Para a 1ª folha, seu valor de saída fica: $0 + 0,3 \times (-2) = -0,6$;
-
Para a 2ª folha, seu valor de saída fica: $0 + 0,3 \times 0 = 0$;
-
Para a 3ª folha, seu valor de saída fica: $0 + 0,3 \times 2 = 0,6$.
Agora para converter esses valores - que são log(chances) - para probabilidade utilizamos a seguinte fórmula:
\[\hbox{Probabilidade} = \frac{e^{log(\hbox{chances})}}{1+e^{log(\hbox{chances})}}\]Fazendo os cálculos, então, da esquerda para a direita:
-
Para a 1ª folha, seu valor de saída fica: $\frac{e^{-0,6}}{1+e^{-0,6}} = 0,35$;
-
Para a 2ª folha, seu valor de saída fica: $\frac{e^{0}}{1+e^{0}} = 0,5$;
-
Para a 3ª folha, seu valor de saída fica: $\frac{e^{0,6}}{1+e^{0,6}} = 0,65$.
Assim, temos as predições da nossa árvore:
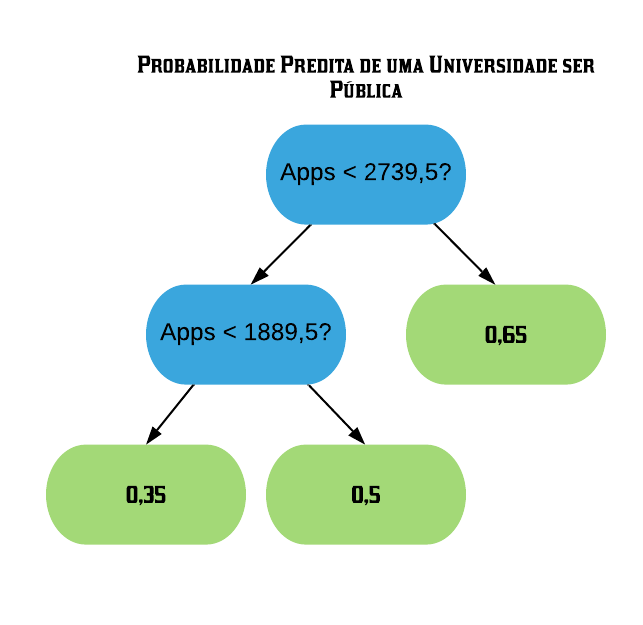
Dessa forma podemos obter novos resíduos utilizando a nova árvore.:
college$Residuos2 = college$Probabilidade-c(0.5,0.35,0.5,0.65)
college
## # A tibble: 4 x 5
## Private Apps Probabilidade Residuos Residuos2
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 No 2119 1 0.5 0.5
## 2 Yes 1660 0 -0.5 -0.35
## 3 Yes 2694 0 -0.5 -0.5
## 4 No 2785 1 0.5 0.35
Observe que os novos resíduos são menores (ou iguais) do que os anteriores, o que significa que estamos indo na direção correta. O próximo passo agora é construir uma nova árvore para os novos resíduos. Note que agora as probabilidades preditas são diferentes (antes era de 0,5 para todos os elementos), o que tornará os cálculos do Índice de Similaridade e dos Valores de Saída mais interessantes, por exemplo. Com a nova árvore construída fazemos novas predições que nos darão resíduos menores ainda. Então construímos uma nova árvore baseada nos novos resíduos e repetimos o processo. Fazemos isso até que os resíduos se tornem super pequenos ou se atingirmos o número máximo de árvores escolhido.
Construindo um classificador com o xgboost
Vamos novamente utilizar o pacote xgboost para construirmos um preditor. Dessa vez iremos construir um classificador e para isso usaremos a base de dados Adult, que se encontra presente no seguinte site: https://archive.ics.uci.edu/ml/index.php. Esse site é um repositório de bases de dados reais, o que torna ele interessante para quem está estudando/trabalhando com aprendizado de máquina.
# Lendo a base de dados como um tibble:
renda =
dplyr::tibble(read.csv(url("https://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data")))
str(renda)
## tibble [32,560 x 15] (S3: tbl_df/tbl/data.frame)
## $ X39 : int [1:32560] 50 38 53 28 37 49 52 31 42 37 ...
## $ State.gov : chr [1:32560] " Self-emp-not-inc" " Private" " Private" " Private" ...
## $ X77516 : int [1:32560] 83311 215646 234721 338409 284582 160187 209642 45781 159449 280464 ...
## $ Bachelors : chr [1:32560] " Bachelors" " HS-grad" " 11th" " Bachelors" ...
## $ X13 : int [1:32560] 13 9 7 13 14 5 9 14 13 10 ...
## $ Never.married: chr [1:32560] " Married-civ-spouse" " Divorced" " Married-civ-spouse" " Married-civ-spouse" ...
## $ Adm.clerical : chr [1:32560] " Exec-managerial" " Handlers-cleaners" " Handlers-cleaners" " Prof-specialty" ...
## $ Not.in.family: chr [1:32560] " Husband" " Not-in-family" " Husband" " Wife" ...
## $ White : chr [1:32560] " White" " White" " Black" " Black" ...
## $ Male : chr [1:32560] " Male" " Male" " Male" " Female" ...
## $ X2174 : int [1:32560] 0 0 0 0 0 0 0 14084 5178 0 ...
## $ X0 : int [1:32560] 0 0 0 0 0 0 0 0 0 0 ...
## $ X40 : int [1:32560] 13 40 40 40 40 16 45 50 40 80 ...
## $ United.States: chr [1:32560] " United-States" " United-States" " United-States" " Cuba" ...
## $ X..50K : chr [1:32560] " <=50K" " <=50K" " <=50K" " <=50K" ...
Essa base possui algumas informações sobre 32.560 indivíduos, tais como: estado civil, raça, sexo, país de origem, entre outras, e a variável de interesse “X..50K”, que indica se o indivíduo tem uma renda maior ou menor/igual do que 50.000 U.M. (unidades monetárias) por ano. Mas antes de começarmos a construção do preditor repare que a base de dados possui variáveis com variância quase-zero.
library(caret)
nearZeroVar(renda, saveMetrics = T)
## freqRatio percentUnique zeroVar nzv
## X39 1.011261 0.224201474 FALSE FALSE
## State.gov 8.931917 0.027641278 FALSE FALSE
## X77516 1.000000 66.483415233 FALSE FALSE
## Bachelors 1.440269 0.049140049 FALSE FALSE
## X13 1.440269 0.049140049 FALSE FALSE
## Never.married 1.401985 0.021498771 FALSE FALSE
## Adm.clerical 1.010002 0.046068796 FALSE FALSE
## Not.in.family 1.588752 0.018427518 FALSE FALSE
## White 8.903649 0.015356265 FALSE FALSE
## Male 2.022932 0.006142506 FALSE FALSE
## X2174 86.020173 0.365479115 FALSE TRUE
## X0 153.668317 0.282555283 FALSE TRUE
## X40 5.397659 0.288697789 FALSE FALSE
## United.States 45.363919 0.128992629 FALSE TRUE
## X..50K 3.152532 0.006142506 FALSE FALSE
Podemos ver que as variáveis “X2174”, “X0” e “United.States” são as que possuem variância quase-zero, o que significa que elas não trarão muita informação ao modelo, pois possuem os mesmos valores ou mesmas classificações para muitos indivíduos.
hist(renda$X2174, main = "Histograma da variável X2174", xlab = "Variável X2174",
ylab = "Frequência", col = "blue")
hist(renda$X0, main = "Histograma da variável X0", xlab = "Variável X0",
ylab = "Frequência", col = "lightblue")
# Tabela com as observações da variável "United.States":
# Repare que a grande maioria dos indivíduos (29.169 de 32.560) é proveniente dos Estados Unidos.
table(renda$United.States)
##
## ? Cambodia Canada China
## 583 19 121 75
## Columbia Cuba Dominican-Republic Ecuador
## 59 95 70 28
## El-Salvador England France Germany
## 106 90 29 137
## Greece Guatemala Haiti Holand-Netherlands
## 29 64 44 1
## Honduras Hong Hungary India
## 13 20 13 100
## Iran Ireland Italy Jamaica
## 43 24 73 81
## Japan Laos Mexico Nicaragua
## 62 18 643 34
## Outlying-US(Guam-USVI-etc) Peru Philippines Poland
## 14 31 198 60
## Portugal Puerto-Rico Scotland South
## 37 114 12 80
## Taiwan Thailand Trinadad&Tobago United-States
## 51 18 19 29169
## Vietnam Yugoslavia
## 67 16
Dessa forma, vamos remover essas variáveis do banco de dados.
# Vetor com todas as variáveis com variância quase-zero:
nzv = nearZeroVar(renda)
# Removendo do banco de dados:
renda = renda[, -nzv]
Agora precisamos nos atentar a um fator importante da função xgboost: ela só aceita bases de dados com variáveis numéricas. Isso é um problema para a nossa base pois ela possui variáveis do tipo factor. O que fazer nesse caso? A resposta para essa pergunta é simples: vamos transformar essas variáveis em variáveis dummies.
# Criando as variáveis dummies:
dummies = dummyVars(~ X..50K + State.gov + Bachelors + Never.married + Adm.clerical +
Not.in.family + White + Male, data = renda, fullRank = T)
# Aplicando ao modelo:
Dummies = predict(dummies, newdata = renda)
# Anexando aos dados:
renda = cbind(renda, Dummies)
# Excluindo as variáveis categóricas do banco de dados:
renda = dplyr::select(renda, -c(X..50K, State.gov, Bachelors, Never.married,
Adm.clerical, Not.in.family, White, Male))
head(renda)
## X39 X77516 X13 X40 X..50K >50K State.gov Federal-gov State.gov Local-gov State.gov Never-worked State.gov Private
## 1 50 83311 13 13 0 0 0 0 0
## 2 38 215646 9 40 0 0 0 0 1
## 3 53 234721 7 40 0 0 0 0 1
## 4 28 338409 13 40 0 0 0 0 1
## 5 37 284582 14 40 0 0 0 0 1
## 6 49 160187 5 16 0 0 0 0 1
## State.gov Self-emp-inc State.gov Self-emp-not-inc State.gov State-gov State.gov Without-pay Bachelors 11th
## 1 0 1 0 0 0
## 2 0 0 0 0 0
## 3 0 0 0 0 1
## 4 0 0 0 0 0
## 5 0 0 0 0 0
## 6 0 0 0 0 0
## Bachelors 12th Bachelors 1st-4th Bachelors 5th-6th Bachelors 7th-8th Bachelors 9th Bachelors Assoc-acdm
## 1 0 0 0 0 0 0
## 2 0 0 0 0 0 0
## 3 0 0 0 0 0 0
## 4 0 0 0 0 0 0
## 5 0 0 0 0 0 0
## 6 0 0 0 0 1 0
## Bachelors Assoc-voc Bachelors Bachelors Bachelors Doctorate Bachelors HS-grad Bachelors Masters Bachelors Preschool
## 1 0 1 0 0 0 0
## 2 0 0 0 1 0 0
## 3 0 0 0 0 0 0
## 4 0 1 0 0 0 0
## 5 0 0 0 0 1 0
## 6 0 0 0 0 0 0
## Bachelors Prof-school Bachelors Some-college Never.married Married-AF-spouse Never.married Married-civ-spouse
## 1 0 0 0 1
## 2 0 0 0 0
## 3 0 0 0 1
## 4 0 0 0 1
## 5 0 0 0 1
## 6 0 0 0 0
## Never.married Married-spouse-absent Never.married Never-married Never.married Separated Never.married Widowed
## 1 0 0 0 0
## 2 0 0 0 0
## 3 0 0 0 0
## 4 0 0 0 0
## 5 0 0 0 0
## 6 1 0 0 0
## Adm.clerical Adm-clerical Adm.clerical Armed-Forces Adm.clerical Craft-repair Adm.clerical Exec-managerial
## 1 0 0 0 1
## 2 0 0 0 0
## 3 0 0 0 0
## 4 0 0 0 0
## 5 0 0 0 1
## 6 0 0 0 0
## Adm.clerical Farming-fishing Adm.clerical Handlers-cleaners Adm.clerical Machine-op-inspct Adm.clerical Other-service
## 1 0 0 0 0
## 2 0 1 0 0
## 3 0 1 0 0
## 4 0 0 0 0
## 5 0 0 0 0
## 6 0 0 0 1
## Adm.clerical Priv-house-serv Adm.clerical Prof-specialty Adm.clerical Protective-serv Adm.clerical Sales
## 1 0 0 0 0
## 2 0 0 0 0
## 3 0 0 0 0
## 4 0 1 0 0
## 5 0 0 0 0
## 6 0 0 0 0
## Adm.clerical Tech-support Adm.clerical Transport-moving Not.in.family Not-in-family Not.in.family Other-relative
## 1 0 0 0 0
## 2 0 0 1 0
## 3 0 0 0 0
## 4 0 0 0 0
## 5 0 0 0 0
## 6 0 0 1 0
## Not.in.family Own-child Not.in.family Unmarried Not.in.family Wife White Asian-Pac-Islander White Black White Other
## 1 0 0 0 0 0 0
## 2 0 0 0 0 0 0
## 3 0 0 0 0 1 0
## 4 0 0 1 0 1 0
## 5 0 0 1 0 0 0
## 6 0 0 0 0 1 0
## White White Male Male
## 1 1 1
## 2 1 1
## 3 0 1
## 4 0 0
## 5 1 0
## 6 0 0
Note que agora todas as nossas variáveis são numéricas e, portanto, a base está pronta para construirmos o preditor. Como sempre, vamos começar dividindo-a em amostra treino e amostra teste.
set.seed(11)
noTreino = createDataPartition(renda$`X..50K >50K`, p = 0.75, list = F)
# Lembre-se que temos que transformar a base em uma matriz:
renda = as.matrix(renda)
treino = renda[noTreino, -5]
treino_label = renda[noTreino, 5]
teste = renda[-noTreino, -5]
teste_label = renda[-noTreino, 5]
Agora vamos usar a função xgboost() para criar o modelo.
library(xgboost)
set.seed(11)
modelo = xgboost(data = treino, label = treino_label, lambda = 1, gamma = 0, eta = 0.3,
nrounds = 500, objective = "binary:logistic", verbose = 0, max_depth = 3)
# Fazendo a predição:
predicao = predict(modelo, teste)
head(predicao)
## [1] 0.846276224 0.001679021 0.220495090 0.008715384 0.843290508 0.730734646
O modelo retorna probabilidades, então devemos criar um classificador. Vamos criar um bem simples, da seguinte forma:
- Probabilidade acima de 0,5: consideramos que a renda do indivíduo é maior do que 50.000;
- Probabilidade abaixo de 0,5: consideramos que a renda do indivíduo é menor ou igual a 50.000.
classificador = as.numeric(predicao>=0.5)
# Utilizando a matriz de confusão para avaliar o modelo:
confusionMatrix(data = as.factor(classificador), reference = as.factor(teste_label), positive = "1")
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 5654 794
## 1 564 1128
##
## Accuracy : 0.8332
## 95% CI : (0.8249, 0.8412)
## No Information Rate : 0.7639
## P-Value [Acc > NIR] : < 0.00000000000000022
##
## Kappa : 0.5176
##
## Mcnemar's Test P-Value : 0.0000000005159
##
## Sensitivity : 0.5869
## Specificity : 0.9093
## Pos Pred Value : 0.6667
## Neg Pred Value : 0.8769
## Prevalence : 0.2361
## Detection Rate : 0.1386
## Detection Prevalence : 0.2079
## Balanced Accuracy : 0.7481
##
## 'Positive' Class : 1
##
Podemos usar o pacote DiagrammeR para visualizarmos as árvores construídas pelo modelo. Para isso basta utilizarmos a função xgb.plot.tree() e no argumento trees escolhermos a(s) árvore(s) desejada(s).
library(DiagrammeR)
# Visualizando a segunda árvore construída:
xgb.plot.tree(model = modelo, trees = 2)
## Error in loadNamespace(name): there is no package called 'webshot'
Outros Métodos
Neste capítulo estudaremos alguns métodos não baseados em árvores que também são muito importantes e utilizados em machine learning: Support Vector Machine (SVM) e K-Nearest Neighbors (KNN). Veremos como os modelos funcionam na teoria com alguns exemplos e em seguida iremos implementá-los computacionalmente utilizando a linguagem R.
*Support Vector Machine (SVM)
O Support Vector Machine - ou Máquina de Vetores de Suporte - é um algoritmo de aprendizado supervisionado que analisa os dados e os divide em diferentes grupos, de acordo com seus padrões, para assim classificar as observações. É mais utilizado em problemas de classificação, o qual será o maior foco deste capítulo, mas também pode ser utilizado para regressão.
em Classificação
Para entender como esse método funciona, vamos utilizar a seguinte situação: queremos verificar se as vendas de um produto em diferentes mercados foram altas ou baixas baseado nos gastos com publicidade desse produto para TV. Para tal temos a amostra treino abaixo:
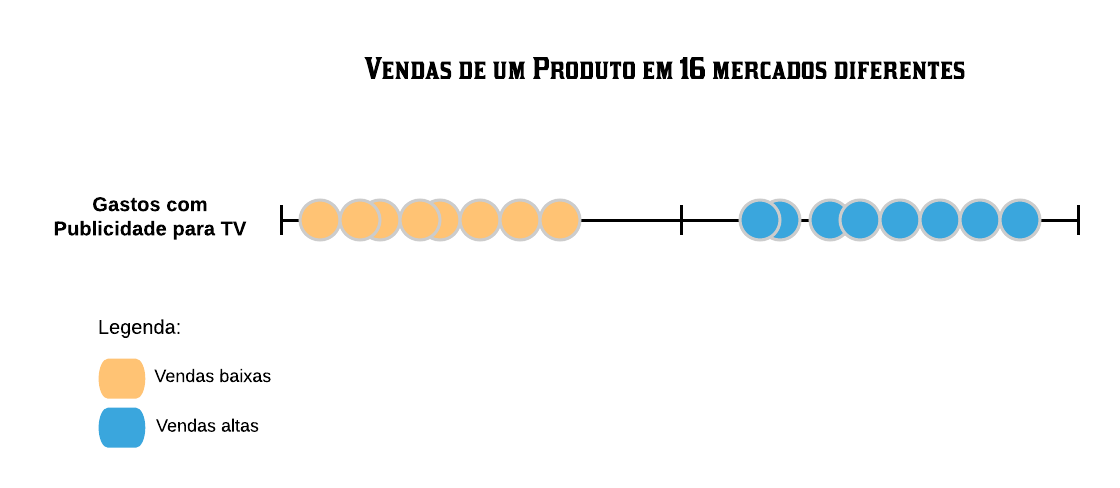
Podemos observar que os mercados que possuíram um maior investimento em publicidade tiveram maiores vendas, estando naturalmente agrupados mais à direita do gráfico. O objetivo do algoritmo é criar um classificador no formato de um separador, ou seja, um ponto que melhor separe os dados entre os que foram classificados como baixas ou altas vendas, de acordo com os gastos com publicidade.
Esse separador é criado como sendo o ponto médio entre os elementos de cada grupo. Dessa forma, é natural perceber que o melhor separador para a amostra é a média entre o mercado que obteve a maior venda dentre os que tiveram baixas vendas e o mercado que obteve a menor venda dentre os que tiveram altas vendas (as bordas de cada agrupamento).
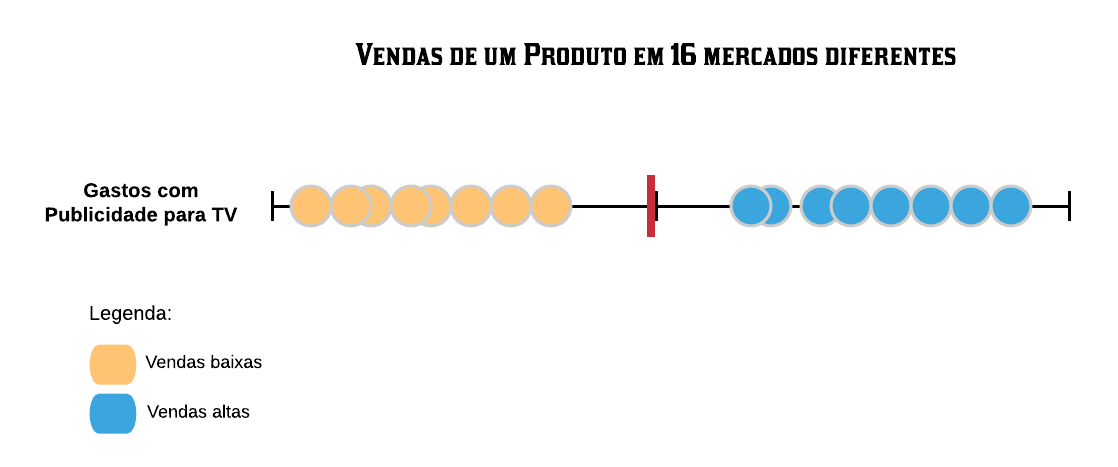
Assim, quando novas amostras chegarem para serem analisadas, podemos classificá-las de acordo com nosso classificador. Se ela tiver à esquerda dele será classificada como vendas baixas e se tiver à direita como vendas altas.
Definição 1: a menor distância entre o classificador e as observações utilizadas para calculá-lo é chamada de margem.
Como nosso classificador está no ponto médio entre os dois elementos da borda de cada grupo, a margem é a distância de uma dessas observações até ele. Caso ele estivesse mais à esquerda, por exemplo, a margem seria a distância entre ele e o elemento que está na borda do agrupamento das vendas baixas.
Definição 2: o classificador que dá a maior margem para fazer classificações é chamado de classificador de margem máxima.
O classificador de margem máxima performa bem em bases onde os elementos estejam bem agrupados, mas ele se torna um classificador falho quando a base possui outliers. Por exemplo, se um dos mercados do nosso conjunto treino gastou pouco com publicidade para TV, mas obteve vendas altas, o classificador de margem máxima estaria muito próximo ao agrupamento das vendas baixas.
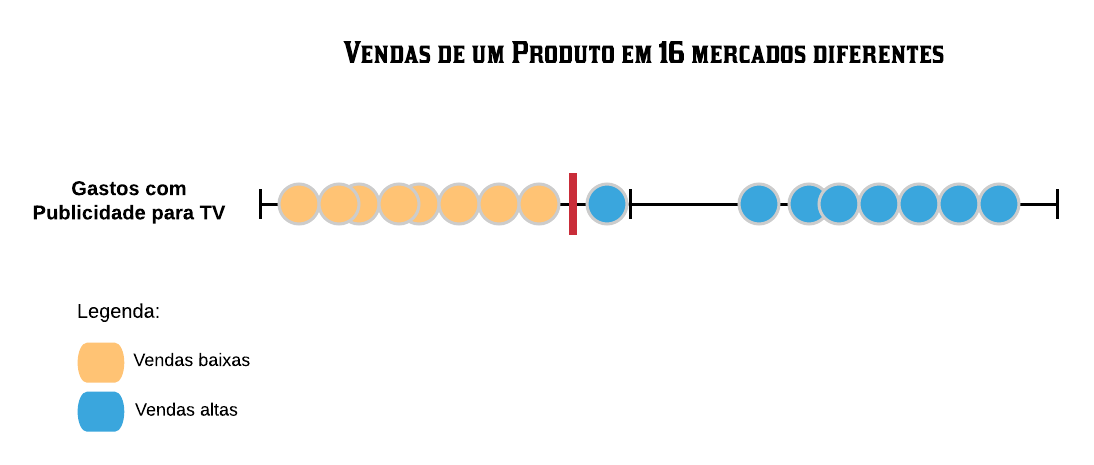
Dessa forma, novas amostras à direita do classificador seriam classificadas como vendas altas, mesmo que elas estivessem mais próximas ao grupo das vendas baixas. Ou seja, isso implicaria em muitos erros de classificação.
Para melhorarmos essa situação precisamos de um classificador que não seja tão sensível a outliers. Para isso teremos que permitir alguns erros de classificação no conjunto treino, aumentando o viés do classificador para que, assim, quando o algoritmo receber novas amostras, a variância dele seja menor.
Definição 3: Quando é utilizado um classificador que permite erros de classificação, a distância entre ele e os elementos utilizados para obtê-lo é chamada de margem suave.
Como temos várias margens suaves a se considerar, o algoritmo utiliza cross validation para determinar qual é a melhor delas, escolhendo o melhor separador para ser utilizado.
Definição 4: As observações utilizadas para calcular a margem suave são chamadas de support vectors (vetores de suporte).
Definição 5: O classificador escolhido quando é utilizado a melhor margem suave é chamado de classificador de margem suave ou support vector classifier (classificador de vetor de suporte).
Vamos adicionar agora mais uma variável ao nosso problema. Queremos analisar as vendas do produto com base nos gastos com publicidade para TV e nos gastos com publicidade para o rádio.
library(readxl)
vendas = read_excel("sales.xlsx")
vendas
## # A tibble: 10 x 4
## TV radio newspaper sales
## <chr> <chr> <chr> <chr>
## 1 8.6 2.1 1 low
## 2 75.5 10.8 6 low
## 3 107.4 14 10.9 low
## 4 120.2 19.6 11.6 low
## 5 120.5 28.5 14.2 low
## 6 191.1 28.7 18.2 high
## 7 248.4 30.2 20.3 high
## 8 281.4 39.6 55.8 high
## 9 283.6 42 66.2 high
## 10 290.7 4.1 8.5 high
Note que à medida que os gastos com publicidade nas duas mídias aumentam, as vendas do produto também aumentam. Vamos verificar graficamente o comportamento dessas variáveis.
library(dplyr)
library(ggplot2)
# Transformando a variável resposta em fator:
vendas$sales = as.factor(vendas$sales)
# Transformando as demais variáveis em números:
vendas = mutate_if(vendas, is.character, as.numeric)
# Desenhando o gráfico:
vendas %>% ggplot(aes(x = TV, y = radio, color = sales)) + geom_point(size = 3) + theme_minimal() +
ggtitle("Vendas de um Produto em Diferentes Mercados") + xlab("Publicidade para TV") +
ylab("Publicidade para Radio") + scale_color_manual(values = c("blue", "orange"))
Repare que as amostras, assim como anteriormente, estão agrupadas em clusters. E, novamente, para escolher o melhor classificador, o algoritmo irá utilizar cross validation para determinar qual é a melhor margem suave. Como o problema possui duas variáveis, o support vector classifier será uma linha dividindo os dois grupos.
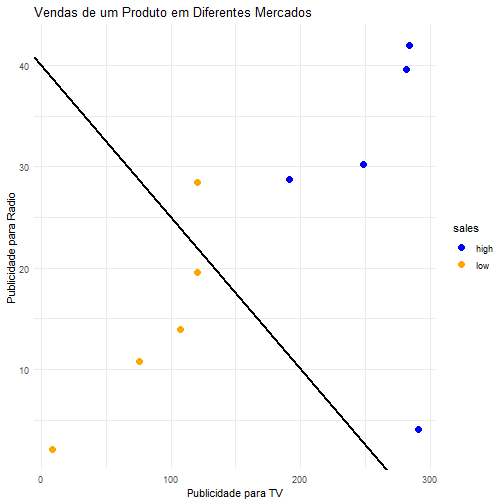
Assim, as novas amostras que estiverem à direita da linha serão classificadas como vendas altas, e as que estiverem à esquerda como vendas baixas.
Agora vamos adicionar uma terceira variável, ou seja, vamos levar em conta também a terceira coluna da base de dados, os gastos com publicidade para os jornais. Vamos verificar o comportamento das variáveis graficamente.
# Pacote para plotar gráfico de pontos em 3 dimensões:
library(scatterplot3d)
# Escolhendo as cores dos pontos:
cores = c("blue", "orange")
# Colorindo-os de acordo com as classificações das vendas:
cores = cores[as.numeric(vendas$sales)]
# Desenhando o gráfico:
scatterplot3d(vendas$TV, vendas$radio, vendas$newspaper, color = cores, pch = 19,
xlab = "Publicidade para TV", ylab = "Publicidade para Radio",
zlab = "Publicidade para Jornais", main = "Vendas de um Produto em Diferentes Mercados")
# Adicionando legenda ao gráfico:
legend("top", legend = c("Vendas baixas", "Vendas altas"), col = c("orange", "blue"), pch = 19,
horiz = T)
Note que, novamente, os dados estão agrupados naturalmente. Quando a base de dados é tridimensional, o classificador de vetor de suporte é um plano e classificamos as novas observações determinando em qual lado do plano elas se encontram.
E se a base de dados possuí-se mais uma variável, por exemplo, publicidade para internet? Nesse caso, o classificador seria um hiperplano. Matematicamente, em um espaço p-dimensional, um hiperplano é definido como um subespaço plano de dimensão p-1. Ele é a generalização do plano em diferentes números de dimensões. Quando a base é unidimensional, o classificador de vetor de suporte é um ponto, ou seja, um hiperplano de dimensão 0. Quando a base é bidimensional, o classificador de vetor de suporte é uma linha, ou seja, um hiperplano de dimensão 1. E quando a base é tridimensional, o classificador de vetor de suporte é um plano comum (hiperplano de dimensão 2). Então, generalizando, quando a base é p-dimensional, o classificador de vetor de suporte é um hiperplano de dimensão p-1.
Em suma, support vector classifiers são ótimos classificadores, mas eles só performam bem em base de dados linearmente separáveis. Por exemplo, suponha que a amostra abaixo seja o nosso conjunto treino.
v = read_excel("sales2.xlsx")
v
## # A tibble: 16 x 2
## TV sales
## <chr> <chr>
## 1 230.1 high
## 2 44.5 low
## 3 17.2 high
## 4 151.5 low
## 5 180.8 low
## 6 8.7 high
## 7 57.5 low
## 8 120.2 low
## 9 8.6 high
## 10 199.8 high
## 11 66.1 low
## 12 214.7 high
## 13 23.8 high
## 14 97.5 low
## 15 204.1 high
## 16 195.4 high
# Transformando a variável de interesse em fator:
v$sales = as.factor(v$sales)
# Transformando a variável com os valores dos gastos com publicidade para TV em números:
v$TV = as.numeric(v$TV)
# Gráfico das vendas baseado na puclicidade para TV:
v %>% ggplot(aes(x = TV, y = 0, color = sales)) + geom_point(size = 3) + xlab("Publicidade para TV") +
ggtitle("Vendas de um Produto em Diferentes Mercados") + scale_color_manual(values = c("blue", "orange")) +
theme(axis.title.y = element_blank(), axis.text.y = element_blank(), axis.ticks.y = element_blank(),
panel.background = element_blank())
Utilizar um classificador de vetor de suporte seria inviável nesse caso, visto que onde quer que ele se encontre existiriam muitos erros de classificação. Para esse tipo de situação em que os dados não são linearmente separáveis, que é o mais habitual de se encontrar na realidade, precisamos utilizar support vector machines.
Definição 6: Support vector machine (máquina de vetores de suporte) é uma extensão do support vector classifier que resulta da ampliação do espaço característico de um jeito específico, utilizando kernels.
Em outras palavras, o que o support vector machine (máquina de vetores de suporte) faz é aumentar a dimensão da nossa base de dados por meio de funções (conhecidas como kernels) para que a base se torne linearmente separável, tornando possível o uso dos classificadores de vetores de suporte. Por exemplo, vamos criar uma nova variável definida como sendo os valores da variável que representa os gastos com publicidade para TV elevados ao quadrado.
# Adicionando a nova variável com os valores elevados ao quadrado:
v = v %>% mutate(TV2 = TV**2)
# Gráfico das vendas baseado nos valores da publicidade e publicidade ao quadrado:
v %>% ggplot(aes(x = TV, y = TV2, color = sales)) + geom_point(size = 3) + xlab("Publicidade para TV") +
ylab("Publicidade para TV ao quadrado") + ggtitle("Vendas de um Produto em Diferentes Mercados") +
scale_color_manual(values = c("blue", "orange")) + theme_minimal()
Repare que, aumentando a dimensão da nossa base de 1 para 2 com a transformação que eleva os valores da publicidade ao quadrado, a nossa base agora se tornou linearmente separável. Então podemos utilizar um classificador de vetor de suporte no formato de uma linha para separar os dados.
Assim, quando uma nova observação chegar, será calculado o valor da sua publicidade para TV ao quadrado e, de acordo com o lugar que esse valor ficar em relação a linha, a observação será classificada como vendas baixas ou vendas altas. E, resumidamente, é dessa forma que o SVM opera para todas as bases de dados.
Por último, mas não menos importante, para escolher as funções que tornem a base possível de ser separada, o SVM utiliza as funções kernel.
A função kernel é uma função que computa as relações entre cada par de observações, e essas relações são utilizadas afim de encontrar um classificador de vetor de suporte. Ela é a responsável por aumentar a dimensão da base de dados por meio das transformações que a tornem linearmente separável.
Denota-se a função kernel como $K(x,y)$, onde x e y se referem a duas diferentes observações no conjunto de dados. O kernel utilizado no exemplo acima foi o polinomial. Juntamente com esse, os mais utilizados são os lineares, radiais e sigmoid. Um parâmetro presente em todos os kernels (exceto o linear) é o $\gamma$, cuja função é escalar a quantidade de influência que duas observações têm uma sobre a outra. Quanto maior o $\gamma$, menor a influência.
Linear:
\[K(x,y) = x^{T}y\]Nada mais é do que um produto vetorial entre as observações. É utilizados quando a base de dados já é, naturalmente, linearmente separável.
Polinomial:
\[K(x,y) = [\gamma(x^{T}y) + c]^{d}\]onde:
-
c é o parâmetro de penalidade do modelo, o parâmetro que controla seu ajuste. Para grandes valores de c, o algoritmo não pode classificar observações do conjunto treino de forma errada.
-
d determina o grau do polinômio.
Como o nome sugere, ele utiliza uma transformação polinomial nos dados para torná-los linearmente separáveis. Para escolher os valores do c e do d o mais recomendado é utilizar cross validation.
Radial:
O kernel radial, também conhecido como kernel RBF (radial basis function), é comumente o kernel mais utilizado. Ele encontra classificadores de vetores de suporte em infinitas dimensões, por isso não é possível visualizá-lo graficamente. Seu comportamento se resume a separar as amostras do conjunto treino em círculos, de acordo com seus agrupamentos. Assim, a classificação das novas observações é altamente influenciada pelas observações que estão próximas a ela, e poucamente influenciada pelas que estão distantes. Sua fórmula é dada por:
\[K(x,y) = e^{-\gamma||x-y||^{2}}\]| onde $ | x-y | $ é a norma (ou comprimento) do vetor $x-y$. |
Sigmoid:
O kernel sigmoid, também conhecido como kernel da tangente hiperbólica, é bastante popular por ser proveniente dos estudos das redes neurais, e por ter um bom desempenho no geral. Sua fórmula é dada por:
\[K(x,y) = tanh(\gamma[x^{T}y] + c)\]onde, assim como no kernel polinomial, o parâmetro c é o parâmetro de penalidade do modelo, o parâmetro que controla seu ajuste.
em Regressão
O support vector machine para regressão - mais conhecido como support vector regression (SVR) - usa os mesmos princípios que o SVM para classificação, com algumas poucas diferenças. Para começar, como não temos classes nos dados, o objetivo não é tentar agrupá-los de acordo com elas, visto que agora o que queremos prever são números reais.
Vamos supor que queremos prever as vendas de um produto em unidades monetárias (U.M.) em diferentes mercados baseado nos gastos com publicidade para TV (em U.M.) que o mercado teve com esse produto. Para tal, suponha que a amostra abaixo seja nossa amostra de treino.
Note que agora é necessário termos um eixo para representar a variável de interesse. Podemos reparar também que, em geral, à medida que os gastos com publicidade aumentam, as vendas também aumentam.
Ao invés de encontrar uma linha para separar os dados, o objetivo do SVR é encontrar uma linha com o objetivo de ajustar os dados sobre ela. A ideia é parecida com a de regressão linear simples, exceto pelo fato de que, ao invés de minimizar a soma dos quadrados dos resíduos, seu objetivo é minimizar a norma do vetor de coeficiente, um assunto que está fora dos escopos deste material. Para mais informações, consulte o livro The Elements of Statistical Learning.
Para definirmos o quanto de erro é aceitável no nosso modelo, utilizamos o parâmetro $\varepsilon$. A figura abaixo apresenta a linha azul que representa a linha de melhor ajuste de acordo com a margem de erro escolhida ($\varepsilon$), representada pelas linhas verdes.
O algoritmo ajusta o modelo da melhor forma possível, mas ainda assim alguns pontos ainda ficam fora da margem de erro. Para definirmos a tolerância que o algoritmo deve ter desse número de pontos que ficam fora da margem utilizamos o parâmetro c. Conforme c aumenta, a tolerância do número de pontos também aumenta, e quando c é pequeno a tolerância também fica pequena.
Dependendo dos valores escolhidos para o $\varepsilon$ e para o c o algoritmo pode não ser capaz de encontrar um regressor para os dados. Por exemplo, se escolhermos um c e um $\varepsilon$ muito pequenos quando as observações são muito dispersas. É preciso cuidado.
Generalizando para maiores dimensões, ao invés do SVR utilizar uma linha para ajustar os dados, ele utiliza hiperplanos. Assim, quando uma nova observação chegar, seu valor de saída será predito de acordo com as coordenadas do hiperplano em que ela se encontra.
SVM com a função svm() do pacote e1071
Vamos utilizar a base de dados mtcars do pacote básico do R. Essa base contém algumas informações de desempenho e design que permitem comparar diferentes modelos de automóveis, como mpg que indica a quantidade de milhas que é possivel percorrer com um galão (miles per gallon), hp que indica a potência em cavalos (horsepower), wt indica o peso em libras (weight) e qsec que indica o tempo em segundo pra percorrer 1/4 de milha (quarter mile time in seconds). Nossa variável de interesse é am que indica se o câmbio é automático ou manual.
library(caret)
data("mtcars")
mtcars$am = factor(mtcars$am, labels = c("automatic","manual"))
head(mtcars)
## mpg cyl disp hp drat wt qsec vs am gear carb
## Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 manual 4 4
## Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 manual 4 4
## Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 manual 4 1
## Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 automatic 3 1
## Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 automatic 3 2
## Valiant 18.1 6 225 105 2.76 3.460 20.22 1 automatic 3 1
set.seed(5)
noTreino = caret::createDataPartition(y = mtcars$am, p = 0.7, list = F)
treino = mtcars[noTreino,]
teste = mtcars[-noTreino,]
Utilizando Kernel linear
Para melhor visualização, vamos utilizar apenas duas variáveis explicativas no começo. Observe essas duas variáveis.
library(ggplot2)
ggplot(data = treino, aes(x = qsec, y = wt, color = am)) +
geom_point(size = 3) +
scale_color_manual(values=c("darkolivegreen3", "brown2")) +
theme_minimal()
Parece ser possível separar as observações em dois grupos, manual e automático, apenas com uma linha. Vamos tentar treinar um modelo de svm linear então. Para isso, utilizaremos a função svm().
library(dplyr); library(e1071)
# treinando o modelo
set.seed(645)
svmfit = e1071::svm(am ~ ., data = select(treino, am, wt, qsec),
kernel = "linear", cost = 1, scale = T)
svmfit
##
## Call:
## svm(formula = am ~ ., data = select(treino, am, wt, qsec), kernel = "linear", cost = 1, scale = T)
##
##
## Parameters:
## SVM-Type: C-classification
## SVM-Kernel: linear
## cost: 1
##
## Number of Support Vectors: 10
Os principais argumentos dessa função são:
- kernel = indica o tipo de kernel. Os mais comuns são ‘linear’, ‘polynomial’ e ‘radial’ (sendo esse último o default).
- cost = quantifica a penalidade associada a uma predição incorreta. Default=1.
- scale = se TRUE (default), padroniza as variáveis.
- gamma = parâmetro usado no cálculo exceto quando o kernel é linear. Default = $\frac{1}{nº colunas\ da\ base}$
- coef0 = parâmetro usado no cálculo quando o kernel é polinomial. Default=0.
- degree = usado quando o kernel é polinomial. Indica o grau do polinômio. Default=3.
# visualizando o modelo
plot(svmfit, select(treino, am, qsec, wt), col=c("cornflowerblue", "darkred"))
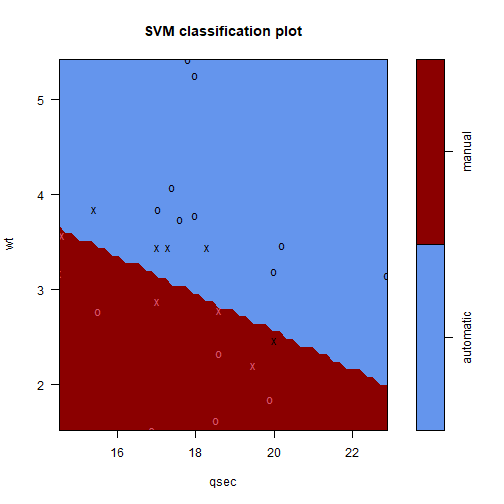
As observações em vermelho, são as rotuladas como manuais, e as pretas como automaticas.
Segundo nosso modelo toda nova observação que estiver acima da linha, parte azul, será classificada/predita como automatico. Caso contrário, classificada como manual.
Por fim, as observações com forma de “X” são as que foram usadas como vetores de suporte (se observar a descrição do modelo, verá que são 9 os vetores de suporte).
Agora, vamos avaliar nosso preditor
# realizando a predicao sob o conjunto de teste
predicao = predict(svmfit, select(teste, am, wt, qsec))
# obtendo a matriz de confusao
confusionMatrix(data = predicao, reference = teste$am)
## Confusion Matrix and Statistics
##
## Reference
## Prediction automatic manual
## automatic 5 0
## manual 0 3
##
## Accuracy : 1
## 95% CI : (0.6306, 1)
## No Information Rate : 0.625
## P-Value [Acc > NIR] : 0.02328
##
## Kappa : 1
##
## Mcnemar's Test P-Value : NA
##
## Sensitivity : 1.000
## Specificity : 1.000
## Pos Pred Value : 1.000
## Neg Pred Value : 1.000
## Prevalence : 0.625
## Detection Rate : 0.625
## Detection Prevalence : 0.625
## Balanced Accuracy : 1.000
##
## 'Positive' Class : automatic
##
# outra forma de obter a precisao
mean(predicao == teste$am)
## [1] 1
Agora, na hora de treinar o modelo, note que utilizamos cost=1. Mas e se esse não for o melhor custo? Podemos utilizar a função tune() também do pacote e1071 para testar vários valores de parâmetros.
library(e1071)
set.seed(645)
tunefit = e1071::tune(svm, am ~ ., data = select(treino, am, qsec, wt),
kernel = "linear",
ranges = list(cost = seq(0.1, 2, length = 10)))
tunefit$best.model
##
## Call:
## best.tune(method = svm, train.x = am ~ ., data = select(treino, am, qsec, wt), ranges = list(cost = seq(0.1,
## 2, length = 10)), kernel = "linear")
##
##
## Parameters:
## SVM-Type: C-classification
## SVM-Kernel: linear
## cost: 0.3111111
##
## Number of Support Vectors: 15
Dessa forma, foram feitos 10 treinamentos (cost = 0.1, 0.31, 0.52, 0.73, 0.94, 1.16, 1.37, 1.58, 1.79, 2) e concluído que o melhor (maior precisão) foi quando o custo era 0.31.
# realizando a predicao sob o conjunto de teste
predicao = predict(tunefit$best.model, select(teste, am, wt, qsec))
# obtendo a matriz de confusao
confusionMatrix(data = predicao, reference = teste$am)
## Confusion Matrix and Statistics
##
## Reference
## Prediction automatic manual
## automatic 5 0
## manual 0 3
##
## Accuracy : 1
## 95% CI : (0.6306, 1)
## No Information Rate : 0.625
## P-Value [Acc > NIR] : 0.02328
##
## Kappa : 1
##
## Mcnemar's Test P-Value : NA
##
## Sensitivity : 1.000
## Specificity : 1.000
## Pos Pred Value : 1.000
## Neg Pred Value : 1.000
## Prevalence : 0.625
## Detection Rate : 0.625
## Detection Prevalence : 0.625
## Balanced Accuracy : 1.000
##
## 'Positive' Class : automatic
##
# outra forma de obter a precisao
mean(predicao == teste$am)
## [1] 1
Utilizando Kernel polinomial
Agora, observe o gráfico novamente
Será que se usarmos uma curva no lugar de uma reta para separar os grupos, teriamos um modelo melhor? Vamos treinar um modelo usando o kernel polinomial.
set.seed(987)
svmfit.p = svm(am ~ ., data = select(treino, am, wt, qsec),
kernel = "polynomial", cost = 1,
gamma=0.3, coef0=0.1, degree=3, scale = T)
svmfit.p
##
## Call:
## svm(formula = am ~ ., data = select(treino, am, wt, qsec), kernel = "polynomial", cost = 1, gamma = 0.3,
## coef0 = 0.1, degree = 3, scale = T)
##
##
## Parameters:
## SVM-Type: C-classification
## SVM-Kernel: polynomial
## cost: 1
## degree: 3
## coef.0: 0.1
##
## Number of Support Vectors: 19
Note que com o kernel polinomial utilizamos mais parâmetros. São eles gamma, coef0 e degree. Naquela fórmula explicada mais acima ( $K(x,y) = [\gamma(x^{T}y) + r]^{d}$ ), esses parâmetros são respectivamente $\gamma$, $r$ e $d$.
plot( svmfit.p, select(treino, am, wt, qsec),
col=c("cornflowerblue", "darkred"))
Da mesma forma, podemos usar a função tune para testar mais de um valor em cada parâmetro.
set.seed(59)
tunefit.p = tune(svm, am ~ ., data = select(treino, am, qsec, wt),
kernel = "polynomial",
ranges = list(cost = c(0.001, 0.01, 0.1, 1, 5, 10, 50),
gamma = c(0.5, 1, 2, 3, 4),
coef0 = c(0, 0.1, 0.5, 1),
degree = c(1, 2, 3)))
tunefit.p$best.model
##
## Call:
## best.tune(method = svm, train.x = am ~ ., data = select(treino, am, qsec, wt), ranges = list(cost = c(0.001,
## 0.01, 0.1, 1, 5, 10, 50), gamma = c(0.5, 1, 2, 3, 4), coef0 = c(0, 0.1, 0.5, 1), degree = c(1,
## 2, 3)), kernel = "polynomial")
##
##
## Parameters:
## SVM-Type: C-classification
## SVM-Kernel: polynomial
## cost: 50
## degree: 3
## coef.0: 0.5
##
## Number of Support Vectors: 7
Com isso, podemos avaliar o modelo
# realizando a predicao sob o conjunto de teste
predicao = predict(tunefit.p$best.model, select(teste, am, wt, qsec))
# obtendo a matriz de confusao
confusionMatrix(data = predicao, reference = teste$am)
## Confusion Matrix and Statistics
##
## Reference
## Prediction automatic manual
## automatic 5 0
## manual 0 3
##
## Accuracy : 1
## 95% CI : (0.6306, 1)
## No Information Rate : 0.625
## P-Value [Acc > NIR] : 0.02328
##
## Kappa : 1
##
## Mcnemar's Test P-Value : NA
##
## Sensitivity : 1.000
## Specificity : 1.000
## Pos Pred Value : 1.000
## Neg Pred Value : 1.000
## Prevalence : 0.625
## Detection Rate : 0.625
## Detection Prevalence : 0.625
## Balanced Accuracy : 1.000
##
## 'Positive' Class : automatic
##
# outra forma de obter a precisao
mean(predicao == teste$am)
## [1] 1
Utilizando Kernel radial
Observe agora a distribuição das variáveis mpg e qsec
Vamos treinar um modelo com kernel radial utilizando elas
set.seed(751)
svmfit.r = svm(am ~ ., data = select(treino, am, mpg, qsec),
kernel = "radial", gamma=0.5, cost = 10, scale = T)
svmfit.r
##
## Call:
## svm(formula = am ~ ., data = select(treino, am, mpg, qsec), kernel = "radial", gamma = 0.5, cost = 10,
## scale = T)
##
##
## Parameters:
## SVM-Type: C-classification
## SVM-Kernel: radial
## cost: 10
##
## Number of Support Vectors: 10
plot(svmfit.r, select(treino, am, qsec, mpg),
col=c("cornflowerblue", "darkred"))
Para o modelo com kernel radial, precisamos informar apenas o parâmetro gamma (O mesmo $\gamma$ da fórmula $K(x,y) = e^{-\gamma |
x-y | ^{2}}$ ). Vamos testar com outros valores de parâmetros |
set.seed(751)
tunefit.r = tune(svm, am ~ ., data = select(treino, am, qsec, mpg),
kernel = "radial",
ranges = list(cost = c(0.001, 0.01, 0.1, 1, 5, 10, 100),
gamma = c(0.5,1,2,3,4)))
tunefit.r$best.model
##
## Call:
## best.tune(method = svm, train.x = am ~ ., data = select(treino, am, qsec, mpg), ranges = list(cost = c(0.001,
## 0.01, 0.1, 1, 5, 10, 100), gamma = c(0.5, 1, 2, 3, 4)), kernel = "radial")
##
##
## Parameters:
## SVM-Type: C-classification
## SVM-Kernel: radial
## cost: 10
##
## Number of Support Vectors: 13
e avaliando,
# realizando a predicao sob o conjunto de teste
predicao = predict(tunefit.r$best.model, select(teste, am, mpg, qsec))
# obtendo a matriz de confusao
confusionMatrix(data = predicao, reference = teste$am)
## Confusion Matrix and Statistics
##
## Reference
## Prediction automatic manual
## automatic 5 0
## manual 0 3
##
## Accuracy : 1
## 95% CI : (0.6306, 1)
## No Information Rate : 0.625
## P-Value [Acc > NIR] : 0.02328
##
## Kappa : 1
##
## Mcnemar's Test P-Value : NA
##
## Sensitivity : 1.000
## Specificity : 1.000
## Pos Pred Value : 1.000
## Neg Pred Value : 1.000
## Prevalence : 0.625
## Detection Rate : 0.625
## Detection Prevalence : 0.625
## Balanced Accuracy : 1.000
##
## 'Positive' Class : automatic
##
# outra forma de obter a precisao
mean(predicao == teste$am)
## [1] 1
SVM com a função ksvm() do pacote kernlab
Novamente, vamos trabalhar com a base mtcars.
data("mtcars")
mtcars$am = factor(mtcars$am, labels = c("automatic","manual"))
set.seed(95)
noTreino = caret::createDataPartition(y = mtcars$am, p = 0.7, list = F)
treino = mtcars[noTreino,]
teste = mtcars[-noTreino,]
Utilizando Kernel linear
library(ggplot2)
ggplot(data = treino, aes(x = hp, y = wt, color = am)) +
geom_point(size = 3) +
scale_color_manual(values=c("darkolivegreen3", "brown2")) +
theme_minimal()
Também podemos criar modelos de SVM utilizando a função ksvm presente no pacote
library(kernlab)
kernfit.l = ksvm(am ~ ., data = select(mtcars, am, wt, hp),
type = "C-svc", kernel = 'vanilladot', C=1)
## Setting default kernel parameters
Os principais argumentos dessa função são:
- type = Precisa ser informado. Indica qual é o tipo de preditor que queremos criar. Para classificadores, podemos usar ‘C-svc’. Para regressores, podemos usar ‘eps-svr’. Para outros types, veja a documentação da função no Help do RStudio ou neste link.
- kernel = Indica o tipo de kernel. Vamos explorar o ‘vanilladot’ para linear, ‘polydot’ para polinomial e ‘rbfdot’ para radial (default), mas existem outros.
- C = Quantifica a penalidade associada a uma predição incorreta. Default=1.
- scaled = Se TRUE (default), padroniza as variáveis.
- kpar = Lista os parâmetros necessários para o kernel utilizado. Seu default é automatico, ou seja, ele encontra o(s) parâmetros que melhor ajustam o modelo automaticamente. Mas podemos alterar se quisermos.
- kernel linear -> não possui parâmetros
- kernel polinomial -> Utiliza os parâmetros
degree,scaleeoffset. - kernel radial -> Utiliza o parâmetro
sigma.
kernfit.l
## Support Vector Machine object of class "ksvm"
##
## SV type: C-svc (classification)
## parameter : cost C = 1
##
## Linear (vanilla) kernel function.
##
## Number of Support Vectors : 14
##
## Objective Function Value : -8.9358
## Training error : 0.0625
# obtendo a precisão dentro da amostra
1 - kernfit.l@error
## [1] 0.9375
#plot(kernfit.l, data = select(treino, am, wt, hp))
E podemos avaliar, obtendo a precisão fora da amostra
# realizando a predicao sob o conjunto de teste
predicao = kernfit.l %>% predict(select(teste, am, wt, hp))
# obtendo a matriz de confusao
caret::confusionMatrix(data = predicao, reference = teste$am)
## Confusion Matrix and Statistics
##
## Reference
## Prediction automatic manual
## automatic 4 0
## manual 1 3
##
## Accuracy : 0.875
## 95% CI : (0.4735, 0.9968)
## No Information Rate : 0.625
## P-Value [Acc > NIR] : 0.135
##
## Kappa : 0.75
##
## Mcnemar's Test P-Value : 1.000
##
## Sensitivity : 0.800
## Specificity : 1.000
## Pos Pred Value : 1.000
## Neg Pred Value : 0.750
## Prevalence : 0.625
## Detection Rate : 0.500
## Detection Prevalence : 0.500
## Balanced Accuracy : 0.900
##
## 'Positive' Class : automatic
##
# outra forma de obter a precisao
mean(predicao == teste$am)
## [1] 0.875
Utilizando Kernel polinomial
Para treinar um modelo svm com kernel polinomial, usamos o argumento ‘kernel=’polydot’’ e passamos a lista de parametros necessários (degree, offset e scale).
set.seed(284)
kernfit.p = ksvm(am ~ ., data = select(treino, am, qsec, wt),
type = "C-svc", kernel = 'polydot',
C=1, kpar=list(degree=3, offset=0.1))
kernfit.p
## Support Vector Machine object of class "ksvm"
##
## SV type: C-svc (classification)
## parameter : cost C = 1
##
## Polynomial kernel function.
## Hyperparameters : degree = 3 scale = 1 offset = 0.1
##
## Number of Support Vectors : 9
##
## Objective Function Value : -5.3132
## Training error : 0.083333
plot(kernfit.p, data = select(treino, am, qsec, wt))
a avaliação é feita da mesma forma que as anteriores: As observações marcadas com um triângulo são as rotuladas com câmbio automático, enquanto as marcadas com círculo são as de câmbio manual. As formas preenchidas são as que foram usadas como vetor de suporte. Finalmente, a região azulada é onde as novas observações presentes ali serão classificadas com câmbio manual, enquanto na região avermelhada, serão classificadas automático
Utilizando Kernel radial
No caso radial, usamos ‘kernel=’rdfdot’’ e passamos o valor sigma.
set.seed(614)
kernfit.r = ksvm(am ~ ., data = select(treino, am, qsec, mpg),
type = "C-svc", kernel = 'rbfdot',
C=10, kpar=list(sigma=0.5))
kernfit.r
## Support Vector Machine object of class "ksvm"
##
## SV type: C-svc (classification)
## parameter : cost C = 10
##
## Gaussian Radial Basis kernel function.
## Hyperparameter : sigma = 0.5
##
## Number of Support Vectors : 11
##
## Objective Function Value : -34.0858
## Training error : 0
plot(kernfit.r, data = select(treino, am, qsec, mpg))
SVM com a função train() do pacote caret
Ainda usando a base mtcars, vamos ver como utilizar a função train do caret para treinar um modelo de SVM. Os principais argumentos dessa função são:
- method = Para SVM com kernel linear, ele recebe ‘svmLinear’. Para polinomial, ‘svmPoly’. E para radial, ‘svmRadial’.
- tuneGrid ou tuneLength = usando para testar alguns valores dos parâmetros usados. (Vamos entender melhor usando)
Utilizando Kernel linear
library(caret); library(dplyr)
# treinando o modelo
set.seed(24)
modelfit.l = caret::train(am ~ ., data = select(treino, am, wt, qsec),
method="svmLinear", preProcess = c("center","scale"),
tuneGrid = expand.grid(C = seq(0, 2, length = 15) ) )
O kernel linear não possui parâmetros, portanto só precisamos passar o custo aqui representado por C. Usando tuneGrid = expand.grid() podemos passar um ou mais valores para cada parâmetro da função e para o C e ele testa todos eles e decide qual é o melhor.
modelfit.l
## Support Vector Machines with Linear Kernel
##
## 24 samples
## 2 predictor
## 2 classes: 'automatic', 'manual'
##
## Pre-processing: centered (2), scaled (2)
## Resampling: Bootstrapped (25 reps)
## Summary of sample sizes: 24, 24, 24, 24, 24, 24, ...
## Resampling results across tuning parameters:
##
## C Accuracy Kappa
## 0.0000000 NaN NaN
## 0.1428571 0.8339278 0.6074720
## 0.2857143 0.8844228 0.6865752
## 0.4285714 0.8735036 0.6672053
## 0.5714286 0.8829481 0.6874628
## 0.7142857 0.8869481 0.6955080
## 0.8571429 0.8847258 0.6923804
## 1.0000000 0.8883622 0.6996517
## 1.1428571 0.8883622 0.6996517
## 1.2857143 0.8883622 0.6996517
## 1.4285714 0.9053622 0.7343507
## 1.5714286 0.9053622 0.7343507
## 1.7142857 0.9093622 0.7414732
## 1.8571429 0.9093622 0.7669594
## 2.0000000 0.9128066 0.7704828
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was C = 2.
Aqui, ele testou 15 valores para C e concluiu que a melhor precisão ocorria quando C = 2.
plot(modelfit.l)
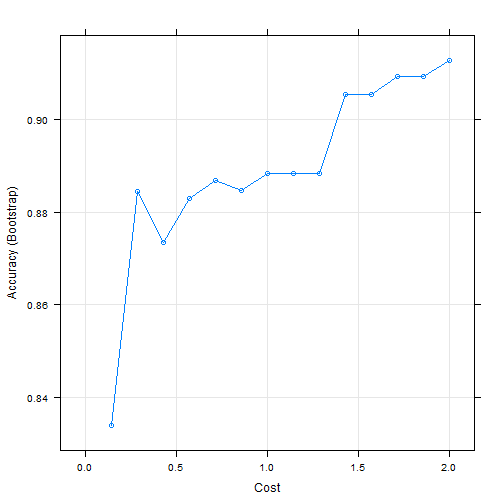
Aqui podemos observar a distribuição da precisão para cada valor de custo que testamos.
Utilizando Kernel polinomial
set.seed(882)
modelfit.p = caret::train(am ~ ., data = select(treino, am, qsec, wt),
method="svmPoly", tuneLength = 4,
preProcess = c("center","scale"))
Para o kernel polinomial, os parâmetros são degree e scale além do C.
Usando o tuneLength, podemos passar uma quantidade n e ele testará todas as combinação com os n primeiros valores default de cada parâmetro.
modelfit.p
## Support Vector Machines with Polynomial Kernel
##
## 24 samples
## 2 predictor
## 2 classes: 'automatic', 'manual'
##
## Pre-processing: centered (2), scaled (2)
## Resampling: Bootstrapped (25 reps)
## Summary of sample sizes: 24, 24, 24, 24, 24, 24, ...
## Resampling results across tuning parameters:
##
## degree scale C Accuracy Kappa
## 1 0.001 0.25 0.5161659 0.1189539
## 1 0.001 0.50 0.5161659 0.1189539
## 1 0.001 1.00 0.5161659 0.1189539
## 1 0.001 2.00 0.5161659 0.1189539
## 1 0.010 0.25 0.5161659 0.1189539
## 1 0.010 0.50 0.5161659 0.1189539
## 1 0.010 1.00 0.5161659 0.1189539
## 1 0.010 2.00 0.5161659 0.1189539
## 1 0.100 0.25 0.5436912 0.1793538
## 1 0.100 0.50 0.6534387 0.3891840
## 1 0.100 1.00 0.8405094 0.7183571
## 1 0.100 2.00 0.8765743 0.7878575
## 1 1.000 0.25 0.8998470 0.8091447
## 1 1.000 0.50 0.9273925 0.8454360
## 1 1.000 1.00 0.9507431 0.8910997
## 1 1.000 2.00 0.9551876 0.9020088
## 2 0.001 0.25 0.5161659 0.1189539
## 2 0.001 0.50 0.5161659 0.1189539
## 2 0.001 1.00 0.5161659 0.1189539
## 2 0.001 2.00 0.5161659 0.1189539
## 2 0.010 0.25 0.5161659 0.1189539
## 2 0.010 0.50 0.5161659 0.1189539
## 2 0.010 1.00 0.5161659 0.1189539
## 2 0.010 2.00 0.6264704 0.3271633
## 2 0.100 0.25 0.6846782 0.4521554
## 2 0.100 0.50 0.8412237 0.7195571
## 2 0.100 1.00 0.8765743 0.7828179
## 2 0.100 2.00 0.9237561 0.8417467
## 2 1.000 0.25 0.9058167 0.7886891
## 2 1.000 0.50 0.9198817 0.8181146
## 2 1.000 1.00 0.9227258 0.8284860
## 2 1.000 2.00 0.9227258 0.8255929
## 3 0.001 0.25 0.5161659 0.1189539
## 3 0.001 0.50 0.5161659 0.1189539
## 3 0.001 1.00 0.5161659 0.1189539
## 3 0.001 2.00 0.5161659 0.1189539
## 3 0.010 0.25 0.5161659 0.1189539
## 3 0.010 0.50 0.5161659 0.1189539
## 3 0.010 1.00 0.5586912 0.2125406
## 3 0.010 2.00 0.7107734 0.4831787
## 3 0.100 0.25 0.8275570 0.6946523
## 3 0.100 0.50 0.8592237 0.7463197
## 3 0.100 1.00 0.8954055 0.8078916
## 3 0.100 2.00 0.9294704 0.8464987
## 3 1.000 0.25 0.8975195 0.7884825
## 3 1.000 0.50 0.9196003 0.8289326
## 3 1.000 1.00 0.9236003 0.8343143
## 3 1.000 2.00 0.9336003 0.8529297
##
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were degree = 1, scale = 1 and C = 2.
modelfit.p$bestTune
## degree scale C
## 16 1 1 2
e então ele utiliza a combinação que possui a melhor precisão.
plot(modelfit.p)
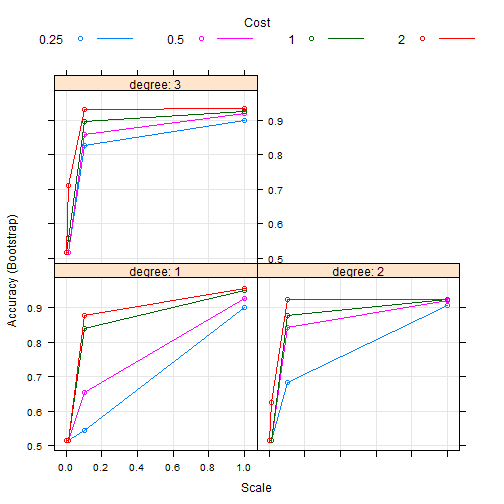
O plot nos mostra a distribuição da precisão em cada combinação de custo, degree e scale. Por exemplo, podemos ver que usando $degree=1$ (Primeiro quadro), $scale=0.1$ (eixo x/abscissa) e $C=2$ (linha vermelha) alcançamos uma precisão em torno de $0.88$ (eixo y/ordenadas).
Avaliando o modelo:
predicao = modelfit.p %>% predict( select(teste, am, qsec, wt) )
# obtendo a matriz de confusao
confusionMatrix(data = predicao, reference = teste$am)
## Confusion Matrix and Statistics
##
## Reference
## Prediction automatic manual
## automatic 4 0
## manual 1 3
##
## Accuracy : 0.875
## 95% CI : (0.4735, 0.9968)
## No Information Rate : 0.625
## P-Value [Acc > NIR] : 0.135
##
## Kappa : 0.75
##
## Mcnemar's Test P-Value : 1.000
##
## Sensitivity : 0.800
## Specificity : 1.000
## Pos Pred Value : 1.000
## Neg Pred Value : 0.750
## Prevalence : 0.625
## Detection Rate : 0.500
## Detection Prevalence : 0.500
## Balanced Accuracy : 0.900
##
## 'Positive' Class : automatic
##
# outra forma de obter a precisao
mean(predicao == teste$am)
## [1] 0.875
Utilizando Kernel radial
set.seed(109)
modelfit.r = caret::train(am ~ ., data = select(treino, am, qsec, mpg),
method = "svmRadial", preProcess = c("center","scale"),
tuneGrid=expand.grid(C=c(0.5,1,5,10),
sigma=seq(0.5,1.5, length=5)))
Para o kernel radial, temos o parâmetro sigma.
modelfit.r
## Support Vector Machines with Radial Basis Function Kernel
##
## 24 samples
## 2 predictor
## 2 classes: 'automatic', 'manual'
##
## Pre-processing: centered (2), scaled (2)
## Resampling: Bootstrapped (25 reps)
## Summary of sample sizes: 24, 24, 24, 24, 24, 24, ...
## Resampling results across tuning parameters:
##
## C sigma Accuracy Kappa
## 0.5 0.50 0.7916118 0.5710319
## 0.5 0.75 0.7870693 0.5735315
## 0.5 1.00 0.7660996 0.5332282
## 0.5 1.25 0.7629076 0.5247248
## 0.5 1.50 0.7433045 0.4873416
## 1.0 0.50 0.7769913 0.5500594
## 1.0 0.75 0.7529105 0.5013235
## 1.0 1.00 0.7524488 0.5055922
## 1.0 1.25 0.7430981 0.4930791
## 1.0 1.50 0.7380981 0.4816286
## 5.0 0.50 0.7794156 0.5438133
## 5.0 0.75 0.7563377 0.5038143
## 5.0 1.00 0.7420346 0.4818703
## 5.0 1.25 0.7460346 0.4960802
## 5.0 1.50 0.7308759 0.4725168
## 10.0 0.50 0.7890188 0.5662949
## 10.0 0.75 0.7762107 0.5495060
## 10.0 1.00 0.7584156 0.5178123
## 10.0 1.25 0.7517489 0.5119656
## 10.0 1.50 0.7251616 0.4630399
##
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were sigma = 0.5 and C = 0.5.
plot(modelfit.r)
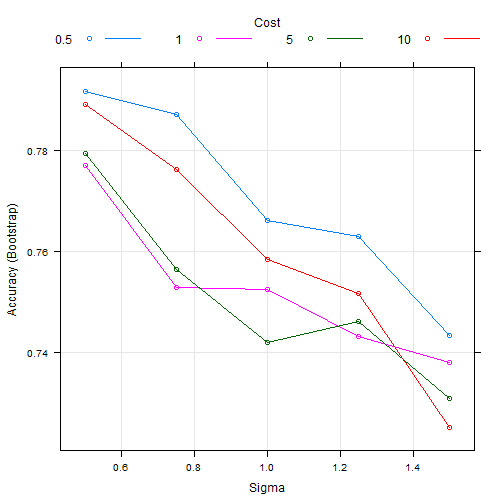
Podemos ver aqui um resumo dos argumentos equivalentes em cada função e seus valores default. A primeira nomeclatura é referente as fórmulas apresentadas.
| Argumento | e1071::svm | kernlab::ksvm | caret::train | Observações |
|---|---|---|---|---|
| Custo | cost = 1 |
C = 1 |
C |
Quantifica a penalidade associada a uma predição incorreta. |
| Kernel linear | ‘linear’ | ‘vanilladot’ | ‘svmLinear’ | Não necessita de parâmetros. |
| Kernel polinomial | ‘polynomial’ | ‘polydot’ | ‘svmPoly’ | Utiliza os parâmetros $\gamma$, $r$ e $degree$. |
| Kernel radial | ‘radial’ | ‘rdfdot’ | ‘svmRadial’ | Utiliza o parâmetro $\gamma$. |
| $\gamma$ | gamma = $\frac{1}{nº colunas\ da\ base}$ |
scale se o kernel for polinomial. sigma se o kernel for radial. |
scale se o kernel for polinomial. sigma se o kernel for radial. |
Escala a quantidade de influência que duas observações têm uma sobre a outra. |
| $r$ | coef0 = 0 |
offset |
Determina o coeficiente do polinômio. | |
| $d$ | degree = 3 |
degree = 1 |
degree |
Determina p grau do polinômio. |
| Padronizar | scale = T |
scaled = T |
preProcess = c("center","scale") |
Padroniza as variáveis deixando todas na mesma escala. |
K-Nearest Neighbors (KNN)
O método K-Nearest Neighbors (KNN) - K vizinhos mais próximos - já foi brevemente comentado neste material no capítulo de pré-processamento, com o objetivo de tratar NA’s em uma base de dados. Agora veremos como utilizá-lo para problemas de machine learning de classificação e regressão. Veremos os detalhes de como o método funciona para ambos os casos e duas formas de implementá-lo: utilizando funções do pacote FNN e a função train() do pacote caret.
Em Classificação
O método KNN assume que há similaridade em observações próximas do conjunto de dados. A previsão para uma nova amostra é feita pesquisando em todo o conjunto de treinamento os k vizinhos mais próximos dessa amostra, e assim computando a classe mais observada (moda) à essa observação. Ou seja, diferentemente dos outros métodos vistos até agora, o KNN é um modelo que não precisa ser treinado.
Outros pontos que são importantes ser citados são:
1 - O KNN é mais adequado para dados de baixa dimensão (poucas variáveis), e
2 - O KNN é considerado um algoritmo “preguiçoso” (lento).
Vamos entender o passo a passo de como o método funciona a seguir. Considere que a amostra abaixo seja nossa amostra treino.
treino = readxl::read_excel("heart_treino.xlsx")
treino
## # A tibble: 7 x 3
## RestBP Chol AHD
## <dbl> <dbl> <chr>
## 1 145 233 No
## 2 160 286 Yes
## 3 130 250 No
## 4 120 236 No
## 5 120 354 No
## 6 130 254 Yes
## 7 140 203 Yes
Queremos predizer se uma pessoa possui uma doença cardíaca (variável “AHD”) baseado nas seguintes variáveis:
- RestBP: pressão arterial, medida em milímetros de mercúrio (mmHg);
- Chol: colesterol sérico, medido em miligramas por decilitro (mg/dl).
Como não precisamos treinar o modelo, vamos carregar a amostra teste para aplicá-lo.
teste = readxl::read_excel("heart_teste.xlsx")
teste
## # A tibble: 3 x 3
## RestBP Chol AHD
## <dbl> <dbl> <chr>
## 1 120 229 Yes
## 2 130 204 No
## 3 140 268 Yes
Como a amostra teste serve para simular uma nova amostra, precisamos utilizá-la sem os rótulos na variável a ser predita. Assim, vamos criar uma nova amostra teste não rotulada.
teste_predicao = teste
# Retirando os rótulos:
teste_predicao$AHD = NA
# Juntando em uma mesma base para facilitar as contas e a plotagem do gráfico:
base = rbind(treino, teste_predicao)
# Inserindo uma nova coluna com a numeração das observações:
base = tibble::add_column(base, X1 = 1:10, .before = "RestBP")
# Gráfico:
library(ggplot2)
ggplot(base, aes(x = RestBP, y = Chol, color = AHD)) + geom_point(size = 3) + theme_minimal() +
geom_text(aes(label = X1), vjust = 1, hjust = 1) + xlab("Pressão Arterial (mmHg)") +
ylab("Colesterol Sérico (mg/dl)") + ggtitle("Presença de Doença Cardíaca em Pacientes") +
scale_colour_discrete(name = "Doença Cardíaca", breaks = c("No", "Yes", NA),
labels = c("Não", "Sim", "Desconhecido"))
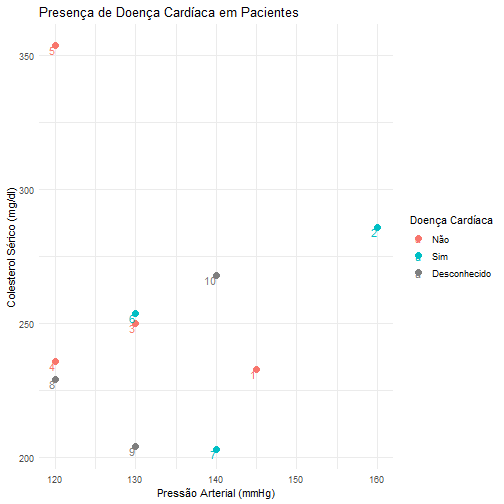
O primeiro passo é escolher um valor para o k. Como a predição será feita com base na moda das k classificações mais próximas da amostra, é recomendado escolher um k ímpar, para evitar algum possível empate. Vamos utilizar k = 3.
OBS: o melhor valor para k pode ser encontrado por cross validation.
Para verificar quais são os 3 vizinhos mais próximos das observações precisamos calcular as distâncias entre elas e todas as observações do conjunto de dados e pegar as 3 menores. Existem vários métodos de se calcular a distância entre dois pontos, mas a mais usual é a distância euclidiana.
Distância Euclidiana:
Sejam $p = (p_1, p_2, …, p_n)$ e $q = (q_1, q_2, …, q_n)$ dois pontos de dimensão n. A distância euclidiana entre p e q é definida como: \(\operatorname{d}(p,q) = \sqrt{\sum\limits_{i=1}^{n} (p_i-q_i)^{2}}.\)
Vamos, primeiramente, calcular a distância euclidiana entra a observação 8 (a primeira do conjunto teste) e todas as demais observações.
## # A tibble: 10 x 4
## X1 RestBP Chol AHD
## <int> <dbl> <dbl> <chr>
## 1 1 145 233 No
## 2 2 160 286 Yes
## 3 3 130 250 No
## 4 4 120 236 No
## 5 5 120 354 No
## 6 6 130 254 Yes
## 7 7 140 203 Yes
## 8 8 120 229 <NA>
## 9 9 130 204 <NA>
## 10 10 140 268 <NA>
- Distância entre as observações 8 e 1: $\sqrt{(120-145)^{2}+(229-233)^{2}} = 25,318$;
- Distância entre as observações 8 e 2: $\sqrt{(120-160)^{2}+(229-286)^{2}} = 69,635$;
- Distância entre as observações 8 e 3: $\sqrt{(120-130)^{2}+(229-250)^{2}} = 23,259$;
- Distância entre as observações 8 e 4: $\sqrt{(120-120)^{2}+(229-236)^{2}} = 7,000$;
- Distância entre as observações 8 e 5: $\sqrt{(120-120)^{2}+(229-354)^{2}} = 125,000$;
- Distância entre as observações 8 e 6: $\sqrt{(120-130)^{2}+(229-254)^{2}} = 26,926$;
- Distância entre as observações 8 e 7: $\sqrt{(120-140)^{2}+(229-203)^{2}} = 32,802$.
Podemos ver que as observações mais próximas da observação 8 são as observações 4, 3 e 1, respectivamente.
ggplot(base, aes(x = RestBP, y = Chol, color = AHD)) + geom_point(size = 3) +
theme_minimal() + geom_text(aes(label = X1), vjust = 1, hjust = 1) +
xlab("Pressão Arterial (mmHg)") + ylab("Colesterol Sérico (mg/dl)") +
ggtitle("Presença de Doença Cardíaca em Pacientes") +
geom_segment(aes(x = 120, xend = 120, y = 229, yend = 236), size = .8, color = "black") +
geom_segment(aes(x = 120, xend = 130, y = 229, yend = 250), size = .8, color = "black") +
geom_segment(aes(x = 120, xend = 145, y = 229, yend = 233), size = .8, color = "black") +
scale_colour_discrete(name = "Doença Cardíaca", breaks = c("No", "Yes", NA),
labels = c("Não", "Sim", "Desconhecido"))
Logo, como as 3 observações são classificadas como “Não” para a variável de interesse, imputamos essa classificação à observação que queremos prever.
# Convertendo a coluna com as predições para character para poder acrescentar a predição:
teste_predicao$AHD = as.character(teste_predicao$AHD)
# A observação 8 na "base" é a observação 1 no "teste_predicao".
teste_predicao[1,3] = "No"
teste_predicao
## # A tibble: 3 x 3
## RestBP Chol AHD
## <dbl> <dbl> <chr>
## 1 120 229 No
## 2 130 204 <NA>
## 3 140 268 <NA>
Agora vamos realizar o mesmo procedimento para a observação 9:
## # A tibble: 10 x 4
## X1 RestBP Chol AHD
## <int> <dbl> <dbl> <chr>
## 1 1 145 233 No
## 2 2 160 286 Yes
## 3 3 130 250 No
## 4 4 120 236 No
## 5 5 120 354 No
## 6 6 130 254 Yes
## 7 7 140 203 Yes
## 8 8 120 229 <NA>
## 9 9 130 204 <NA>
## 10 10 140 268 <NA>
- Distância entre as observações 9 e 1: $\sqrt{(130-145)^{2}+(204-233)^{2}} = 32,650$;
- Distância entre as observações 9 e 2: $\sqrt{(130-160)^{2}+(204-286)^{2}} = 87,316$;
- Distância entre as observações 9 e 3: $\sqrt{(130-130)^{2}+(204-250)^{2}} = 46,000$;
- Distância entre as observações 9 e 4: $\sqrt{(130-120)^{2}+(204-236)^{2}} = 33,526$;
- Distância entre as observações 9 e 5: $\sqrt{(130-120)^{2}+(204-354)^{2}} = 150,333$;
- Distância entre as observações 9 e 6: $\sqrt{(130-130)^{2}+(204-254)^{2}} = 50,000$;
- Distância entre as observações 9 e 7: $\sqrt{(130-140)^{2}+(204-203)^{2}} = 10,050$.
Podemos notar que as observações mais próximas das observações 9 são as observações 7, 1 e 4.
ggplot(base, aes(x = RestBP, y = Chol, color = AHD)) + geom_point(size = 3) +
theme_minimal() + geom_text(aes(label = X1), vjust = 1, hjust = 1) +
xlab("Pressão Arterial (mmHg)") + ylab("Colesterol Sérico (mg/dl)") +
ggtitle("Presença de Doença Cardíaca em Pacientes") +
geom_segment(aes(x = 130, xend = 140, y = 204, yend = 203), size = .8, color = "black") +
geom_segment(aes(x = 130, xend = 145, y = 204, yend = 233), size = .8, color = "black") +
geom_segment(aes(x = 130, xend = 120, y = 204, yend = 236), size = .8, color = "black") +
scale_colour_discrete(name = "Doença Cardíaca", breaks = c("No", "Yes", NA),
labels = c("Não", "Sim", "Desconhecido"))
Como 2 das 3 observações são classificadas como “Não”, a observação 9 recebe a classificação “Não”.
# A observação 9 na "base" é a observação 2 no "teste_predicao".
teste_predicao[2,3] = "No"
teste_predicao
## # A tibble: 3 x 3
## RestBP Chol AHD
## <dbl> <dbl> <chr>
## 1 120 229 No
## 2 130 204 No
## 3 140 268 <NA>
Por último, vamos classificar a observação 10.
## # A tibble: 10 x 4
## X1 RestBP Chol AHD
## <int> <dbl> <dbl> <chr>
## 1 1 145 233 No
## 2 2 160 286 Yes
## 3 3 130 250 No
## 4 4 120 236 No
## 5 5 120 354 No
## 6 6 130 254 Yes
## 7 7 140 203 Yes
## 8 8 120 229 <NA>
## 9 9 130 204 <NA>
## 10 10 140 268 <NA>
- Distância entre as observações 10 e 1: $\sqrt{(140-145)^{2}+(268-233)^{2}} = 35,355$;
- Distância entre as observações 10 e 2: $\sqrt{(140-160)^{2}+(268-286)^{2}} = 26,907$;
- Distância entre as observações 10 e 3: $\sqrt{(140-130)^{2}+(268-250)^{2}} = 20,591$;
- Distância entre as observações 10 e 4: $\sqrt{(140-120)^{2}+(268-236)^{2}} = 37,736$;
- Distância entre as observações 10 e 5: $\sqrt{(140-120)^{2}+(268-354)^{2}} = 88,295$;
- Distância entre as observações 10 e 6: $\sqrt{(140-130)^{2}+(268-254)^{2}} = 17,205$;
- Distância entre as observações 10 e 7: $\sqrt{(140-140)^{2}+(268-203)^{2}} = 65,000$.
Assim, as observações mais próximas da observação 10 são as observações 6, 3 e 2.
ggplot(base, aes(x = RestBP, y = Chol, color = AHD)) + geom_point(size = 3) +
theme_minimal() + geom_text(aes(label = X1), vjust = 1, hjust = 1) +
xlab("Pressão Arterial (mmHg)") + ylab("Colesterol Sérico (mg/dl)") +
ggtitle("Presença de Doença Cardíaca em Pacientes") +
geom_segment(aes(x = 140, xend = 130, y = 268, yend = 254), size = .8, color = "black") +
geom_segment(aes(x = 140, xend = 130, y = 268, yend = 250), size = .8, color = "black") +
geom_segment(aes(x = 140, xend = 160, y = 268, yend = 286), size = .8, color = "black") +
scale_colour_discrete(name = "Doença Cardíaca", breaks = c("No", "Yes", NA),
labels = c("Não", "Sim", "Desconhecido"))
Então a observação recebe a classificação “Sim”, visto que 2 das 3 observações mais próximas à ela são classificadas como “Sim”.
# A observação 10 na "base" é a observação 3 no "teste_predicao".
teste_predicao[3,3] = "Yes"
teste_predicao
## # A tibble: 3 x 3
## RestBP Chol AHD
## <dbl> <dbl> <chr>
## 1 120 229 No
## 2 130 204 No
## 3 140 268 Yes
E assim terminamos as nossas predições. Vamos construir a matriz de confusão para ver o quanto acertamos:
table(teste_predicao$AHD, teste$AHD)
##
## No Yes
## No 1 1
## Yes 0 1
O algoritmo acertou 2 das 3 classificações da amostra teste, o que nos dá uma precisão de 66,67%, uma sensibilidade de 50% e uma especificidade de 100%. Como identificar os pacientes que possuem uma doença cardíaca é mais importante do que identificar os que não possuem, devemos dar mais peso à sensibilidade do nosso modelo do que à especificidade. Ou seja, o modelo não se saiu tão bem quanto o esperado, mas isso se deve principalmente ao fato de termos utilizado uma amostra muito pequena. Se obtivéssemos essas medidas num problema real (com bases grandes), esse modelo não seria o mais adequado. Outro fator que deve ser levado em conta também é a escolha do valor de k, que não deve ser feita de forma aleatória e sim de forma a otimizar o modelo.
Em Regressão
Para esse exemplo, vamos utilizar a base de dados faithful do pacote básico do R. Queremos prever o tempo de espera (waiting) entre uma erupção e outra de um geiser dado o tempo de erupção (eruption).
data("faithful")
library(caret)
set.seed(100)
noTreino = createDataPartition(faithful$waiting, p=0.7, list=F)
treino = faithful[noTreino,]
teste = faithful[-noTreino,]
ggplot(treino, aes(x=eruptions, y=waiting)) +
geom_point() + theme_minimal()
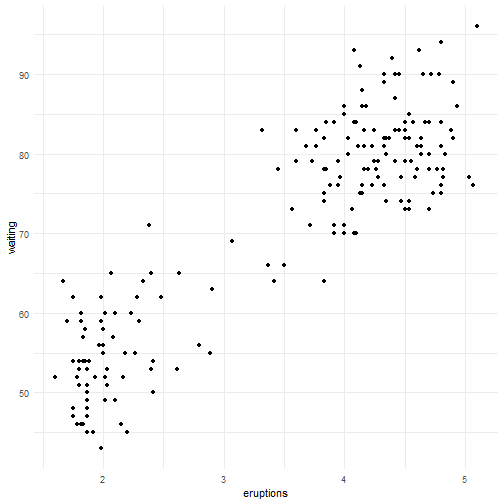
Suponha que obtivemos uma nova observação cujo tempo de erupção foi de $3.2$, indicado pela linha vermelha.
ggplot(treino, aes(x=eruptions, y=waiting)) +
geom_point() + theme_minimal() +
geom_vline(xintercept= 3.2, colour="red")
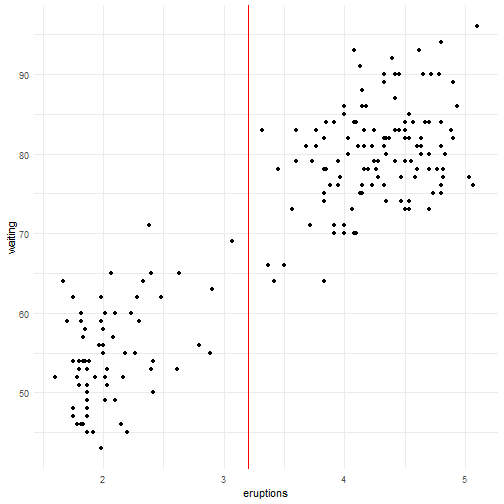
Assim como em classificação, a ideia do KNN é estimar o valor pela média das sobservações menos distantes. Essa distância pode ser obtida pela método Euclidiano, de Manhattan ou ainda outro. O mais comum é o Euclidiano ($\operatorname{d}(p,q) = \sqrt{\sum\limits_{i=1}^{n} (p_i-q_i)^{2}}$) que é o que usaremos.
# calculando a distancia euclidiana
treino= mutate(treino,
distancia = sqrt( (eruptions - 3.2)^2 ) )
# mostrando a primeira observação da base ordenada pela distancia
head(arrange(treino, distancia), n=1)
## eruptions waiting distancia
## 1 3.317 83 0.117
O vizinho mais próximo de $3.2$ é $3.317$. Então, usando um k=1, temos que o tempo estimado de espera (waiting) para essa nova observação é a média dos valores vizinhos. Nesse caso, $83$ indicado pelo ponto vermelho.
(media = mean(head(arrange(treino, distancia), n=1)$waiting))
## [1] 83
# k = 1
ggplot(treino, aes(x=eruptions, y=waiting)) +
geom_point() + theme_minimal() +
annotate("rect", xmin = (3.2 - 0.12), xmax = (3.2 + 0.12),
ymin = 40, ymax = 100, alpha = 0.2, fill = "red") +
annotate("pointrange", x = 3.2, y = media,
ymin = 40, ymax = 100, colour = "red",
size = .5, alpha=0.5)
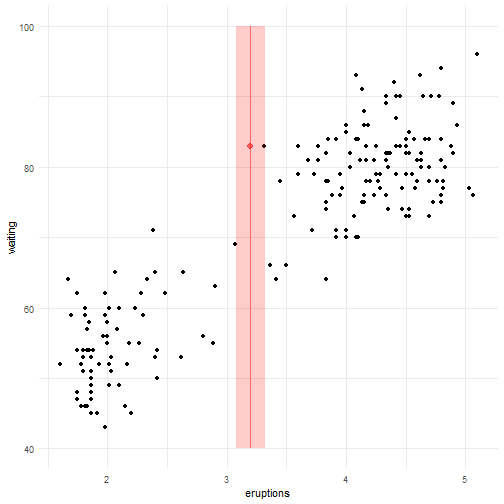
Poderiamos usar um k=10, nesse caso, teriamos
head(arrange(treino, distancia), n=10)
## eruptions waiting distancia
## 1 3.317 83 0.117
## 2 3.067 69 0.133
## 3 3.367 66 0.167
## 4 3.417 64 0.217
## 5 3.450 78 0.250
## 6 3.500 66 0.300
## 7 2.900 63 0.300
## 8 2.883 55 0.317
## 9 3.567 73 0.367
## 10 3.600 79 0.400
(media = mean(head(arrange(treino, distancia), n=10)$waiting))
## [1] 69.6
# k = 10
ggplot(treino, aes(x=eruptions, y=waiting)) +
geom_point() +
annotate("rect", xmin = (3.2 - 0.45), xmax = (3.2 + 0.45),
ymin= 40, ymax=100, alpha=0.2, fill="red") +
annotate("pointrange", x = 3.2, y = media,
ymin = 40, ymax = 100, colour = "red",
size = .5, alpha=0.5) + theme_minimal()
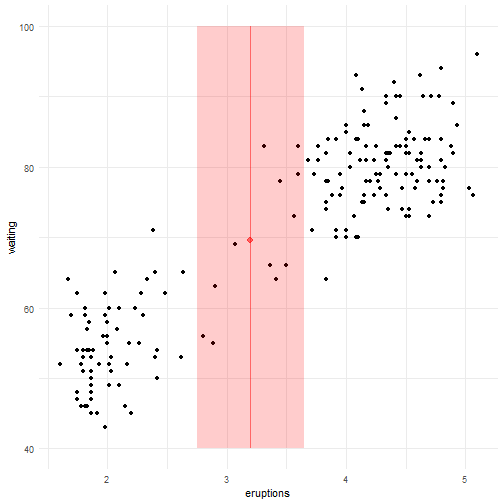
Ou ainda, um k=190
# mostrando as ultimas observações ordenadas pela distancia
tail(arrange(treino, distancia), n=5)
## eruptions waiting distancia
## 188 4.933 86 1.733
## 189 4.933 86 1.733
## 190 5.033 77 1.833
## 191 5.067 76 1.867
## 192 5.100 96 1.900
(media = mean(head(arrange(treino, distancia), n=190)$waiting))
## [1] 70.81053
# k = 190
ggplot(treino, aes(x=eruptions, y=waiting)) +
geom_point() + theme_minimal() +
annotate("rect", xmin= (3.2 -1.85), xmax=(3.2 +1.85),
ymin= 40, ymax=100, alpha=0.2, fill="red") +
annotate("pointrange", x = 3.2, y = media,
ymin = 40, ymax = 100, colour = "red",
size = .5, alpha=0.5)
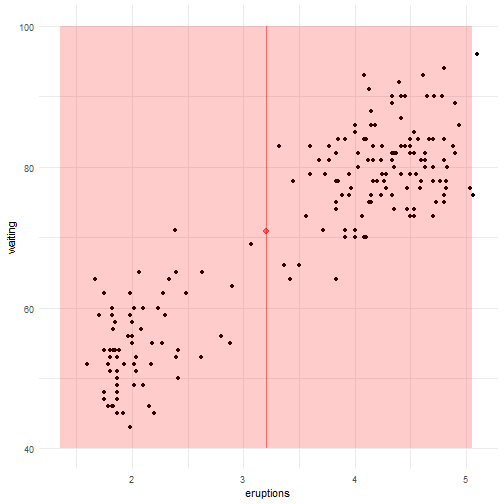
Para bases com mais de uma variável explicativa, o cálculo da distância é feito da mesma forma assim como foi mostrado na parte de classificação.
KNN com o pacote FNN
Agora veremos como utilizar algumas funções do pacote FNN (Fast Nearest Neighbor) para aplicarmos o KNN em um problema de classificação e de regressão. Iremos utilizar bases de dados reais obtidas no repositório de aprendizado de máquina https://archive.ics.uci.edu/ml/index.php.
Em Classificação
Vamos carregar a base de dados transfusion. Essa base contém algumas informações sobre doação de sangue de 748 voluntários. Nossa variável de interesse é a variável “whether.he.she.donated.blood.in.March.2007”, que indica se o paciente doou sangue em março de 2007 ou não (1 - doou, 0 - não doou). As variáveis explicativas são as seguintes:
- Recency..months. - meses desde a última doação de sangue;
- Frequency..times. - número total de doações já realizadas;
- Monetary..c.c..blood. - sangue total já doado em c.c. (centímetros cúbicos);
- Time..months - meses desde a 1ª doação de sangue.
base = readRDS("transfusion.rds")
str(base)
## 'data.frame': 748 obs. of 5 variables:
## $ Recency..months. : num 2 0 1 2 1 4 2 1 2 5 ...
## $ Frequency..times. : int 50 13 16 20 24 4 7 12 9 46 ...
## $ Monetary..c.c..blood. : int 12500 3250 4000 5000 6000 1000 1750 3000 2250 11500 ...
## $ Time..months. : num 98 28 35 45 77 4 14 35 22 98 ...
## $ whether.he.she.donated.blood.in.March.2007: int 1 1 1 1 0 0 1 0 1 1 ...
É importante ressaltar que para aplicação do KNN todas as variáveis explicativas devem ser numéricas. Como isso ocorre na nossa base, vamos prosseguir para a divisão em treino e teste.
# Pegando 80% dos dados para o treino:
set.seed(100)
noTreino = caret::createDataPartition(y = base$whether.he.she.donated.blood.in.March.2007,
p = .8, list = F)
treino = base[noTreino,]
teste = base[-noTreino,]
Como temos que escolher o melhor valor de k para o modelo, não podemos escolhê-lo de forma arbitrária. Sendo assim, vamos pegar uma parte do nosso conjunto de treino e utilizarmos para validação. A validação, como já comentado no capítulo Design de Predição, serve como um “pré-teste”, onde iremos utilizar vários valores diferentes de k nela, e selecionar aquele que otimiza a predição. Esse será o valor utilizado para a amostra teste.
Vamos pegar 20% dos dados para a validação. Dessa forma, temos que pegar 25% da amostra treino, pois ela é 80% dos dados totais ($0,25 \times 0,8 = 0,2$).
set.seed(100)
treino_indices = caret::createDataPartition(y = treino$whether.he.she.donated.blood.in.March.2007,
p = .75, list = F)
Treino = treino[treino_indices,]
validacao = treino[-treino_indices,]
Além disso, temos que separar a variável de interesse das variáveis explicativas.
library(dplyr)
# Pegando o rótulo do conjunto treino:
Treino_label = Treino$whether.he.she.donated.blood.in.March.2007
# Pegando apenas as variáveis explicativas do conjunto treino:
Treino = Treino %>% select(-whether.he.she.donated.blood.in.March.2007)
# Pegando o rótulo da validação:
validacao_label = validacao$whether.he.she.donated.blood.in.March.2007
# Pegando apenas as variáveis explicativas da validação:
validacao = validacao %>% select(-whether.he.she.donated.blood.in.March.2007)
# Pegando o rótulo do conjunto teste:
teste_label = teste$whether.he.she.donated.blood.in.March.2007
# Pegando apenas as variáveis explicativas do conjunto teste:
teste = teste %>% select(-whether.he.she.donated.blood.in.March.2007)
Agora vamos utilizar a função knn() do pacote FNN para predizermos os valores da validação a partir dos valores ímpares de k no intervalo de 1 a 19. É importante ressaltar que essa função só pode ser utilizada para problemas de classificação. Os principais argumentos dessa função são:
- train - conjunto treino sem os rótulos;
- test - conjunto de teste sem os rótulos;
- cl - rótulos do conjunto treino;
- k - valor de k (vizinhos) a serem utilizados.
OBS: caso utilize algum valor par de k na função e houver um empate na classificação de alguma amostra, sua classificação final é decidida de forma aleatória.
# Lista que conterá as matrizes de confusão e medidas de avaliação para cada k utilizado:
matrizes = list()
i = 1
repeat{
set.seed(100)
modelo = FNN::knn(train = Treino, test = validacao, cl = Treino_label, k = i)
matrizes[[i]] = caret::confusionMatrix(modelo, as.factor(validacao_label), positive = "1")
i = i+2
if(i == 21) break
}
matrizes
## [[1]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 92 36
## 1 9 12
##
## Accuracy : 0.698
## 95% CI : (0.6175, 0.7704)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.3337368
##
## Kappa : 0.1887
##
## Mcnemar's Test P-Value : 0.0001063
##
## Sensitivity : 0.25000
## Specificity : 0.91089
## Pos Pred Value : 0.57143
## Neg Pred Value : 0.71875
## Prevalence : 0.32215
## Detection Rate : 0.08054
## Detection Prevalence : 0.14094
## Balanced Accuracy : 0.58045
##
## 'Positive' Class : 1
##
##
## [[2]]
## NULL
##
## [[3]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 97 37
## 1 4 11
##
## Accuracy : 0.7248
## 95% CI : (0.6457, 0.7947)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.1265
##
## Kappa : 0.2313
##
## Mcnemar's Test P-Value : 0.0000005806
##
## Sensitivity : 0.22917
## Specificity : 0.96040
## Pos Pred Value : 0.73333
## Neg Pred Value : 0.72388
## Prevalence : 0.32215
## Detection Rate : 0.07383
## Detection Prevalence : 0.10067
## Balanced Accuracy : 0.59478
##
## 'Positive' Class : 1
##
##
## [[4]]
## NULL
##
## [[5]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 96 39
## 1 5 9
##
## Accuracy : 0.7047
## 95% CI : (0.6245, 0.7765)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.272
##
## Kappa : 0.1695
##
## Mcnemar's Test P-Value : 0.0000006527
##
## Sensitivity : 0.18750
## Specificity : 0.95050
## Pos Pred Value : 0.64286
## Neg Pred Value : 0.71111
## Prevalence : 0.32215
## Detection Rate : 0.06040
## Detection Prevalence : 0.09396
## Balanced Accuracy : 0.56900
##
## 'Positive' Class : 1
##
##
## [[6]]
## NULL
##
## [[7]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 99 39
## 1 2 9
##
## Accuracy : 0.7248
## 95% CI : (0.6457, 0.7947)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.1265
##
## Kappa : 0.2102
##
## Mcnemar's Test P-Value : 0.00000001885
##
## Sensitivity : 0.18750
## Specificity : 0.98020
## Pos Pred Value : 0.81818
## Neg Pred Value : 0.71739
## Prevalence : 0.32215
## Detection Rate : 0.06040
## Detection Prevalence : 0.07383
## Balanced Accuracy : 0.58385
##
## 'Positive' Class : 1
##
##
## [[8]]
## NULL
##
## [[9]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 97 41
## 1 4 7
##
## Accuracy : 0.698
## 95% CI : (0.6175, 0.7704)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.3337
##
## Kappa : 0.1332
##
## Mcnemar's Test P-Value : 0.00000008025
##
## Sensitivity : 0.14583
## Specificity : 0.96040
## Pos Pred Value : 0.63636
## Neg Pred Value : 0.70290
## Prevalence : 0.32215
## Detection Rate : 0.04698
## Detection Prevalence : 0.07383
## Balanced Accuracy : 0.55311
##
## 'Positive' Class : 1
##
##
## [[10]]
## NULL
##
## [[11]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 97 43
## 1 4 5
##
## Accuracy : 0.6846
## 95% CI : (0.6035, 0.7582)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.4692
##
## Kappa : 0.0821
##
## Mcnemar's Test P-Value : 0.00000002976
##
## Sensitivity : 0.10417
## Specificity : 0.96040
## Pos Pred Value : 0.55556
## Neg Pred Value : 0.69286
## Prevalence : 0.32215
## Detection Rate : 0.03356
## Detection Prevalence : 0.06040
## Balanced Accuracy : 0.53228
##
## 'Positive' Class : 1
##
##
## [[12]]
## NULL
##
## [[13]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 97 44
## 1 4 4
##
## Accuracy : 0.6779
## 95% CI : (0.5965, 0.752)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.539
##
## Kappa : 0.056
##
## Mcnemar's Test P-Value : 0.00000001811
##
## Sensitivity : 0.08333
## Specificity : 0.96040
## Pos Pred Value : 0.50000
## Neg Pred Value : 0.68794
## Prevalence : 0.32215
## Detection Rate : 0.02685
## Detection Prevalence : 0.05369
## Balanced Accuracy : 0.52186
##
## 'Positive' Class : 1
##
##
## [[14]]
## NULL
##
## [[15]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 100 45
## 1 1 3
##
## Accuracy : 0.6913
## 95% CI : (0.6105, 0.7643)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.4001
##
## Kappa : 0.0693
##
## Mcnemar's Test P-Value : 0.0000000002298
##
## Sensitivity : 0.06250
## Specificity : 0.99010
## Pos Pred Value : 0.75000
## Neg Pred Value : 0.68966
## Prevalence : 0.32215
## Detection Rate : 0.02013
## Detection Prevalence : 0.02685
## Balanced Accuracy : 0.52630
##
## 'Positive' Class : 1
##
##
## [[16]]
## NULL
##
## [[17]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 100 44
## 1 1 4
##
## Accuracy : 0.698
## 95% CI : (0.6175, 0.7704)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.3337
##
## Kappa : 0.096
##
## Mcnemar's Test P-Value : 0.0000000003825
##
## Sensitivity : 0.08333
## Specificity : 0.99010
## Pos Pred Value : 0.80000
## Neg Pred Value : 0.69444
## Prevalence : 0.32215
## Detection Rate : 0.02685
## Detection Prevalence : 0.03356
## Balanced Accuracy : 0.53672
##
## 'Positive' Class : 1
##
##
## [[18]]
## NULL
##
## [[19]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 101 48
## 1 0 0
##
## Accuracy : 0.6779
## 95% CI : (0.5965, 0.752)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.539
##
## Kappa : 0
##
## Mcnemar's Test P-Value : 0.0000000000117
##
## Sensitivity : 0.0000
## Specificity : 1.0000
## Pos Pred Value : NaN
## Neg Pred Value : 0.6779
## Prevalence : 0.3221
## Detection Rate : 0.0000
## Detection Prevalence : 0.0000
## Balanced Accuracy : 0.5000
##
## 'Positive' Class : 1
##
Note que os modelos que possuem as maiores precisões são os com k = 3 e k = 7, de 0,7248. Porém, como no nosso problema identificar quem doou sangue é mais importante do que identificar aqueles que não doaram, vamos escolher o com maior sensibilidade. Sendo assim, o melhor k é o k = 1, que obteve uma sensibilidade de 0,25.
O KNN com k = 1 é conhecido como The Nearest Neighbor Algorithm.
# Utilizando k = 1 para o conjunto teste:
set.seed(100)
modelo_final = FNN::knn(train = Treino, test = teste, cl = Treino_label, k = 1)
# Obtendo a matriz de confusão e demais medidas de avaliação:
caret::confusionMatrix(modelo_final, as.factor(teste_label), positive = "1")
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 101 23
## 1 15 10
##
## Accuracy : 0.745
## 95% CI : (0.6672, 0.8128)
## No Information Rate : 0.7785
## P-Value [Acc > NIR] : 0.8605
##
## Kappa : 0.1902
##
## Mcnemar's Test P-Value : 0.2561
##
## Sensitivity : 0.30303
## Specificity : 0.87069
## Pos Pred Value : 0.40000
## Neg Pred Value : 0.81452
## Prevalence : 0.22148
## Detection Rate : 0.06711
## Detection Prevalence : 0.16779
## Balanced Accuracy : 0.58686
##
## 'Positive' Class : 1
##
Repare que as medidas de avaliação do modelo não foram tão boas; o valor da precisão, particularmente, foi menor do que a taxa de não informação (No Information Rate), o que não deve acontecer. Sendo assim, esse não é o modelo ideal para essa base.
Vamos realizar o mesmo procedimento para os dados mas dessa vez vamos padronizá-los antes.
# Criando a padronização com a função preProcess() do pacote caret:
padronizacao = caret::preProcess(Treino, method = c("center", "scale"))
# Aplicando a padronização ao conjunto treino:
novo_treino = predict(padronizacao, Treino)
# Aplicando a padronização à validação:
nova_valid = predict(padronizacao, validacao)
# Aplicando a padronização ao teste:
novo_teste = predict(padronizacao, teste)
Agora vamos verificar qual é o melhor k:
matrizes = list()
i = 1
repeat{
set.seed(100)
modelo = FNN::knn(novo_treino, nova_valid, Treino_label, k = i)
matrizes[[i]] = caret::confusionMatrix(modelo, as.factor(validacao_label), positive = "1")
i = i+2
if(i == 21) break
}
matrizes
## [[1]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 88 36
## 1 13 12
##
## Accuracy : 0.6711
## 95% CI : (0.5895, 0.7458)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.607388
##
## Kappa : 0.1387
##
## Mcnemar's Test P-Value : 0.001673
##
## Sensitivity : 0.25000
## Specificity : 0.87129
## Pos Pred Value : 0.48000
## Neg Pred Value : 0.70968
## Prevalence : 0.32215
## Detection Rate : 0.08054
## Detection Prevalence : 0.16779
## Balanced Accuracy : 0.56064
##
## 'Positive' Class : 1
##
##
## [[2]]
## NULL
##
## [[3]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 90 38
## 1 11 10
##
## Accuracy : 0.6711
## 95% CI : (0.5895, 0.7458)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.6073878
##
## Kappa : 0.1166
##
## Mcnemar's Test P-Value : 0.0002038
##
## Sensitivity : 0.20833
## Specificity : 0.89109
## Pos Pred Value : 0.47619
## Neg Pred Value : 0.70312
## Prevalence : 0.32215
## Detection Rate : 0.06711
## Detection Prevalence : 0.14094
## Balanced Accuracy : 0.54971
##
## 'Positive' Class : 1
##
##
## [[4]]
## NULL
##
## [[5]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 96 38
## 1 5 10
##
## Accuracy : 0.7114
## 95% CI : (0.6316, 0.7826)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.2163
##
## Kappa : 0.1938
##
## Mcnemar's Test P-Value : 0.000001061
##
## Sensitivity : 0.20833
## Specificity : 0.95050
## Pos Pred Value : 0.66667
## Neg Pred Value : 0.71642
## Prevalence : 0.32215
## Detection Rate : 0.06711
## Detection Prevalence : 0.10067
## Balanced Accuracy : 0.57941
##
## 'Positive' Class : 1
##
##
## [[6]]
## NULL
##
## [[7]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 95 38
## 1 6 10
##
## Accuracy : 0.7047
## 95% CI : (0.6245, 0.7765)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.272
##
## Kappa : 0.1805
##
## Mcnemar's Test P-Value : 0.000002962
##
## Sensitivity : 0.20833
## Specificity : 0.94059
## Pos Pred Value : 0.62500
## Neg Pred Value : 0.71429
## Prevalence : 0.32215
## Detection Rate : 0.06711
## Detection Prevalence : 0.10738
## Balanced Accuracy : 0.57446
##
## 'Positive' Class : 1
##
##
## [[8]]
## NULL
##
## [[9]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 95 38
## 1 6 10
##
## Accuracy : 0.7047
## 95% CI : (0.6245, 0.7765)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.272
##
## Kappa : 0.1805
##
## Mcnemar's Test P-Value : 0.000002962
##
## Sensitivity : 0.20833
## Specificity : 0.94059
## Pos Pred Value : 0.62500
## Neg Pred Value : 0.71429
## Prevalence : 0.32215
## Detection Rate : 0.06711
## Detection Prevalence : 0.10738
## Balanced Accuracy : 0.57446
##
## 'Positive' Class : 1
##
##
## [[10]]
## NULL
##
## [[11]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 96 37
## 1 5 11
##
## Accuracy : 0.7181
## 95% CI : (0.6387, 0.7887)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.1676
##
## Kappa : 0.2177
##
## Mcnemar's Test P-Value : 0.000001724
##
## Sensitivity : 0.22917
## Specificity : 0.95050
## Pos Pred Value : 0.68750
## Neg Pred Value : 0.72180
## Prevalence : 0.32215
## Detection Rate : 0.07383
## Detection Prevalence : 0.10738
## Balanced Accuracy : 0.58983
##
## 'Positive' Class : 1
##
##
## [[12]]
## NULL
##
## [[13]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 96 37
## 1 5 11
##
## Accuracy : 0.7181
## 95% CI : (0.6387, 0.7887)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.1676
##
## Kappa : 0.2177
##
## Mcnemar's Test P-Value : 0.000001724
##
## Sensitivity : 0.22917
## Specificity : 0.95050
## Pos Pred Value : 0.68750
## Neg Pred Value : 0.72180
## Prevalence : 0.32215
## Detection Rate : 0.07383
## Detection Prevalence : 0.10738
## Balanced Accuracy : 0.58983
##
## 'Positive' Class : 1
##
##
## [[14]]
## NULL
##
## [[15]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 97 36
## 1 4 12
##
## Accuracy : 0.7315
## 95% CI : (0.6529, 0.8008)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.09284
##
## Kappa : 0.255
##
## Mcnemar's Test P-Value : 0.0000009509
##
## Sensitivity : 0.25000
## Specificity : 0.96040
## Pos Pred Value : 0.75000
## Neg Pred Value : 0.72932
## Prevalence : 0.32215
## Detection Rate : 0.08054
## Detection Prevalence : 0.10738
## Balanced Accuracy : 0.60520
##
## 'Positive' Class : 1
##
##
## [[16]]
## NULL
##
## [[17]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 97 35
## 1 4 13
##
## Accuracy : 0.7383
## 95% CI : (0.66, 0.8068)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.0662
##
## Kappa : 0.2784
##
## Mcnemar's Test P-Value : 0.000001556
##
## Sensitivity : 0.27083
## Specificity : 0.96040
## Pos Pred Value : 0.76471
## Neg Pred Value : 0.73485
## Prevalence : 0.32215
## Detection Rate : 0.08725
## Detection Prevalence : 0.11409
## Balanced Accuracy : 0.61561
##
## 'Positive' Class : 1
##
##
## [[18]]
## NULL
##
## [[19]]
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 97 37
## 1 4 11
##
## Accuracy : 0.7248
## 95% CI : (0.6457, 0.7947)
## No Information Rate : 0.6779
## P-Value [Acc > NIR] : 0.1265
##
## Kappa : 0.2313
##
## Mcnemar's Test P-Value : 0.0000005806
##
## Sensitivity : 0.22917
## Specificity : 0.96040
## Pos Pred Value : 0.73333
## Neg Pred Value : 0.72388
## Prevalence : 0.32215
## Detection Rate : 0.07383
## Detection Prevalence : 0.10067
## Balanced Accuracy : 0.59478
##
## 'Positive' Class : 1
##
Para o KNN é extremamente importante padronizarmos os dados antes, pois as medidas das variáveis geralmente estão em escalas diferentes, o que torna as distâncias entre os pontos distorcidas dos seus reais valores.
Podemos notar que, em geral, os modelos melhoraram nas sensibilidades e nas precisões. Vamos utilizar k = 17, que foi o modelo com maior sensibilidade (0,2708) e precisão (0,7383).
# Utilizando k = 17 para o conjunto teste:
set.seed(100)
modelo_final = FNN::knn(novo_treino, novo_teste, Treino_label, k = 17)
# Obtendo a matriz de confusão e demais medidas de avaliação:
caret::confusionMatrix(modelo_final, as.factor(teste_label), positive = "1")
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 110 21
## 1 6 12
##
## Accuracy : 0.8188
## 95% CI : (0.7474, 0.8771)
## No Information Rate : 0.7785
## P-Value [Acc > NIR] : 0.138039
##
## Kappa : 0.3725
##
## Mcnemar's Test P-Value : 0.007054
##
## Sensitivity : 0.36364
## Specificity : 0.94828
## Pos Pred Value : 0.66667
## Neg Pred Value : 0.83969
## Prevalence : 0.22148
## Detection Rate : 0.08054
## Detection Prevalence : 0.12081
## Balanced Accuracy : 0.65596
##
## 'Positive' Class : 1
##
Repare que a precisão melhorou muito (0,8188) e a sensibilidade foi um pouco maior, de 0,3636. Isso significa que 36,36% dos voluntários que doaram sangue em março de 2007 foram identificados.
Em Regressão
Vamos carregar a base de dados Computer_Hardware. Essa base contém algumas informações sobre hardwares de diferentes computadores, entre elas nossa variável de interesse, “PRP”, que representa o desempenho relativo publicado do computador. As demais variáveis são:
- MYCT: tempo de ciclo da máquina em nanossegundos;
- MMIN: memória principal mínima em kilobytes;
- MMAX: memória principal máxima em kilobytes;
- CACH: memória do cachê em kilobytes;
- CHMIN: canais mínimos em unidades;
- CHMAX: canais máximos em unidades.
pc = readRDS("Computer_Hardware.rds")
str(pc)
## 'data.frame': 208 obs. of 7 variables:
## $ MYCT : int 29 29 29 29 26 23 23 23 23 400 ...
## $ MMIN : int 8000 8000 8000 8000 8000 16000 16000 16000 32000 1000 ...
## $ MMAX : int 32000 32000 32000 16000 32000 32000 32000 64000 64000 3000 ...
## $ CACH : int 32 32 32 32 64 64 64 64 128 0 ...
## $ CHMIN: int 8 8 8 8 8 16 16 16 32 1 ...
## $ CHMAX: int 32 32 32 16 32 32 32 32 64 2 ...
## $ PRP : int 269 220 172 132 318 367 489 636 1144 38 ...
Novamente temos todas as variáveis numéricas, então vamos prosseguir para a divisão em treino, validação e teste. Vamos separar 60% dos dados para treino, 20% para validação e 20% para teste.
set.seed(100)
noTreino = caret::createDataPartition(y = pc$PRP, p = .8, list = F)
treino = pc[noTreino,]
teste = pc[-noTreino,]
# Vamos pegar 25% do treino para validação, pois 0,25*0,8 = 0,2 -> 20% dos dados.
set.seed(100)
treino_indices = caret::createDataPartition(y = treino$PRP, p = 0.75, list = F)
Treino = treino[treino_indices,]
validacao = treino[-treino_indices,]
Além disso, devemos separar os rótulos de cada conjunto e as suas variáveis explicativas.
library(dplyr)
# Pegando o rótulo do conjunto treino:
Treino_label = Treino$PRP
# Pegando apenas as variáveis explicativas do conjunto treino:
Treino = Treino %>% select(-PRP)
# Pegando o rótulo da validação:
validacao_label = validacao$PRP
# Pegando apenas as variáveis explicativas da validação:
validacao = validacao %>% select(-PRP)
# Pegando o rótulo do conjunto teste:
teste_label = teste$PRP
# Pegando apenas as variáveis explicativas do conjunto teste:
teste = teste %>% select(-PRP)
Como já comentado anteriormente, é extremamente importante padronizarmos os dados antes de aplicar o KNN, pois as variáveis se encontram em medidas diferentes e isso pode afetar drasticamente as predições do modelo.
# Para padronizarmos utilizamos a função preProcess() do pacote caret:
padronizacao = caret::preProcess(Treino, method = c("center", "scale"))
# Aplicando a padronização ao treino:
novo_treino = predict(padronizacao, Treino)
# Aplicando a padronização à validação:
nova_valid = predict(padronizacao, validacao)
# Aplicando a padronização ao teste:
novo_teste = predict(padronizacao, teste)
Como vamos aplicar o KNN para regressão, precisamos utilizar a função knn.reg() do pacote FNN. Essa função deve ser usada apenas para aplicar o KNN em modelos de regressão. Seus principais argumentos são:
- train - conjunto treino sem os rótulos;
- test - conjunto teste sem os rótulos;
- y - rótulos do conjunto treino;
- k - valor de k (vizinhos) a serem utilizados.
Para avaliação do modelo iremos utilizar a função defaultSummary() do pacote caret, que nos retornará os valores de RMSE, $R^{2}$ e MAE dos modelos. Como a base de dados é menor do que a utilizada para o problema de classificação, vamos utilizar os valores de k apenas até o valor 10. Como as saídas são numéricas, os valores pares de k também estão inclusos no intervalo.
# Lista que conterá as medidas avaliativas de cada modelo:
modelos = list()
for(i in 1:10){
set.seed(100)
modelo = FNN::knn.reg(train = novo_treino, test = nova_valid, y = Treino_label, k = i)
modelos[[i]] = caret::defaultSummary(data.frame(obs = validacao_label, pred = modelo$pred))
}
modelos
## [[1]]
## RMSE Rsquared MAE
## 44.649748 0.781243 31.550000
##
## [[2]]
## RMSE Rsquared MAE
## 34.903080 0.858955 25.900000
##
## [[3]]
## RMSE Rsquared MAE
## 36.6681060 0.8440494 26.1833333
##
## [[4]]
## RMSE Rsquared MAE
## 39.8067205 0.8189399 26.6500000
##
## [[5]]
## RMSE Rsquared MAE
## 40.6152311 0.8088914 26.5750000
##
## [[6]]
## RMSE Rsquared MAE
## 42.0173245 0.7929419 27.2416667
##
## [[7]]
## RMSE Rsquared MAE
## 38.2030691 0.8291316 26.2285714
##
## [[8]]
## RMSE Rsquared MAE
## 40.9843482 0.8052173 27.5781250
##
## [[9]]
## RMSE Rsquared MAE
## 39.7361902 0.8226082 26.8722222
##
## [[10]]
## RMSE Rsquared MAE
## 37.558361 0.840617 25.845000
Podemos notar que o modelo que utiliza k = 2 obteve o menor RMSE e o maior $R^{2}$ dentre os modelos. O menor MAE ficou por conta do k = 10. Sendo assim, o modelo com k = 2 demonstrou ser o melhor para os dados. Então esse é o valor de k que iremos utilizar para a amostra teste.
# Aplicando o KNN com k = 2 no conjunto teste:
set.seed(100)
modelo_final = FNN::knn.reg(train = novo_treino, test = novo_teste, y = Treino_label, k = 2)
modelo_final
## Prediction:
## [1] 297.5 477.0 32.5 61.0 30.0 26.0 26.0 48.0 290.0 170.0 63.0 26.0 14.0 28.5 151.5 107.0 12.0 24.0 15.5
## [20] 99.0 15.5 46.0 127.0 127.0 301.5 170.5 457.5 40.0 121.5 87.0 21.0 24.5 93.5 170.0 302.5 21.0 21.0 33.0
## [39] 37.0 22.0
Agora vamos avaliar o nosso modelo final. Para pegar apenas o vetor com as predições precisamos utilizar o comando “modelo_final$pred”.
caret::defaultSummary(data.frame(obs = teste_label, pred = modelo_final$pred))
## RMSE Rsquared MAE
## 36.755697 0.908051 23.712500
Note que obtivemos um $R^{2}$ acima de 0,9 e o valor do MAE foi um pouco menor do que o do modelo aplicado na validação. O RMSE sofreu um leve aumento, mas como melhoramos 2 das 3 medidas do modelo, pode-se dizer que ele se saiu bem para os dados.
KNN com a função train() do pacote caret
Vamos usar a base de dados Sacramento do pacote caret. Ela contém informações sobre imóveis à venda em Sacramento, Califórnia. Queremos predizer o preço (price) do imóvel baseado no número de quartos (beds), banheiros (baths), tamanho (sqft) e localização (latitude e longitude).
library(caret); library(dplyr)
data("Sacramento")
# por comodidade, vamos deixar apenas as variáveis que serão utilizadas
Sacramento = Sacramento %>%
select(beds, baths, sqft, latitude, longitude, price)
# Fazendo a divisão treino teste
set.seed(1010)
noTreino = createDataPartition(Sacramento$price, p=0.7, list=F)
treino = Sacramento[noTreino,]
teste = Sacramento[-noTreino,]
head(treino)
## beds baths sqft latitude longitude price
## 2 3 1 1167 38.47890 -121.4310 68212
## 4 2 1 852 38.61684 -121.4391 69307
## 5 2 1 797 38.51947 -121.4358 81900
## 6 3 1 1122 38.66260 -121.3278 89921
## 9 2 2 941 38.62119 -121.2706 94905
## 10 3 2 1146 38.70091 -121.4430 98937
Note que a variância das variáveis são bem diferentes. Por exemplo, a variância de beds é 0.7873567 enquanto que a variância de sqft é 527601.7995051. Suponha que temos uma nova observação e vamos começar a calcular as distâncias. Seja a nova observação:
## beds baths sqft latitude longitude
## 1 2 1 836 38.63191 -121.4349
Então, calculando a distância euclidiana entre ela e a primeira observação do conjunto treino temos:
\(\sqrt{(3-1)^{2}+(1-1)^{2}+(1167-836)^{2}+(38.47890-38.63191)^{2}+(-121.4310-(-121.4349))^{2}} =\)
\(\sqrt{(2)^{2}+(0)^{2}+(331)^{2}+(-0.15301)^{2}+(0.0039)^{2}} =\)
Perceba que a influência que a variavel sqft terá sob a distância é muito maior do que a da variavel beds ou longitude por exemplo. Isso pode ser resolvido ao padronizar os dados.
Ao utilizar o método KNN, os dados precisam ser padronizados por causa da influência no cálculo das distâncias.
Sabendo disso, podemos agora treinar nosso modelo.
library(caret)
set.seed(32)
modelo = caret::train(price ~ ., data = treino, method = "knn", tuneLength = 10,
preProcess = c("center", "scale"),
trControl = trainControl(method = "repeatedcv", number=10,repeats=3))
modelo
## k-Nearest Neighbors
##
## 655 samples
## 5 predictor
##
## Pre-processing: centered (5), scaled (5)
## Resampling: Cross-Validated (10 fold, repeated 3 times)
## Summary of sample sizes: 588, 588, 589, 590, 590, 590, ...
## Resampling results across tuning parameters:
##
## k RMSE Rsquared MAE
## 5 83858.89 0.6169478 58564.48
## 7 84351.64 0.6105358 58443.99
## 9 84207.68 0.6124963 57963.02
## 11 84140.90 0.6137614 58033.12
## 13 85045.62 0.6064900 58873.68
## 15 86106.78 0.5969789 59869.60
## 17 86467.75 0.5949395 60504.63
## 19 87061.35 0.5916483 61004.59
## 21 87553.16 0.5879941 61280.41
## 23 87757.07 0.5877060 61537.33
##
## RMSE was used to select the optimal model using the smallest value.
## The final value used for the model was k = 5.
Usando a função train() podemos indicar o valor de k utilizando o argumento tuneLength, onde dizemos uma quantidade n, ele constroi o modelos utilizando os n primeiros valores default e retorna o melhor k baseado na precisão (se for um problema de classificação) ou RMSE (se for um problema de regressão). Também podemos utilizar o tuneGrid = expand.grid(k=) passando um ou mais valores para k e ele testa todos e decide qual é o melhor com o mesmo critério do tuneLenght.
Podemos alterar o critério de escolha do k adicionando o argumento metric="MAE" no train() por exemplo.
plot(modelo)
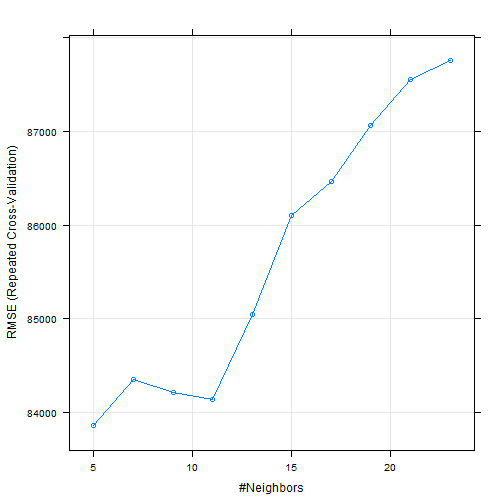
Como podemos ver, k=5 obteve a menor raiz do erro quadrático médio, portanto foi o k escolhido.
# Avaliando o preditor
predicao = predict(modelo, teste)
postResample(predicao,teste$price)
## RMSE Rsquared MAE
## 79186.8548476 0.5920253 58742.4553550
Modelos Lineares
Modelos lineares, também conhecido como regressão linear, é um método estatístico que utiliza a relação existente entre duas ou mais variáveis de modo que uma delas pode ser prevista (explicada) através da outra. Essa relação entre as variáveis deve ser aproximadamente linear para que o modelo possa ser aplicado.
Para vermos o passo-a-passo de como o método funciona, considere o banco de dados a seguir. Ele possui informações sobre o valor das vendas (em U.M.) de 40 empresas e os valores dos seus gastos com propaganda na mídia nacional (em U.M.) e gastos com propaganda por outros meios (em U.M.).
vendas = readRDS("Vendas_Empresas.rds")
head(vendas)
## Venda Prop_outros_meios Prop_nacional
## 1 12.85 5.6 3.8
## 2 11.55 4.1 4.8
## 3 12.78 3.7 3.6
## 4 11.19 4.8 5.2
## 5 9.00 3.4 2.9
## 6 9.34 6.1 3.4
Vamos construir o diagrama de dispersão entre a variável Vendas e as demais.
# Pacote para plotar gráfico de pontos em 3 dimensões:
library(lattice)
cloud(Venda~Prop_outros_meios*Prop_nacional, data = vendas,
xlab = "Prop. Outros Meios", ylab = "Prop. Mídia Nacional",
zlab = "Vendas", main = "Vendas de 40 Empresas baseado nos Gastos com Propagandas")
Podemos observar que há uma relação positiva e aproximadamente linear entre as vendas e os gastos com propagandas na mídia nacional e em outros meios. Ou seja, quanto maior os gastos com propaganda da empresa, maior tende a ser o valor das suas vendas. Sendo assim, podemos propor o seguinte modelo para os dados:
\(Y_i = \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \varepsilon_i; \ i = 1, 2,...n.\) onde:
-
$Y_i$ = valor da variável resposta (Vendas, em u.m.) referente a i-ésima empresa;
-
$X_{i1}$ = gastos com propaganda (em u.m.) por outros meios da i-ésima empresa;
-
$X_{i2}$ = gastos com propaganda (em u.m.) na mídia nacional da i-ésima empresa;
-
$\beta_0$ = coeficiente linear da reta. É o valor das vendas da empresa quando os gastos com propaganda por outros meios e os gastos com propaganda na mídia nacional são iguais a zero;
-
$\beta_1$ = é o quanto aumenta o valor das vendas quando se aumenta em 1 unidade monetária os gastos com propaganda por outros meios;
-
$\beta_2$ = é o quanto aumenta o valor das vendas quando se aumenta em 1 unidade monetária os gastos com propaganda na mídia nacional;
-
$\varepsilon_i$ = erro aleatório do modelo para a i-ésima empresa.
Vamos ajustar um modelo de regressão linar para os dados através da função lm(). Como argumento nós passamos a variável a ser descrita (~) como a combinação linear das outras e o banco de dados onde elas se encontram.
modelo = lm(Venda~Prop_outros_meios+Prop_nacional, data = vendas)
modelo
##
## Call:
## lm(formula = Venda ~ Prop_outros_meios + Prop_nacional, data = vendas)
##
## Coefficients:
## (Intercept) Prop_outros_meios Prop_nacional
## 0.7184 1.5217 0.8145
Repare que o modelo retorna os 3 parâmetros estimados: $\hat{\beta}0$, $\hat{\beta}_1$ e $\hat{\beta}_2$. Eles são estimados através do método dos mínimos quadrados (MQ). Esse método consiste em encontrar os valores de $\beta_0$, $\beta_1$ e $\beta_2$ que minimizam a soma dos quadrados dos erros, isto é, que minimiza $S = \sum\limits{i=1}^{n} \varepsilon_{i}^{2}.$
Para outras informações sobre o ajuste do modelo devemos utilizar a função summary():
summary(modelo)
##
## Call:
## lm(formula = Venda ~ Prop_outros_meios + Prop_nacional, data = vendas)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.5280 -1.0787 0.1309 1.2272 3.5302
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.7184 1.3531 0.531 0.5987
## Prop_outros_meios 1.5217 0.1764 8.628 0.000000000218 ***
## Prop_nacional 0.8145 0.3947 2.063 0.0461 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.868 on 37 degrees of freedom
## Multiple R-squared: 0.7411, Adjusted R-squared: 0.7271
## F-statistic: 52.96 on 2 and 37 DF, p-value: 0.00000000001387
Vamos ver o que cada informação liberada por essa função representa.
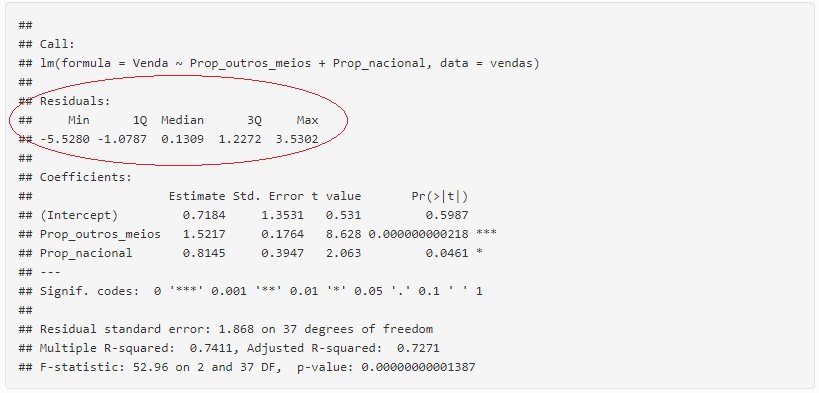
Em Residuals são apresentadas medidas estatísticas sobre os resíduos do modelo: o mínimo, o 1º quartil, a mediana, o 3º quartil e o máximo. Os resíduos são as diferenças entre os valores estimados das vendas das empresas pelo modelo e os valores reais delas.
boxplot(modelo$residuals, col = "lightblue", horizontal = T, xlab = "Resíduos")
Modelos lineares com a função train()
Modelos Lineares Generalizados
Referências
JAMES, G.; Witten, D.; Hastie, T.; TIBSHIRANI, R. An Introduction to Statistical Learning: with applications in R. New York: Springer, 2013.
HASTIE, T.; TIBSHIRANI, R.; FRIEDMAN, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Stanford: Springer, 2008.
PRACTICAL Machine Learning. Coursera. Disponível em https://www.coursera.org/learn/practical-machine-learning. Acesso em 2019.
STARMER, Josh. Machine Learning, 2018. Disponível em https://www.youtube.com/watch?v=Gv9_4yMHFhI&list=PLblh5JKOoLUICTaGLRoHQDuF_7q2GfuJF. Acesso em 2019.
R Core Team (2019). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.
Apêndice
Outras Medidas da Matriz de Confusão
No capítulo de avaliação de preditores introduzimos a matriz de confusão e as medidas de avaliação mais utilizadas: sensibilidade, especificidade e precisão. Vimos também como construí-la de forma rápida e prática com a função confusionMatrix() do pacote caret. Porém, além das 3 medidas mais utilizadas, a função também libera algumas outras, que explicaremos como elas são calculadas a seguir.
Vamos ver a saída da função para o mesmo exemplo dado anteriormente, onde utilizamos a base de dados spam. Nesse exemplo nós treinamos o modelo pelo método GLM e em seguida aplicamos ele ao conjunto teste. Avaliamos o modelo utilizando a matriz de confusão gerada pela função confusionMatrix().
## Confusion Matrix and Statistics
##
## Reference
## Prediction nonspam spam
## nonspam 659 55
## spam 38 398
##
## Accuracy : 0.9191
## 95% CI : (0.9018, 0.9342)
## No Information Rate : 0.6061
## P-Value [Acc > NIR] : < 0.0000000000000002
##
## Kappa : 0.8295
##
## Mcnemar's Test P-Value : 0.09709
##
## Sensitivity : 0.9455
## Specificity : 0.8786
## Pos Pred Value : 0.9230
## Neg Pred Value : 0.9128
## Prevalence : 0.6061
## Detection Rate : 0.5730
## Detection Prevalence : 0.6209
## Balanced Accuracy : 0.9120
##
## 'Positive' Class : nonspam
##
Além de Accuracy (Precisão), Sensitivity (Sensibilidade) e Specificity (Especificidade), as outras saídas representam o seguinte:
-
95% CI = intervalo de confiança com 95% de confiança para a precisão;
-
No Information Rate (Taxa de Não-Informação) = a maior proporção estimada de classe nos dados. Nesse exemplo a taxa foi de 0,6061, o que significa que aproximadamente 60% dos dados são “não spam”, ou seja, se você classificar todos os dados como “não spam” acertará 60% das vezes. Essa taxa pode ser um bom indicador se o seu modelo funciona bem ou não quando comparada à precisão. Caso a taxa seja maior do que a precisão, podemos concluir que o modelo não está funcionando adequadamente para os dados;
-
P-Value [Acc > NIR] = p-valor do teste unilateral onde a hipótese alternativa é: Accuracy > No Information Rate;
-
Mcnemar’s Test P-Value = p-valor do teste de Mcnemar. O teste de Mcnemar é um teste não-paramétrico utilizado em dados nominais pareados. Para mais informações, consulte https://pt.wikipedia.org/wiki/Teste_de_McNemar;
-
Prevalence (Prevalência) = $\frac{VP+FN}{VP+FP+FN+VN}$;
-
Pos Pred Value = $\frac{\hbox{sensibilidade} \times \hbox{prevalência}}{\hbox{sensibilidade} \times \hbox{prevalência} + \left( 1- \hbox{especificidade} \right) \times \left( 1- \hbox{prevalência} \right)}$;
-
Neg Pred Value = $\frac{\hbox{especificidade} \times \left( 1- \hbox{prevalência} \right)}{\left( 1 - \hbox{sensibilidade} \right) \times \hbox{prevalência} + \hbox{especificidade} \times \left( 1 - \hbox{prevalência} \right)}$;
-
Detection Rate (Taxa de Detecção) = $\frac{VP}{VP+FP+FN+VN}$;
-
Detection Prevalence (Prevalência de Detecção) = $\frac{VP+FP}{VP+FP+FN+VN}$;
-
Balanced Accuracy (Precisão Balanceada) = $\frac{\hbox{sensibilidade} + \hbox{especificidade}}{2}$.