Conceitos Gerais de Estatística - Testes de Hipóteses - Parte 1

Importação
import statsmodels.stats as sm
from statsmodels.stats.weightstats import ztest
import scipy.stats as ss
import pandas as pd
import numpy as np
import warnings
from statsmodels.stats.weightstats import ttest_ind
warnings.filterwarnings('ignore')
Na teoria de estimação, vimos que é possível, por meio de estatísticas amostrais adequadas, estimar parâmetros de uma população, dentro de um certo intervalo de confiança. Nos testes de hipóteses, em vez de se construir um intervalo de confiança no qual se espera que o parâmetro da população esteja contido, testa-se a validade de uma afirmação sobre um parâmetro da população. Então, em um teste de hipótese, procura-se tomar decisões a respeito de uma população com base em informações obtidas de uma amostra dessa população.
O contexto em que se baseia a teoria de teste de hipótese é basicamente o mesmo da teoria de estimação por intervalo de confiança. Temos uma população representada por uma variável aleatória X cuja distribuição de probabilidade depende de algum parâmetro θ. O interesse agora está em testar a veracidade de alguma afirmativa sobre θ.
Hipóteses Nula e Alternativa
A hipótese nula, representada por $H_{0}$, é a hipótese básica que queremos testar. Consideraremos apenas hipóteses nulas simples, isto é, hipóteses que estabelecem que o parâmetro de interesse é igual a um determinado valor. A forma geral é:
$H_{0} : θ = θ_{0}$ onde $\theta_0 \in \mathbb{R}$.
Alguns exemplos são:
$H_{0} : µ = 6\space\space\space\space\(H_{0} : p = 0,5\space\space\space\space\space\)H_{0} : σ² = 25$
O procedimento de teste de hipótese resultará em uma regra de decisão que nos permitirá rejeitar ou não rejeitar $H_{0}$. A hipótese alternativa, representada por $H_{1}$, é a hipótese que devemos considerar no caso de rejeição da hipótese nula. A forma mais geral de $H_{1}$ é a hipótese bilateral.
$H_{1} : θ \neq θ_{0}$
Em algumas situações, podemos ter informação que nos permita restringir o domínio da hipótese alternativa.Temos, então, hipóteses unilaterais à esquerda
$H_{1} : θ < θ_{0}$
e hipóteses unilaterais à direita:
$H_{1} : θ > θ_{0}$
A escolha entre essas formas de hipótese alternativa se faz com base no conhecimento sobre o problema sendo considerado e deve ser feita antes de se ter o resultado da amostra.
Exemplos
Exemplo 1: Uma revista X afirmou que o tempo de produção de parafusos de uma máquina da empresa Y é em média de 2 horas. Deseja-se saber se essa afirmação é verdadeira.
Hipótese Nula: $H_{0} : \mu = 2$
Hipótese Alternativa: $H_{1} : \mu\neq 2$
Exemplo 2: Uma empresa afirma que seus funcionários da área de TI possuem idade média maior que 40 anos. Desaja-se saber se essa afirmação é verdadeira.
Hipótese Nula: $H_{0} : \mu = 40$
Hipótese Alternativa: $H_{1} : \mu > 40$
OBS: Vale citar que, são mais utilizadas as hipóteses nulas apenas representadas por igualdades. Porém como forma de interpretação, essa hipótese é associada ao inverso da hipótese alternativa. Tendo como exemplo caso anterior, temos a hipótese nula $H_{0} : \mu = 40$ que pode ser entendida também como $H_{0} : \mu \leq 40$. Pois ao ser realizado um teste para verificar a veracidade da informação, busca-se evidências que a idade média é maior que 40. Caso não há evidências a favor, tem-se que a idade média pode ser menor ou igual a 40.
Estatística de Teste e Regra de Decisão
Assim como na construção dos intervalos de confiança, usaremos uma estatística amostral apropriada para construir o nosso teste de hipótese, e, nesse contexto, essa estatística é chamada estatística de teste. As estatísticas de teste naturalmente dependem do parâmetro envolvido no teste e nesse caso consideraremos os parâmetros média, variância e proporção. O procedimento de decisão será definido em termos da hipótese nula $H_{0}$, com duas decisões possíveis: (i) rejeitar $H_{0}$ ou (ii) não rejeitar $H_{0}$. No quadro a seguir, resumimos as situações possíveis.
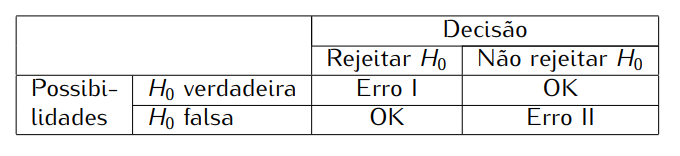
Vemos, aí, que existem duas possibilidades de erro:
- Erro tipo I: rejeitar $H_{0}$ quando $H_{0}$ é verdadeira.
- Erro tipo II: não rejeitar $H_{0}$ quando $H_{0}$ é falsa.
Nível de Significância
Definimos como nível de significância de um teste (geralmente denotado pela letra grega α) a probabilidade do erro tipo 1, ou seja,
\[α \text{ = P(erro I) = P(rejeitar } H_0 | H_0 \text{ é verdadeiro).}\]Em geral é escolhido um dos seguintes valores para α: 1%, 5% e 10%.
P - Valor
O valor P (p-valor) é a probabilidade de se obter um valor da estatística de teste tão ou mais extremo que o valor observado, supondo-se H0 verdadeira.
A partir da definição, podemos definir a regra de decisão do teste através do resultado do p-valor.
- Se p-valor > $\alpha$, não rejeitamos $H_{0}$
- Se p-valor ≤ $\alpha$, rejeitamos $H_{0}$, ou seja, há evidências a favor de $H_{1}$.
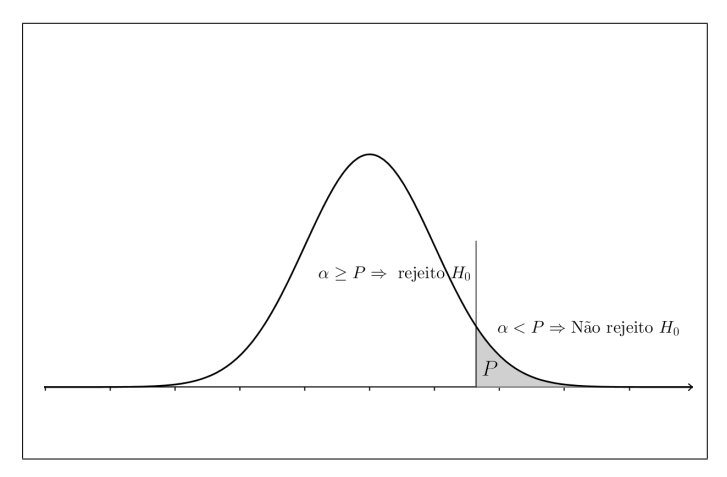
Graças a diversidade de testes disponíveis, esses testes estatísticos podem ser classificados em dois grupos distintos:
- Testes Paramétricos: testes realizados partindo do pressuposto que a população segue uma distribuição normal.
- Testes Não Paramétricos: testes que não precisam partir do pressuposto da normalidade.
A seguir serão apresentados alguns testes estatísticos paramétricos para 1 e 2 populações independentes.
Inferência sobre Uma População
Teste de Hipótese para a Média Populacional
Seja $ X1, . . . , Xn $ uma amostra aleatória de uma população normal com média μ e variância σ² desconhecidas. E suponha que queremos testar as seguintes hipóteses:
$H_{0} : \mu = \mu_{0}$
vs
$H_{1} : \mu < ou > ou \neq \mu_{0}$,
onde $\mu_{0}$ ∈ $\mathbb{R}$.
Seja T a estatística do teste definida por:
T = $\frac{\bar{X}-\mu}{\frac{S}{\sqrt{n}}} \sim t_{n-1}$
onde $ \bar{X} $ e $ S $ são a média amostral e a variância amostral, respectivamente.
Após a definição das hipóteses e da estatística de teste, temos que o p-valor é calculado por:
- Se $H_{1}: \mu \neq \mu_{0}$:
| $p-valor = P (\left | T \right | >\left | T_{obs} \right | \mid H_{0})$ |
- Se $H_{1}: \mu > \mu_{0}$:
$p-valor = P (T > T_{obs}\mid H_{0})$
- Se $H_{1}: \mu < \mu_{0}$:
$p-valor = P (T < T_{obs}\mid H_{0})$
onde
$T_{obs} = \frac{\bar{X}-\mu_{0}}{\frac{S}{\sqrt{n}}}$
Para se aplicar o teste de média para uma população com variância desconhecida, utilizamos a função
ttest_1sampda biblioteca scipy, cujo argumentos de entrada obrigatórios são:
a: a amostra observada.popmean: valor associado a $\mu_{0}$ nas hipóteses.
Nota-se que essa função não possui nenhum argumento de entrada que indique o tipo da hipótese alternativa (unilateral ou bilateral) que será utilizada. Logo, tem-se que essa função retorna apenas o valor do $T_{obs}$ e o p-valor do teste bilateral. Dessa forma, só podem ser aplicados testes cuja hipótese nula seja $\mu \neq \mu_{0}$
Como na biblioteca statsmodels não há função para a utilização das hipóteses unilaterais, iremos também criar a função
ttest_unique retorna o valor de $T_{obs}$ e o p-valor, e possui como argumentos de entrada:
amostra: amostra observada.popmean: valor associado a $\mu_{0}$ nas hipóteses.alternative: tipo da hipótese alternativa desejada: “larger” (unilateral à direita) ou “smaller” (unilateral à esquerda).
def ttest_uni(amostra, popmean, alternative):
n= len(amostra)
tobs = (np.mean(amostra)-popmean)/np.sqrt(np.var(amostra, ddof=1)/n)
if(alternative == "smaller"):
pvalor = ss.t.cdf(tobs,n-1)
if(alternative == "larger"):
pvalor = 1 - ss.t.cdf(tobs,n-1)
print('(%.16f,%.16f)' % (tobs,pvalor))
Agora vamos aplicar alguns exemplos práticos de forma a demonstrar a facilidade da aplicabilidade das funções e dos conceitos estatísticos já apresentados.
Para isso será utilizado um banco de dados que representa uma amostra aleatória simples de 1470 funcionários da empresa IBM.
base=pd.read_csv('R-Employee-Attrition.csv')
base.head()
| Age | Attrition | BusinessTravel | DailyRate | Department | DistanceFromHome | Education | EducationField | EmployeeCount | EmployeeNumber | ... | RelationshipSatisfaction | StandardHours | StockOptionLevel | TotalWorkingYears | TrainingTimesLastYear | WorkLifeBalance | YearsAtCompany | YearsInCurrentRole | YearsSinceLastPromotion | YearsWithCurrManager | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 41 | Yes | Travel_Rarely | 1102 | Sales | 1 | 2 | Life Sciences | 1 | 1 | ... | 1 | 80 | 0 | 8 | 0 | 1 | 6 | 4 | 0 | 5 |
| 1 | 49 | No | Travel_Frequently | 279 | Research & Development | 8 | 1 | Life Sciences | 1 | 2 | ... | 4 | 80 | 1 | 10 | 3 | 3 | 10 | 7 | 1 | 7 |
| 2 | 37 | Yes | Travel_Rarely | 1373 | Research & Development | 2 | 2 | Other | 1 | 4 | ... | 2 | 80 | 0 | 7 | 3 | 3 | 0 | 0 | 0 | 0 |
| 3 | 33 | No | Travel_Frequently | 1392 | Research & Development | 3 | 4 | Life Sciences | 1 | 5 | ... | 3 | 80 | 0 | 8 | 3 | 3 | 8 | 7 | 3 | 0 |
| 4 | 27 | No | Travel_Rarely | 591 | Research & Development | 2 | 1 | Medical | 1 | 7 | ... | 4 | 80 | 1 | 6 | 3 | 3 | 2 | 2 | 2 | 2 |
5 rows × 35 columns
Exemplo 1:
Dado que a idade dos funcionários da empresa IBM que raramente viajam a trabalho segue uma distribuição normal com média e variância desconhecidas. Deseja-se testar se a média das idades dos funcionários que raramente viajam a trabalho pode ser considerada ou não igual a 37 anos, utilizando um nível de significância de 5%.
Através desse problema temos as hipóteses:
$H_{0} : \mu = 37$
vs
$H_{1} : \mu\neq 37$
base_rarely= base[base['BusinessTravel'] == "Travel_Rarely"] # Filtrar apenas os dados dos que raramente viajam a trabalho.
base_rarely.head()
| Age | Attrition | BusinessTravel | DailyRate | Department | DistanceFromHome | Education | EducationField | EmployeeCount | EmployeeNumber | ... | RelationshipSatisfaction | StandardHours | StockOptionLevel | TotalWorkingYears | TrainingTimesLastYear | WorkLifeBalance | YearsAtCompany | YearsInCurrentRole | YearsSinceLastPromotion | YearsWithCurrManager | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 41 | Yes | Travel_Rarely | 1102 | Sales | 1 | 2 | Life Sciences | 1 | 1 | ... | 1 | 80 | 0 | 8 | 0 | 1 | 6 | 4 | 0 | 5 |
| 2 | 37 | Yes | Travel_Rarely | 1373 | Research & Development | 2 | 2 | Other | 1 | 4 | ... | 2 | 80 | 0 | 7 | 3 | 3 | 0 | 0 | 0 | 0 |
| 4 | 27 | No | Travel_Rarely | 591 | Research & Development | 2 | 1 | Medical | 1 | 7 | ... | 4 | 80 | 1 | 6 | 3 | 3 | 2 | 2 | 2 | 2 |
| 6 | 59 | No | Travel_Rarely | 1324 | Research & Development | 3 | 3 | Medical | 1 | 10 | ... | 1 | 80 | 3 | 12 | 3 | 2 | 1 | 0 | 0 | 0 |
| 7 | 30 | No | Travel_Rarely | 1358 | Research & Development | 24 | 1 | Life Sciences | 1 | 11 | ... | 2 | 80 | 1 | 1 | 2 | 3 | 1 | 0 | 0 | 0 |
5 rows × 35 columns
ss.ttest_1samp(base_rarely['Age'],popmean = 37)
Ttest_1sampResult(statistic=0.3183482529054914, pvalue=0.7502845793964478)
Como p-valor = 0.75 é maior que o nível de significância proposto, não rejeitamos a hipótese nula, ou seja, há evidências que a média das idades dos funcionários que raramente viajam a trabalho é igual a 37 anos.
Exemplo 2:
Dado que a idade dos funcionários da empresa IBM que frequentemente viajam a trabalho segue uma distribuição normal com média e variância desconhecidas. Deseja-se testar se a média das idades dos funcionários que frequentemente viajam a trabalho pode ser considerada menor que 39 anos, utilizando um nível de significância de 1%.
Através desse problema temos as hipóteses:
$H_{0} : \mu = 39$
vs
$H_{1} : \mu < 39$
base_freq= base[base['BusinessTravel'] == "Travel_Frequently"] # Filtrar apenas os dados dos que frequentemente viajam a trabalho.
base_freq.head()
| Age | Attrition | BusinessTravel | DailyRate | Department | DistanceFromHome | Education | EducationField | EmployeeCount | EmployeeNumber | ... | RelationshipSatisfaction | StandardHours | StockOptionLevel | TotalWorkingYears | TrainingTimesLastYear | WorkLifeBalance | YearsAtCompany | YearsInCurrentRole | YearsSinceLastPromotion | YearsWithCurrManager | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 49 | No | Travel_Frequently | 279 | Research & Development | 8 | 1 | Life Sciences | 1 | 2 | ... | 4 | 80 | 1 | 10 | 3 | 3 | 10 | 7 | 1 | 7 |
| 3 | 33 | No | Travel_Frequently | 1392 | Research & Development | 3 | 4 | Life Sciences | 1 | 5 | ... | 3 | 80 | 0 | 8 | 3 | 3 | 8 | 7 | 3 | 0 |
| 5 | 32 | No | Travel_Frequently | 1005 | Research & Development | 2 | 2 | Life Sciences | 1 | 8 | ... | 3 | 80 | 0 | 8 | 2 | 2 | 7 | 7 | 3 | 6 |
| 8 | 38 | No | Travel_Frequently | 216 | Research & Development | 23 | 3 | Life Sciences | 1 | 12 | ... | 2 | 80 | 0 | 10 | 2 | 3 | 9 | 7 | 1 | 8 |
| 26 | 32 | Yes | Travel_Frequently | 1125 | Research & Development | 16 | 1 | Life Sciences | 1 | 33 | ... | 2 | 80 | 0 | 10 | 5 | 3 | 10 | 2 | 6 | 7 |
5 rows × 35 columns
ttest_uni(amostra = base_freq['Age'], popmean = 39, alternative = "smaller")
(-4.9557346279446639,0.0000006294162639)
Como p-valor = 0.0000006 é menor que o nível de significância proposto, rejeitamos a hipótese nula, ou seja, há evidências que a média das idades dos funcionários que frequentemente viajam a trabalho é menor do que a 39 anos.
Exemplo 3:
Dado que a idade dos funcionários da empresa IBM do departamento de vendas segue uma distribuição normal com média e variância desconhecidas. Deseja-se testar se a média das idades dos funcionários do departamento de vendas pode ser considerada maior do que 40 anos, utilizando um nível de significância de 10%.
Através desse problema temos as hipóteses:
$H_{0} : \mu = 40$
vs
$H_{1} : \mu> 40$
base_sales= base[base['Department'] == "Sales"] # Filtrar apenas os dados dos funcinários do departamento de vendas.
base_sales.head()
| Age | Attrition | BusinessTravel | DailyRate | Department | DistanceFromHome | Education | EducationField | EmployeeCount | EmployeeNumber | ... | RelationshipSatisfaction | StandardHours | StockOptionLevel | TotalWorkingYears | TrainingTimesLastYear | WorkLifeBalance | YearsAtCompany | YearsInCurrentRole | YearsSinceLastPromotion | YearsWithCurrManager | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 41 | Yes | Travel_Rarely | 1102 | Sales | 1 | 2 | Life Sciences | 1 | 1 | ... | 1 | 80 | 0 | 8 | 0 | 1 | 6 | 4 | 0 | 5 |
| 18 | 53 | No | Travel_Rarely | 1219 | Sales | 2 | 4 | Life Sciences | 1 | 23 | ... | 3 | 80 | 0 | 31 | 3 | 3 | 25 | 8 | 3 | 7 |
| 21 | 36 | Yes | Travel_Rarely | 1218 | Sales | 9 | 4 | Life Sciences | 1 | 27 | ... | 2 | 80 | 0 | 10 | 4 | 3 | 5 | 3 | 0 | 3 |
| 27 | 42 | No | Travel_Rarely | 691 | Sales | 8 | 4 | Marketing | 1 | 35 | ... | 4 | 80 | 1 | 10 | 2 | 3 | 9 | 7 | 4 | 2 |
| 29 | 46 | No | Travel_Rarely | 705 | Sales | 2 | 4 | Marketing | 1 | 38 | ... | 4 | 80 | 0 | 22 | 2 | 2 | 2 | 2 | 2 | 1 |
5 rows × 35 columns
ttest_uni(amostra = base_sales['Age'],popmean = 40, alternative = "larger")
(-8.0835777128154724,0.9999999999999970)
Como o p-valor é maior que o nível de significância proposto, não rejeitamos a hipótese nula, ou seja, não há evidências que a idade média dos funcionários do departamento de vendas seja maior que 40 anos.
Teste de Hipóteses para a Proporção
De posse de uma grande amostra aleatória simples $ X1, X2,…,Xn $ extraída de uma população $X ∼ Ber(p)$, nosso interesse está em testar a hipótese nula
$H_{0} : p = p_{0}$
a um nível de significância α, onde $ p_0 \in (0,1) $. E $ p $ se trata da proporção de elementos de uma população que possuem determinada característica de interesse para o experimento. Dependendo do conhecimento sobre o problema, a hipótese alternativa pode tomar uma das três formas:
$H_{1} : p < ou > ou \neq p_{0}$
Em qualquer dos casos, a estatística de teste baseia-se na proporção amostral; para grandes amostras, sabemos que
$Z = \frac{\hat{p}-p}{\sqrt{\frac{p\left ( 1-p \right )}{n}}} \sim N(0,1)$
Após as definições das hipóteses e da estatística de teste, temos que o p-valor é calculado por:
- Se $H_{1}: p \neq p_{0}$,
| $p-valor = P(Z \geq \left | Z_{obs} \right | \mid H_{0})$ |
- Se $H_{1}: p > p_{0}$,
$p-valor = P (Z > Z_{obs}\mid H_{0})$
- Se $H_{1}: p < p_{0}$,
$p-valor = P (Z < Z_{obs}\mid H_{0})$
onde
$Z_{obs} = \frac{\hat{p}-p_{0}}{\sqrt{\frac{p_{0}\left ( 1 - p_{0} \right )}{n}}}$
Para se aplicar o teste para proporção populacional, utilizamos a função
ztestda biblioteca statsmodels que retorna o $Z_{obs}$ e o p-valor, e possui como argumentos de entrada obrigatórios:
x1: a amostra observada.value: valor associado a $p_{0}$alternative: tipo da hipótese alternativa desejada: “two-sided” (bilateral) , “larger” (unilateral à direita) ou “smaller” (unilateral à esquerda).
Agora vamos aplicar alguns exemplos práticos de forma a demonstrar a aplicabilidade das funções e dos conceitos estatísticos já apresentados.
Utilizaremos o banco de dados dos funcionários da empresa IBM já apresentado anteriormente.
Exemplo 1:
Deseja-se averiguar se é corretar afirmar que 25% dos funcionários do departamento de vendas do IBM passaram por algum problema na empresa, utilizando um nível de significância de 5%.
Através desse problema temos as hipóteses:
$H_{0} : p = 0.25$
vs
$H_{1} : p\neq 0.25$
Tem-se essa informação através da variável Attrition do banco de dados.
base_sales['Attrition'] = base_sales['Attrition'].map({'Yes' : 1, 'No' : 0}) # transformando a variável Risk para valores numéricos
base_sales.head()
| Age | Attrition | BusinessTravel | DailyRate | Department | DistanceFromHome | Education | EducationField | EmployeeCount | EmployeeNumber | ... | RelationshipSatisfaction | StandardHours | StockOptionLevel | TotalWorkingYears | TrainingTimesLastYear | WorkLifeBalance | YearsAtCompany | YearsInCurrentRole | YearsSinceLastPromotion | YearsWithCurrManager | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 41 | 1 | Travel_Rarely | 1102 | Sales | 1 | 2 | Life Sciences | 1 | 1 | ... | 1 | 80 | 0 | 8 | 0 | 1 | 6 | 4 | 0 | 5 |
| 18 | 53 | 0 | Travel_Rarely | 1219 | Sales | 2 | 4 | Life Sciences | 1 | 23 | ... | 3 | 80 | 0 | 31 | 3 | 3 | 25 | 8 | 3 | 7 |
| 21 | 36 | 1 | Travel_Rarely | 1218 | Sales | 9 | 4 | Life Sciences | 1 | 27 | ... | 2 | 80 | 0 | 10 | 4 | 3 | 5 | 3 | 0 | 3 |
| 27 | 42 | 0 | Travel_Rarely | 691 | Sales | 8 | 4 | Marketing | 1 | 35 | ... | 4 | 80 | 1 | 10 | 2 | 3 | 9 | 7 | 4 | 2 |
| 29 | 46 | 0 | Travel_Rarely | 705 | Sales | 2 | 4 | Marketing | 1 | 38 | ... | 4 | 80 | 0 | 22 | 2 | 2 | 2 | 2 | 2 | 1 |
5 rows × 35 columns
ztest(x1 = base_sales['Attrition'], value = 0.25, alternative = "two-sided")
(-2.279392275404384, 0.0226437570988434)
Como p-valor = 0.02 é menor que o nível de significância proposto, rejeitamos a hipótese nula, ou seja, há evidências que a proporção de funcionários que passaram por problemas é diferente de 25%.
Exemplo 2:
Deseja-se averiguar se é corretar afirmar que menos de 30% dos funcionários do departamento de pesquisa do IBM passaram por algum problema na empresa, utilizando um nível de significância de 10%.
Através desse problema temos as hipóteses:
$H_{0} : p = 0.3$
vs
$H_{1} : p< 0.3$
base_pesq= base[base['Department'] == "Research & Development"] # Filtrar apenas os dados dos funcinários do departamento de vendas.
base_pesq['Attrition'] = base_pesq['Attrition'].map({'Yes' : 1, 'No' : 0})
base_pesq.head()
| Age | Attrition | BusinessTravel | DailyRate | Department | DistanceFromHome | Education | EducationField | EmployeeCount | EmployeeNumber | ... | RelationshipSatisfaction | StandardHours | StockOptionLevel | TotalWorkingYears | TrainingTimesLastYear | WorkLifeBalance | YearsAtCompany | YearsInCurrentRole | YearsSinceLastPromotion | YearsWithCurrManager | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 49 | 0 | Travel_Frequently | 279 | Research & Development | 8 | 1 | Life Sciences | 1 | 2 | ... | 4 | 80 | 1 | 10 | 3 | 3 | 10 | 7 | 1 | 7 |
| 2 | 37 | 1 | Travel_Rarely | 1373 | Research & Development | 2 | 2 | Other | 1 | 4 | ... | 2 | 80 | 0 | 7 | 3 | 3 | 0 | 0 | 0 | 0 |
| 3 | 33 | 0 | Travel_Frequently | 1392 | Research & Development | 3 | 4 | Life Sciences | 1 | 5 | ... | 3 | 80 | 0 | 8 | 3 | 3 | 8 | 7 | 3 | 0 |
| 4 | 27 | 0 | Travel_Rarely | 591 | Research & Development | 2 | 1 | Medical | 1 | 7 | ... | 4 | 80 | 1 | 6 | 3 | 3 | 2 | 2 | 2 | 2 |
| 5 | 32 | 0 | Travel_Frequently | 1005 | Research & Development | 2 | 2 | Life Sciences | 1 | 8 | ... | 3 | 80 | 0 | 8 | 2 | 2 | 7 | 7 | 3 | 6 |
5 rows × 35 columns
ztest(x1 = base_pesq['Attrition'], value = 0.30, alternative = "smaller")
(-14.499935934146963, 6.063151045772378e-48)
Como p-valor é menor do que o nível de significância proposto, rejeitamos $ H_0 $, ou seja, há evidências que a proporção de funcionários do departamento de vendas que passaram por algum problema é menos de 30%.
Exemplo 3:
Deseja-se averiguar se é corretar afirmar que mais de 60% dos funcionários do IBM que frequentemente viajam a trabalho passaram por algum problema na empresa, utilizando um nível de significância de 1%.
Através desse problema temos as hipóteses:
$H_{0} : p = 0.6$
vs
$H_{1} : p > 0.6$
base_freq['Attrition'] = base_freq['Attrition'].map({'Yes' : 1, 'No' : 0})
base_freq.head()
| Age | Attrition | BusinessTravel | DailyRate | Department | DistanceFromHome | Education | EducationField | EmployeeCount | EmployeeNumber | ... | RelationshipSatisfaction | StandardHours | StockOptionLevel | TotalWorkingYears | TrainingTimesLastYear | WorkLifeBalance | YearsAtCompany | YearsInCurrentRole | YearsSinceLastPromotion | YearsWithCurrManager | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 49 | 0 | Travel_Frequently | 279 | Research & Development | 8 | 1 | Life Sciences | 1 | 2 | ... | 4 | 80 | 1 | 10 | 3 | 3 | 10 | 7 | 1 | 7 |
| 3 | 33 | 0 | Travel_Frequently | 1392 | Research & Development | 3 | 4 | Life Sciences | 1 | 5 | ... | 3 | 80 | 0 | 8 | 3 | 3 | 8 | 7 | 3 | 0 |
| 5 | 32 | 0 | Travel_Frequently | 1005 | Research & Development | 2 | 2 | Life Sciences | 1 | 8 | ... | 3 | 80 | 0 | 8 | 2 | 2 | 7 | 7 | 3 | 6 |
| 8 | 38 | 0 | Travel_Frequently | 216 | Research & Development | 23 | 3 | Life Sciences | 1 | 12 | ... | 2 | 80 | 0 | 10 | 2 | 3 | 9 | 7 | 1 | 8 |
| 26 | 32 | 1 | Travel_Frequently | 1125 | Research & Development | 16 | 1 | Life Sciences | 1 | 33 | ... | 2 | 80 | 0 | 10 | 5 | 3 | 10 | 2 | 6 | 7 |
5 rows × 35 columns
ztest(x1 = base_freq['Attrition'], value = 0.6, alternative = "larger")
(-13.47921476827307, 1.0)
Como p-valor = 1 é maior que o nível de significância proposto, não rejeitamos a hipótese nula, ou seja, não há evidências de que mais de 60% dos funcionários que frequentemente viajam a trabalho tenham tido alguma complicação na empresa.
Teste de Hipóteses para a Variância
Seja $ X1, X2,…,Xn $ uma amostra aleatória de uma população com distribuição normal, com média μ e variância σ² desconhecidas.
E suponha que estamos interessados em testar as hipóteses
$H_{o}: \sigma^{2} = \sigma^{2}_{0}$
vs
$H_{1}: \sigma^{2} < ou > ou \neq \sigma^{2}_{0}$,
,
onde $σ_{0}^{2}$ > 0.
Em qualquer dos casos, a estatística de teste Q é dada por:
$Q = \frac{(n-1)S^{2}}{\sigma^{2}}\sim \chi^{2}_{(n-1)}$
Após as definições das hipóteses e da estatística de teste, temos que o p-valor é calculado por:
- Se $H_{1}: \sigma^{2} \neq \sigma^{2}_{0}$,
$p-valor = 2\times min \left { P(Q < Q_{obs}\mid H_{0}),P (Q > Q_{obs}\mid H_{0}) \right }$
- Se $H_{1}: \sigma^{2} > \sigma^{2}_{0}$,
$p-valor = P (Q > Q_{obs}\mid H_{0})$
- Se $H_{1}: \sigma^{2} < \sigma^{2}_{0}$,
$p-valor = P (Q < Q_{obs}\mid H_{0})$
onde
$Q_{obs} = \frac{(n-1)S^{2}}{\sigma_{0}^{2}}$
Como não há funções pertencentes às bibliotecas statsmodels e scipy que realizam o teste para a variância, criamos uma função própria chamada
test_varque retorna o $Q_{obs}$ e o p-valor, e recebe como argumentos de entrada:
amostra: amostra observada.sigma2: valor referente a $\sigma^{2}_{0}$alternative: tipo da hipótese alternativa desejada: “two-sided” (bilateral) , “larger” (unilateral à direita) ou “smaller” (unilateral à esquerda).
def test_var (amostra, sigma2, alternative= "two.sided"):
n=len(amostra)
qobs= (n-1)*np.var(amostra, ddof=1)/sigma2
if(alternative == "smaller"):
pvalor = ss.chi2.cdf(qobs,n-1)
if(alternative == "larger"):
pvalor = 1 - ss.chi2.cdf(qobs,n-1)
if(alternative == "two.sided"):
pvalor = 2*np.minimum(1 - ss.chi2.cdf(qobs,n-1),ss.chi2.cdf(qobs,n-1))
print('(%.16f,%.16f)' % (qobs,pvalor))
Agora vamos aplicar alguns exemplos práticos de forma a demonstrar a facilidade da aplicabilidade das funções e dos conceitos estatísticos já apresentados. Utilizaremos o banco de dados dos funcionários da empresa IBM.
Exemplo 1:
Um dos diretores da empresa IBM afirmou que a variabilidade da idade dentre seus funcionários é de 76 anos². Dado que a idade dos funcionários segue uma distribuição normal com média e variância desconhecidas, deseja-se averiguar a veracidade da afirmação, utilizando um nível de significância de 1%.
Através desse problema temos as hipóteses:
$H_{0} : \sigma^{2} = 76$
vs
$H_{1} : \sigma^{2} \neq 76$
Nesse caso não é preciso realizar nenhum processo de filtragem, ou seja, utilzaremos a base original.
test_var(amostra = base['Age'], sigma2 = 76, alternative = "two.sided")
(1613.0982456140357044,0.0096419873719233)
Como p-valor = 0.009 é menor que o nível de significância proposto, rejeitamos a hipótese nula, ou seja, temos evidências de que a variabilidade das idades dos funcionários é diferente de 76. Portanto a afirmação é considerada equivocada.
Exemplo 2:
Um jornal local noticiou que a variabilidade dos anos de trabalho dos funcionários da empresa IBM é inferior a 60 anos². Dado que os anos de trabalho dos funcionários da empresa IBM segue uma distribuição normal com média e variância desconhecidas, deseja-se averiguar a veracidade da afirmação, utilizando um nível de significância de 5%.
Através desse problema temos as hipóteses:
$H_{0} : \sigma^{2} = 60$
vs
$H_{1} : \sigma^{2} < 60$
Nesse caso, também não é preciso realizar nenhum processo de filtragem, ou seja, utilizaremos a base original.
test_var(base['TotalWorkingYears'],60,"smaller")
(1482.2347959183696275,0.6009205627661879)
Como p-valor = 0.6 é maior que o nível de significância proposto, não rejeitamos a hipótese nula, ou seja, não há evidências que a variabilidade dos anos de trabalho dos funcionários seja inferior a 60. Portanto, considera-se que a informação noticiada é incorreta.
Exemplo 3:
Um dos funcionários da empresa afirmou que a variabilidade dos anos de trabalho dos funcionários da empresa IBM casados é superior a 30 anos². Dado que os anos de trabalho dos funcionários casados da empresa IBM segue uma distribuição normal com média e variância desconhecidas, deseja-se averiguar a veracidade da afirmação, utilizando um nível de significância de 10%.
Através desse problema temos as hipóteses:
$H_{0} : \sigma^{2} = 30$
vs
$H_{1} : \sigma^{2} > 30$
Podemos achar essa informação através da variável MaritalStatus presente no banco de dados.
base_casados = base[base['MaritalStatus'] == "Married"]
base_casados.head()
| Age | Attrition | BusinessTravel | DailyRate | Department | DistanceFromHome | Education | EducationField | EmployeeCount | EmployeeNumber | ... | RelationshipSatisfaction | StandardHours | StockOptionLevel | TotalWorkingYears | TrainingTimesLastYear | WorkLifeBalance | YearsAtCompany | YearsInCurrentRole | YearsSinceLastPromotion | YearsWithCurrManager | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 49 | No | Travel_Frequently | 279 | Research & Development | 8 | 1 | Life Sciences | 1 | 2 | ... | 4 | 80 | 1 | 10 | 3 | 3 | 10 | 7 | 1 | 7 |
| 3 | 33 | No | Travel_Frequently | 1392 | Research & Development | 3 | 4 | Life Sciences | 1 | 5 | ... | 3 | 80 | 0 | 8 | 3 | 3 | 8 | 7 | 3 | 0 |
| 4 | 27 | No | Travel_Rarely | 591 | Research & Development | 2 | 1 | Medical | 1 | 7 | ... | 4 | 80 | 1 | 6 | 3 | 3 | 2 | 2 | 2 | 2 |
| 6 | 59 | No | Travel_Rarely | 1324 | Research & Development | 3 | 3 | Medical | 1 | 10 | ... | 1 | 80 | 3 | 12 | 3 | 2 | 1 | 0 | 0 | 0 |
| 9 | 36 | No | Travel_Rarely | 1299 | Research & Development | 27 | 3 | Medical | 1 | 13 | ... | 2 | 80 | 2 | 17 | 3 | 2 | 7 | 7 | 7 | 7 |
5 rows × 35 columns
test_var(amostra = base_casados['TotalWorkingYears'], sigma2 = 50, alternative = "larger")
(834.6771471025249411,0.0000173254449680)
Como p-valor = 0.00001 é menor que o nível de significância proposto, rejeitamos a hipótese nula, ou seja há evidências que a variabilidade dos anos trabalhados entre os casados é superior a 30.Portanto a afirmação realizada é dada como verdadeira.
Inferência sobre Duas Populações
Teste de Hipóteses para Comparação de Duas Proporções
Sejam \({X_{1} \sim N(\mu_{1}, \sigma^2_{1})}\) e \({X_{2} \sim N(µ_{2}, σ^2_{2})}\) duas amostras independentes de tamanho \({n_{1}}\) e \({n_{2}}\), respectivamente, e \({ \hat{p_{1}} }\) e \({ \hat{p_{2}} }\) estimadores de \({p_{1}}\) e \({p_{2}}\), proporção de ocorrência de um certo evento. Então, aproximadamente, \({\hat{p_{1}} \sim N\left ( p_{1}, \frac{p_{1}(1 - p_{1})}{n_{1}} \right )}\) e \({\hat{p_{2}} \sim N\left ( p_{2}, \frac{p_{2}(1 - p_{2})}{n_{2}} \right )}\) implicando \({\hat{p_{1}} - \hat{p_{2}} \sim N\left ( p_{1} - p_{2}, \frac{p_{1}(1 - p_{1})}{n_{1}}+ \frac{p_{2}(1 - p_{2})}{n_{2}} \right )}\). Portanto:
$Z = \frac{(\hat{p_{1}} - \hat{p_{2}}) - (p_{1} - p_{2})}{\sqrt{\frac{\hat{p_{1}}(1 - \hat{p_{1}})}{n_{1}} + \frac{\hat{p_{2}}(1 - \hat{p_{2}})}{n_{2}}}} \sim N(0, 1)$
Para realizar o teste da comparação de duas proporções, existem 3 formas de propor as hipóteses nula e alternativa:
$H_{0}: p_{1} - p_{2} = p_{0} \ \ \times \ \ H_{1}: p_{1} - p_{2} \neq p_{0}$
ou
$H_{0}: p_{1} - p_{2} = p_{0} \ \ \times \ \ H_{1}: p_{1} - p_{2} > p_{0}$
ou
$H_{0}: p_{1} - p_{2} = p_{0} \ \ \times \ \ H_{1}: p_{1} - p_{2} < p_{0}$
onde $ p_0 \in (0,1) $.
Através da estatística de teste e a definição das hipóteses, para a tomada de decisão é preciso calcular o p-valor, cujas fórmulas são dadas por:
- Se $H_{1} : p_{X} - p_{Y}\neq p_{0}$,
$p-valor = P(|Z| \geq \left | Z_{obs} \right |\mid H_{0})$
- Se $H_{1} : p_{X} - p_{Y} > p_{0}$,
$p-valor = P(Z > Z_{obs}\mid H_{0} )$
- Se $H_{1} : p_{X} - p_{Y} < p_{0}$, $p-valor = P(Z < Z_{obs}\mid H_{0} )$
onde
$Z_{obs} = \frac{(\hat{p}{1} - \hat{p}{2}) - p_{0}}{\sqrt{\frac{\hat{p}{1}(1 - \hat{p}{1})}{n_{1}} + \frac{\hat{p}{2}(1 - \hat{p}{2})}{n_{2}}}}$
Para realizar esses cálculos no Python, utilizaremos a função
ztest()da biblioteca statsmodels, já apresentado anteriormente, com os seguintes argumentos de entrada:
x1: a amostra observada.x2: a segunda amostra observada.value: valor associado a $p_{0}$alternative: tipo da hipótese alternativa desejada: “two-sided” (bilateral) , “larger” (unilateral à direita) ou “smaller” (unilateral à esquerda).
Agora vamos aplicar alguns exemplos práticos de forma a demonstrar a aplicabilidade das funções e dos conceitos estatísticos já apresentados. Utilizaremos um banco de dados que representa uma amostra aleatória simples de 562 filmes lançados no cinema no período de 2007 a 2011, com informações como gênero, orçamento e críticas presentes no site Rotten Tomatoes.
df = pd.read_csv('Movie-Ratings.csv')
df.head()
| Film | Genre | Rotten Tomatoes Ratings % | Audience Ratings % | Budget (million $) | Year of release | |
|---|---|---|---|---|---|---|
| 0 | (500) Days of Summer | Comedy | 87 | 81 | 8 | 2009 |
| 1 | 10,000 B.C. | Adventure | 9 | 44 | 105 | 2008 |
| 2 | 12 Rounds | Action | 30 | 52 | 20 | 2009 |
| 3 | 127 Hours | Adventure | 93 | 84 | 18 | 2010 |
| 4 | 17 Again | Comedy | 55 | 70 | 20 | 2009 |
Exemplo 1
Deseja-se avaliar se no período de 2007 a 2011, a proporção de filmes de Comédia lançados no cinema foi igual a proporção de filmes de Aventura, utilizando um nível de significância de 5%.
As hipóteses serão as seguintes:
$H_{0} : p_{X} - p_{Y} = 0$
vs
$H_{1} : p_{X} - p_{Y}\neq 0$
Onde X são filmes do gênero Comédia e Y, os filmes do gênero Aventura.
df['Genre_Comedy'] = np.where(df.Genre == "Comedy", 1, 0)
df['Genre_Adventure'] = np.where(df.Genre == "Adventure", 1, 0)
df.head()
| Film | Genre | Rotten Tomatoes Ratings % | Audience Ratings % | Budget (million $) | Year of release | Genre_Comedy | Genre_Adventure | |
|---|---|---|---|---|---|---|---|---|
| 0 | (500) Days of Summer | Comedy | 87 | 81 | 8 | 2009 | 1 | 0 |
| 1 | 10,000 B.C. | Adventure | 9 | 44 | 105 | 2008 | 0 | 1 |
| 2 | 12 Rounds | Action | 30 | 52 | 20 | 2009 | 0 | 0 |
| 3 | 127 Hours | Adventure | 93 | 84 | 18 | 2010 | 0 | 1 |
| 4 | 17 Again | Comedy | 55 | 70 | 20 | 2009 | 1 | 0 |
ztest(x1=df.Genre_Comedy, x2= df.Genre_Adventure, value = 0, alternative = 'two-sided')
(11.789438693301005, 4.42480180658489e-32)
Como o p-valor é menor que o nível de significância proposto, rejeitamos $ H_0 $, ou seja, há evidências que as proporções de filmes de Comédia e de Aventura lançados no período de 2007 a 2011 nos cinema sejam diferentes.
Exemplo 2
Baseado no resultado do exemplo anterior, sabe-se que as proporções de filmes de comédia e aventura em 2007-2011 são consideradas diferentes. Então, através disso, deseja-se avaliar se a proporção de filmes de Comédia é maior que a proporção de filmes de Aventura lançados nos cinemas em 2007-2011, utilizando um nível de significância de 1%.
As hipóteses serão as seguintes:
$H_{0} : p_{X} - p_{Y} = 0$
vs
$H_{1} : p_{X} - p_{Y} > 0$ $\Rightarrow$ $H_{1} : p_{X} > p_{Y}$
Onde X são filmes do gênero Comédia e Y, os filmes do gênero Aventura.
ztest(x1=df.Genre_Comedy, x2=df.Genre_Adventure, value = 0, alternative = 'larger')
(11.789438693301005, 2.212400903292445e-32)
Como p-valor é menor que o nível de significância proposto, rejeitamos $ H_0 $, ou seja, há evidências que foram lançados mais filmes do gênero Comédia do que filmes do gênero Aventura nos cinemas no período de 2007 a 2011.
Teste de Hipótese para Razão das Variâncias
Sejam ${X_1 \sim N(µ_{1}, σ^2{1})}$ e ${X_2 \sim N(µ{2}, σ^2{2})}$ duas amostras independentes de tamanho ${n{1}}$ e ${n_{2}}$, respectivamente, e ${S^2{1}}$ e ${S^2{2}}$ suas variâncias amostrais. Então,
$F = \frac{\frac{S^{2}{1}}{S^{2}{2}}}{\frac{\sigma^{2}{1}}{\sigma ^{2}{2}}} \sim F_{n_{1} - 1, n_{2} - 1}$
Para realizar o teste para razão de duas variâncias, existem 3 formas de propor as hipóteses nula e alternativa:
$H_{0}: \frac{\sigma^{2}_{1}}{\sigma^{2}_{2}} = \sigma^{2}_{0} \ \ \times \ \ H_{1}: \frac{\sigma^{2}_{1}}{\sigma^{2}_{2}} \neq \sigma^{2}_{0}$
ou
$H_{0}: \frac{\sigma^{2}_{1}}{\sigma^{2}_{2}} = \sigma^{2}_{0} \ \ \times \ \ H_{1}: \frac{\sigma^{2}_{1}}{\sigma^{2}_{2}} < \sigma^{2}_{0}$
ou
$H_{0}: \frac{\sigma^{2}_{1}}{\sigma^{2}_{2}} = \sigma^{2}_{0} \ \ \times \ \ H_{1}: \frac{\sigma^{2}_{1}}{\sigma^{2}_{2}} > \sigma^{2}_{0}$
Através da estatística de teste e a definição das hipóteses, para a tomada de decisão é preciso calcular o p-valor, cujas fórmulas são dadas por:
-
Se $H_{1} : \frac{\sigma^2{X}}{\sigma^2{Y}}\neq \sigma^2{0}$ $p-valor = 2\times min\left { P\left ( F \geq F{obs} \mid H_{0}\right ), P\left ( F \leq F_{obs} \mid H_{0}\right ) \right }$
-
Se $H_{1} : \frac{\sigma^2{X}}{\sigma^2{Y}}< \sigma^2{0}$ $p-valor = P\left ( F < F{obs}\mid H_{0} \right )$
-
Se $H_{1} : \frac{\sigma^2{X}}{\sigma^2{Y}}> \sigma^2{0}$ $p-valor = P\left ( F > F{obs} \mid H_{0}\right )$
onde
$F_{obs} = \frac{\frac{S^{2}{1}}{S^{2}{2}}}{\frac{\sigma^{2}{1}}{\sigma ^{2}{2}}}$
Infelizmente, assim como no caso de uma população, o Python não possui função para avaliar a razão das variâncias. Por isso, construímos a nossa própria função, cujos argumentos de entrada são:
x1: primeira amostra;x2: segunda amostra;value: valor de ${\sigma^{2}_{0}}$;alternative: ‘two-sided’ (default): H1: razão das variâncias é diferente quevalue; ‘larger’: H1: razão das variâncias é maior quevalue; ‘smaller’: H1: razão das variâncias é menor quevalue.
Essa função retorna a estatística de teste F e o p-valor calculado.
# razão das variâncias
def rvar_test(x1, x2, value, alternative):
stattest = (np.var(x1)/np.var(x2))/value
if alternative == 'smaller':
pvalor = ss.f.cdf(stattest, len(x1) - 1, len(x2) - 1)
elif alternative == 'larger':
pvalor = 1 - ss.f.cdf(stattest, len(x1) - 1, len(x2) - 1)
elif alternative == 'two-sided':
pvalor = 2*ss.f.cdf(stattest, len(x1) - 1, len(x2) - 1)
if pvalor >= 1:
pvalor = 1
print('(%.16f,%.16f)' % (stattest,pvalor))
Agora vamos aplicar alguns exemplos práticos de forma a demonstrar a facilidade da aplicabilidade da função e dos conceitos estatísticos já apresentados. Utilizaremos o banco de dados de avaliações de filmes.
Exemplo 1
Dado que os orçamentos dos filmes de Ação e Aventura seguem distribuições normais com médias e variâncias desconhecidas. Deseja-se avaliar, ao nível de significância de 5%, se a razão das variâncias dos orçamentos dos filmes de Ação e Aventura é igual a 1. Ou seja, verificar se as variâncias são iguais.
As hipótetes serão as seguintes:
$H_{0} : \frac{\sigma^2{X}}{\sigma^2{Y}} = 1$
vs
$H_{1} : \frac{\sigma^2{X}}{\sigma^2{Y}}\neq 1$
Onde X são os orçamentos dos filmes de Ação e Y, os orçamentos dos filmes de Aventura.
df_acao, df_adventure = df[df["Genre"] == 'Action'], df[df["Genre"] == 'Adventure']
rvar_test(x1 = df_acao['Budget (million $)'], x2 = df_adventure['Budget (million $)'],value = 1, alternative = 'two-sided')
(1.1885458719831832,1.0000000000000000)
Como p-valor = 1 é maior que o nível se significância proposto, de 0,05, não rejeitamos a hipótese nula. Ou seja, há evidências de que as variâncias são iguais.
Teste de Hipótese para Comparação de Médias para Duas Populações Independentes
Sejam ${X \sim N(µ_{X}, σ^2{X})}$ e ${Y \sim N(µ{Y}, σ^2_{Y})}$ duas amostras independentes com variâncias desconhecidas. Se, ao relizarmos o teste da razão das variâncias, constatarmos que as variâncias são iguais, teremos o seguinte caso:
$T = \frac{ (\bar{X} - \bar{Y}) - \mu }{ \sqrt{S^2{comb} \left ( \frac{1}{n{X}} + \frac{1}{n_{Y}} \right ) } } \sim t_{n_{X} + n_{Y} - 2}$
Onde,
$S^{2}{comb} = \frac{(n{X} - 1)S^2{X} + (n{Y} - 1)S^2{Y}}{n{X} + n_{Y} - 2}$
Se, ao relizarmos o teste da razão das variâncias, constatarmos que as variâncias são diferentes, teremos o seguinte caso:
$T = \frac{ (\bar{X} - \bar{Y}) - \mu }{ \sqrt{ \frac{S^2{X}}{n{X}} + \frac{S^2{Y}}{n{Y}} } } \sim t_{v}$
Onde,
$v = \frac{ \left ( \frac{s^2{X}}{n{X}} + \frac{s^2{Y}}{n{Y}} \right )^2 }{ \frac{1}{n_{X} - 1}\left ( \frac{s^2{X}}{n{X}} \right )^2 + \frac{1}{n_{Y} - 1}\left ( \frac{s^2{Y}}{n{Y}} \right )^2 }$
Para realizar o teste da comparação de duas médias, existem 3 formas de propor as hipóteses nula e alternativa:
$H_{0}: \mu_{X} - \mu_{Y} = \mu_{0} \ \ \times \ \ H_{1}: \mu_{X} - \mu_{Y} \neq \mu_{0}$
ou
$H_{0}: \mu_{1} - \mu_{2} = \mu_{0} \ \ \times \ \ H_{1}: \mu_{1} - \mu_{2} > \mu_{0}$
ou
$H_{0}: \mu_{1} - \mu_{2} = \mu_{0} \ \ \times \ \ H_{1}: \mu_{1} - \mu_{2} < \mu_{0}$
Dada as estatísticas de teste e a definição das hipóteses, é preciso calcular o p-valor para a tomada de decisão, cujas fórmulas são dadas por:
- Se $H_{1}: \mu_{X} - \mu_{Y} \neq \mu_{0}$,
| $p-valor = P\left ( | T | > \left | T_{obs} \right | \mid H_{0} \right)$ |
-
Se $H_{1}: \mu_{X} - \mu_{Y} > \mu_{0}$,
$p-valor = P\left ( T > T_{obs} \mid H_{0}\right )$
-
Se $H_{1}: \mu_{X} - \mu_{Y} < \mu_{0}$,
$p-valor = P\left ( T < T_{obs} \mid H_{obs} \right )$
onde
$T_{obs} = \frac{ (\bar{X} - \bar{Y}) - \mu_{0} }{ \sqrt{S^2{comb} \left ( \frac{1}{n{X}} + \frac{1}{n_{Y}} \right ) } }$
quando as variâncias são iguais, ou
$T_{obs} = \frac{ (\bar{X} - \bar{Y}) - \mu_{0} }{ \sqrt{ \frac{S^2{X}}{n{X}} + \frac{S^2{Y}}{n{Y}} } }$
quando as variâncias são diferentes.
Para realizar esses cálculos no Python, utilizaremos a função
ttest_ind()da biblioteca statsmodels, cujos argumentos de entrada são:
x1: amostra X.x2: amostra Y.value: valor de ${\mu_{0}}$.alternative: ‘two-sided’ (default): H1: diferença entre as médias é diferente quevalue; ‘larger’: H1: diferença entre as médias é maior quevalue; ‘smaller’: H1: diferença entre as médias é menor quevalue.usevar: ‘pooled’ se as variâncias são iguais, ‘unequal’ se as variâncias são diferentes.
Essa função retornará a estatística de teste, o pvalor e os graus de liberdade, respectivamente.
Agora vamos aplicar alguns exemplos práticos de forma a demonstrar a facilidade da aplicabilidade da função e dos conceitos estatísticos já apresentados. Utilizaremos o banco de dados de avaliações de filmes.
Exemplo 1
Queremos avaliar se a média dos orçamentos dos filmes de Ação e Aventura são iguais, ao nível de significância de 5%:
As hipóteses serão as seguintes:
$H_{0} : \mu_{X} - \mu_{Y} = 0$
vs
$H_{1} : \mu_{X} - \mu_{Y}\neq 0$
Onde X são os orçamentos dos filmes de Ação e Y, os orçamentos dos filmes de Aventura.
Primeiro iremos aplicar o teste de razão de variâncias rvar_test para testar a igualdade entre elas. Utilize também o nível de significância de 5%
rvar_test(x1 = df_acao["Budget (million $)"],x2 = df_adventure["Budget (million $)"],value=1,alternative="two-sided")
(1.1885458719831832,1.0000000000000000)
Como p-valor=1 sendo maior que o nível de significância proposto, há evidências de que as varianças são iguais. Agora aplicaremos o teste de comparação de médias considerando as variâncias iguais.
ttest_ind(x1 = df_acao["Budget (million $)"],x2 = df_adventure["Budget (million $)"], alternative = 'two-sided', usevar = 'pooled', value = 0)
(0.24627191134923368, 0.8057508151994627, 181.0)
Como p-valor= 0.80 é maior que no nível de significância proposto, não rejeitamos a hipótese nula, ou seja, há evidências de que os orçamentos dos filmes de Ação e Aventura são iguais.
Exemplo 2
A revista “The Hollywood Reporter” afirmou que a média dos orçamentos dos filmes de Ação é superior à média dos orçamentos dos filmes de Comédia. Deseja-se avaliar a veracidade dessa informação, ao nível de significância de 5%.
As hipóteses serão as seguintes:
$H_{0} : \mu_{X} - \mu_{Y} = 0$
vs
$H_{1} : \mu_{X} - \mu_{Y}\ > 0$ $\Rightarrow$ $H_{1} : \mu_{X} > \mu_{Y}$
Onde X são os orçamentos dos filmes de Ação e Y, os orçamentos dos filmes de Comédia.
df_comedia = df[df["Genre"] == 'Comedy']
df_comedia.head()
| Film | Genre | Rotten Tomatoes Ratings % | Audience Ratings % | Budget (million $) | Year of release | Genre_Comedy | Genre_Adventure | |
|---|---|---|---|---|---|---|---|---|
| 0 | (500) Days of Summer | Comedy | 87 | 81 | 8 | 2009 | 1 | 0 |
| 4 | 17 Again | Comedy | 55 | 70 | 20 | 2009 | 1 | 0 |
| 6 | 27 Dresses | Comedy | 40 | 71 | 30 | 2008 | 1 | 0 |
| 8 | 30 Minutes or Less | Comedy | 43 | 48 | 28 | 2011 | 1 | 0 |
| 9 | 50/50 | Comedy | 93 | 93 | 8 | 2011 | 1 | 0 |
Primeiro iremos aplicar o teste de razão de variâncias rvar_test para testar a igualdade entre elas. Utilize o nível de significância de 5%.
rvar_test(x1 = df_acao["Budget (million $)"], x2= df_comedia["Budget (million $)"],value=1,alternative="larger")
(5.6148884065672879,0.0000000000000001)
Como o p-valor é menor que o nível de significância proposto, temos que as variâncias são diferentes. Agora realizaremos o teste de comparação de médias considerando variâncias diferentes.
ttest_ind(x1 = df_acao["Budget (million $)"],x2 = df_comedia["Budget (million $)"], alternative = 'two-sided', usevar = 'unequal', value = 0)
(8.765572657433554, 7.820570304870018e-16, 201.07797410706948)
Como p-valor é menor que o nível de significância proposto, rejeitamos a hipótese nula, ou seja, há evidências de que a média dos orçamentos dos filmes de Ação é superior à média dos orçamentos dos filmes de Comédia.
Teste de Hipótese para Comparação de Médias para Duas Populações Dependentes
Sejam ${X \sim N(µ_{X}, σ^2{X})}$ e ${Y \sim N(µ{Y}, σ^2{Y})}$ duas amostras pareadas tal que consideramos os pares ${(X{1}, Y_{1}), \ …, \ (X_{n}, Y_{n})}$. Definindo ${D = X - Y}$, temos que ${D \sim N(µ_{D}, σ^2{D})}$, com ${µ{d} = µ_{X} - µ_{Y}}$. Assim,
$T= \frac{\bar{D} - \mu}{\sqrt{\frac{S^2{D}}{n}}} \sim t{n-1}$
onde,
$D_{i} = X_{i} - Y_{i}$
e
$\bar{D} = \sum_{i = 1}^{n} \frac{D_{i}}{n}$
Assim como nos outros casos, existirão 3 hipóteses possíveis, e suas formas de calcular o pvalor:
$H_{0}: \mu_{D} = \mu_{0} \ \ \times \ \ H_{1}: \mu_{D} \neq \mu_{0}$
ou
$H_{0}: \mu_{D} = \mu_{0} \ \ \times \ \ H_{1}: \mu_{D} > \mu_{0}$
ou
$H_{0}: \mu_{D} = \mu_{0} \ \ \times \ \ H_{1}: \mu_{D} < \mu_{0}$
- Se $H_{1}: \mu_{D} \neq \mu_{0}$,
| $p-valor = P (\left | T \right | >\left | T_{obs} \right | \mid H_{0})$ |
-
Se $H_{1}: \mu_{D} > \mu_{0}$,
$p-valor = P (T > T_{obs}\mid H_{0})$
-
Se $H_{1}: \mu_{D} < \mu_{0}$,
$p-valor = P (T < T_{obs}\mid H_{0})$
onde
$T_{obs}= \frac{\bar{D} - \mu_{0}}{\sqrt{\frac{S^2_{D}}{n}}}$
Definindo ${D = X - Y}$, temos o caso de Teste de Hipótese para Média de uma população. Portanto, após obtermos D, podemos aplicar as funções ttest_1samp e ttest_uni já apresentadas no material.
Para aplicações, utilizaremos o banco de dados que representa uma amostra aleatória simples de 198 pessoas. Essa base representa um experimento sobre os efeitos do medicamento ansiolíticos na utilização da memória.
data = pd.read_csv("Islander_data.csv")
data.head()
| first_name | last_name | age | Happy_Sad_group | Dosage | Drug | Mem_Score_Before | Mem_Score_After | Diff | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Bastian | Carrasco | 25 | H | 1 | A | 63.5 | 61.2 | -2.3 |
| 1 | Evan | Carrasco | 52 | S | 1 | A | 41.6 | 40.7 | -0.9 |
| 2 | Florencia | Carrasco | 29 | H | 1 | A | 59.7 | 55.1 | -4.6 |
| 3 | Holly | Carrasco | 50 | S | 1 | A | 51.7 | 51.2 | -0.5 |
| 4 | Justin | Carrasco | 52 | H | 1 | A | 47.0 | 47.1 | 0.1 |
Exemplo 1
Um experimento foi realizado com moradores de diversas ilhas, onde foi possível testar os efeitos de remédios ansiolíticos no uso da memória. Sabendo que os tempos dos testes de memória, antes e depois, dos moradores expostos ao medicamento A seguem uma distribuição normal com média e variância desconhecidas, deseja-se avaliar se a droga Aafeta o uso da memória, seja positivamente ou negativamente, observando a diferença do tempo do teste de memória antes e depois da exposição ao medicamento, ao nível de significância de5%.
As hipótetes serão as seguintes:
$H_{0} : \mu_{X} - \mu_{Y} = 0$ $\Rightarrow$ $H_{0} : \mu_{D} = 0$
vs
$H_{1} : \mu_{X} - \mu_{Y} \neq 0$ $\Rightarrow$ $H_{1} : \mu_{D} \neq 0$
Onde D é a diferença entre o tempo de resposta do teste depois (X) e antes (Y) do uso da droga A.
data_A = data[data['Drug'] == 'A']
data_A.head()
| first_name | last_name | age | Happy_Sad_group | Dosage | Drug | Mem_Score_Before | Mem_Score_After | Diff | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Bastian | Carrasco | 25 | H | 1 | A | 63.5 | 61.2 | -2.3 |
| 1 | Evan | Carrasco | 52 | S | 1 | A | 41.6 | 40.7 | -0.9 |
| 2 | Florencia | Carrasco | 29 | H | 1 | A | 59.7 | 55.1 | -4.6 |
| 3 | Holly | Carrasco | 50 | S | 1 | A | 51.7 | 51.2 | -0.5 |
| 4 | Justin | Carrasco | 52 | H | 1 | A | 47.0 | 47.1 | 0.1 |
Utilizaremos a variável Diff que já contém os valores das diferenças dos tempos de resposta dos testes de memórias, sendo calculado da forma: Diff = Mem_Score_After - Mem_Score_Before.
ss.ttest_1samp(a = data_A['Diff'], popmean = 0)
Ttest_1sampResult(statistic=5.848567939730841, pvalue=1.6898179935298675e-07)
Como p-valor é menor que no nível de significância proposto, rejeitamos a hipótese nula, ou seja, há evidências de que o medicamento afeta, seja positivamente ou negativamente, o uso da memória.
Exemplo 2
Dado que no exemplo anterior as médias dos tempos foram considerados diferentes, iremos avaliar se a droga A afeta o uso da memória positivamente, ao nível de significância de1%.
As hipótetes serão as seguintes:
$H_{0} : \mu_{X} - \mu_{Y} = 0$ $\Rightarrow$ $H_{0} : \mu_{D} = 0$
vs
$H_{1} : \mu_{X} - \mu_{Y} > 0$ $\Rightarrow$ $H_{1} : \mu_{D} > 0$
Onde D é a diferença entre o tempo de resposta do teste depois (X) e antes (Y) do uso da droga A.
ttest_uni(amostra = data_A['Diff'],popmean = 0, alternative = "larger")
(5.8485679397308408,0.0000000844908996)
Como p-valor é menor que o nível de significância proposto, rejeitamos a hipótese nula, ou seja, há evidências de que o tempo de resposta do teste depois do uso do medicamento foi maior do que antes. Portanto, tem-se que o medicamento A afeta positivamente o uso da memória.
Referências
FARIAS, A. M. L. Apostila de Estatística II. Departamento de Estatística. 2017. Universidade Federal Fluminense. Velarde, L. G. C. CAVALIERE, Y. F. Apostila Inferência Estatística. Departamento de Estatística. Universidade Federal Fluminense