library(caret)
library(kernlab)
data(spam)
set.seed(371)
noTreino = createDataPartition(y = spam$type, p = 0.75, list = F)6 Avaliando Preditores - Introdução ao Pacote Caret
O pacote caret (abreviação de Classification And Regression Training) é um pacote muito útil para apricar os métodos de aprendizado de máquinas pois envolve algoritmos que possibilitam que as previsões sejam feitas de forma mais prática, simplificando o processo de criação de modelos preditivos. Neste guia detalhado pode ser encontrado mais informações sobre o pacote.
6.1 Avaliando Classificadores
Vamos utilizar a base de dados spam novamente para realizarmos o procedimento de predição para um e-mail (se ele é spam ou não spam), dessa vez utilizando o pacote caret.
Para fazer a separação da amostra em treino e teste, vamos particionar a base de dados com a função createDataPartition(). Em problemas de classificação, a função createDataPartition() garante que a mesma proporção de cada classe observada no banco de dados seja mantida nas amostras de treino e teste. Ou seja, se o banco de dados tiver 70% de elementos do tipo A e 30% do tipo B, as amostras treino e teste terão cada uma 70% de elementos do tipo A e 30% do tipo B.
Para problemas de regressão, createDataPartition() cria uma partição estratificada com base na variável dependente contínua, dividindo os dados de forma a representar bem a distribuição dos valores da variável de resposta em ambas as amostras de treino e teste.
Essa função retorna os números das linhas a serem selecionadas para o treino. Os principais argumentos são:
y = é a variável resposta; será mantida a mesma proporção de cada classe nos conjuntos treino e teste. Para o nosso exemplo, será a variável type. Sendo assim, tanto no treino como no teste teremos a mesma proporção de e-mails spam e não spam.
p = porcentagem da amostra que será utilizada para o treino. Para o nosso exemplo, escolhemos 75%, mas a decisão final é do pesquisador.
list = argumento do tipo logical, se TRUE → os resultados serão mostrados em uma lista, se FALSE → os resultados serão mostrados em uma matriz.
OBS: Esse comando deve ser utilizado apenas quando os dados são amostras independentes.
Agora vamos separar as amostras que irão para o conjunto de treino e as que irão para o conjunto de teste.
# Separando as linhas para o treino:
treino = spam[noTreino,]
# Separando as linhas para o teste:
teste = spam[-noTreino,]Após feita a separação das amostras treino e teste, podemos realizar o treinamento do modelo. Para isso é preciso escolher um dos modelos para ser utilizado. Uma lista com todos os modelos implementados no pacote caret pode ser vista com o seguinte comando:
names(getModelInfo()) [1] "ada" "AdaBag" "AdaBoost.M1"
[4] "adaboost" "amdai" "ANFIS"
[7] "avNNet" "awnb" "awtan"
[10] "bag" "bagEarth" "bagEarthGCV"
[13] "bagFDA" "bagFDAGCV" "bam"
[16] "bartMachine" "bayesglm" "binda"
[19] "blackboost" "blasso" "blassoAveraged"
[22] "bridge" "brnn" "BstLm"
[25] "bstSm" "bstTree" "C5.0"
[28] "C5.0Cost" "C5.0Rules" "C5.0Tree"
[31] "cforest" "chaid" "CSimca"
[34] "ctree" "ctree2" "cubist"
[37] "dda" "deepboost" "DENFIS"
[40] "dnn" "dwdLinear" "dwdPoly"
[43] "dwdRadial" "earth" "elm"
[46] "enet" "evtree" "extraTrees"
[49] "fda" "FH.GBML" "FIR.DM"
[52] "foba" "FRBCS.CHI" "FRBCS.W"
[55] "FS.HGD" "gam" "gamboost"
[58] "gamLoess" "gamSpline" "gaussprLinear"
[61] "gaussprPoly" "gaussprRadial" "gbm_h2o"
[64] "gbm" "gcvEarth" "GFS.FR.MOGUL"
[67] "GFS.LT.RS" "GFS.THRIFT" "glm.nb"
[70] "glm" "glmboost" "glmnet_h2o"
[73] "glmnet" "glmStepAIC" "gpls"
[76] "hda" "hdda" "hdrda"
[79] "HYFIS" "icr" "J48"
[82] "JRip" "kernelpls" "kknn"
[85] "knn" "krlsPoly" "krlsRadial"
[88] "lars" "lars2" "lasso"
[91] "lda" "lda2" "leapBackward"
[94] "leapForward" "leapSeq" "Linda"
[97] "lm" "lmStepAIC" "LMT"
[100] "loclda" "logicBag" "LogitBoost"
[103] "logreg" "lssvmLinear" "lssvmPoly"
[106] "lssvmRadial" "lvq" "M5"
[109] "M5Rules" "manb" "mda"
[112] "Mlda" "mlp" "mlpKerasDecay"
[115] "mlpKerasDecayCost" "mlpKerasDropout" "mlpKerasDropoutCost"
[118] "mlpML" "mlpSGD" "mlpWeightDecay"
[121] "mlpWeightDecayML" "monmlp" "msaenet"
[124] "multinom" "mxnet" "mxnetAdam"
[127] "naive_bayes" "nb" "nbDiscrete"
[130] "nbSearch" "neuralnet" "nnet"
[133] "nnls" "nodeHarvest" "null"
[136] "OneR" "ordinalNet" "ordinalRF"
[139] "ORFlog" "ORFpls" "ORFridge"
[142] "ORFsvm" "ownn" "pam"
[145] "parRF" "PART" "partDSA"
[148] "pcaNNet" "pcr" "pda"
[151] "pda2" "penalized" "PenalizedLDA"
[154] "plr" "pls" "plsRglm"
[157] "polr" "ppr" "pre"
[160] "PRIM" "protoclass" "qda"
[163] "QdaCov" "qrf" "qrnn"
[166] "randomGLM" "ranger" "rbf"
[169] "rbfDDA" "Rborist" "rda"
[172] "regLogistic" "relaxo" "rf"
[175] "rFerns" "RFlda" "rfRules"
[178] "ridge" "rlda" "rlm"
[181] "rmda" "rocc" "rotationForest"
[184] "rotationForestCp" "rpart" "rpart1SE"
[187] "rpart2" "rpartCost" "rpartScore"
[190] "rqlasso" "rqnc" "RRF"
[193] "RRFglobal" "rrlda" "RSimca"
[196] "rvmLinear" "rvmPoly" "rvmRadial"
[199] "SBC" "sda" "sdwd"
[202] "simpls" "SLAVE" "slda"
[205] "smda" "snn" "sparseLDA"
[208] "spikeslab" "spls" "stepLDA"
[211] "stepQDA" "superpc" "svmBoundrangeString"
[214] "svmExpoString" "svmLinear" "svmLinear2"
[217] "svmLinear3" "svmLinearWeights" "svmLinearWeights2"
[220] "svmPoly" "svmRadial" "svmRadialCost"
[223] "svmRadialSigma" "svmRadialWeights" "svmSpectrumString"
[226] "tan" "tanSearch" "treebag"
[229] "vbmpRadial" "vglmAdjCat" "vglmContRatio"
[232] "vglmCumulative" "widekernelpls" "WM"
[235] "wsrf" "xgbDART" "xgbLinear"
[238] "xgbTree" "xyf" Para o nosso exemplo, vamos utilizar regressão logística, que possui no caret a alcunha “glm” (Generalized Linear Model). É um modelo clássico da Estatística, mas que é conhecido por sua grande eficiência para tarefas de classificação, mesmo quando comparado a outros algoritmos exclusivos do ramo de Aprendizado de Máquinas. Dito isso, é também um modelo de classificação, então o seu uso aqui será para exemplificar como se faz para avaliar a qualidade através da Matriz de Confusão.
Agora vamos criar o nosso modelo, utilizando apenas a amostra treino. Para isso vamos usar o comando train().
modelo = train(type ~ ., data = treino, method = "glm")No primeiro argumento colocamos qual variável estamos tentando prever em função de qual(is). No nosso caso, queremos prever “type” em função (“~”) de todas as outras, por isso utilizamos o ponto “.”. Em seguida dizemos de qual base de dados queremos construir o modelo e por último o método de treinamento utilizado.
Caso deseje utilizar apenas algumas das variáveis explicativas, basta detalhar quais variáveis devem ser consideradas no modelo, como o exemplo abaixo:
modelo2 = train(type ~ your+money+capitalAve, data = treino, method = "glm")Agora vamos dar uma olhada como ficou nosso modelo.
modeloGeneralized Linear Model
3451 samples
57 predictor
2 classes: 'nonspam', 'spam'
No pre-processing
Resampling: Bootstrapped (25 reps)
Summary of sample sizes: 3451, 3451, 3451, 3451, 3451, 3451, ...
Resampling results:
Accuracy Kappa
0.9224544 0.8365594Podemos observar que utilizamos uma amostra de tamanho 3451 no treino e 57 variáveis para prever a qual classe um e-mail pertence, spam ou não spam. O que a função faz é ajustar o modelo selecionado (glm no nosso caso) nos dados de treino, buscando otimizar uma métrica pré determinada (o padrão para classificação é acurácia). Quando o modelo necessita de ajuste de hiperparâmetros, a função utiliza métodos de reamostragem para selecionar o melhor modelo. O padrão é reamostragem por bootstrapping com 25 replicações. Trataremos deste tema posteriormente.
Uma vez que ajustamos o modelo podemos aplicá-lo na amostra teste, para estimarmos a acurácia do classificador. Para isso utilizamos o comando predict(). Dentro da função nós passamos o modelo que ajustamos no treino e em qual base de dados gostaríamos de realizar a predição.
predicao = predict(modelo, newdata = teste)
head(predicao, n=30) [1] spam spam spam spam spam spam spam nonspam nonspam
[10] spam spam spam nonspam nonspam spam spam spam spam
[19] spam spam spam spam spam spam spam spam spam
[28] spam spam spam
Levels: nonspam spamAo fazermos isso obtemos uma série de predições para as classes dos e-mails do conjunto teste. Podemos então realizar a avaliação do modelo comparando os resultados da predição com as reais classes dos e-mails, por meio do comando confusionMatrix().
6.1.1 Matriz de Confusão (Confusion Matrix)
A matriz de confusão é a matriz de comparação feita após a predição, onde as linhas correspondem ao que foi previsto e as colunas correspondem à verdade conhecida.
Exemplo: A matriz de confusão para o problema de predição dos e-mails em spam ou não spam fica da seguinta forma:
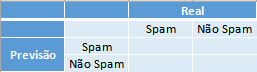
Onde na primeira coluna se encontram os elementos que possuem a característica de interesse (os e-mails que são spam), e, respectivamente nas linhas, os que foram corretamente identificados - o qual são chamados de Verdadeiros Positivos (VP) - e os que foram erroneamente identificados - os Falsos Negativos (FP). Na segunda coluna se encontram os elementos que não possuem a característica de interesse (os e-mails que são ham) e, respectivamente nas linhas, os que foram erroneamente identificados - o qual são chamados de Falsos Positivos (FN) - e os que foram corretamente identificados - os Verdadeiros Negativos (VN).
Com as devidas classificações a matriz de confusão fica da seguinte forma:
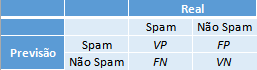
Dentro da função passamos as predições que obtemos pelo modelo ajustado e as reais classificações dos e-mails do conjunto teste.
confusionMatrix(predicao, teste$type)Confusion Matrix and Statistics
Reference
Prediction nonspam spam
nonspam 659 55
spam 38 398
Accuracy : 0.9191
95% CI : (0.9018, 0.9342)
No Information Rate : 0.6061
P-Value [Acc > NIR] : < 2e-16
Kappa : 0.8295
Mcnemar's Test P-Value : 0.09709
Sensitivity : 0.9455
Specificity : 0.8786
Pos Pred Value : 0.9230
Neg Pred Value : 0.9128
Prevalence : 0.6061
Detection Rate : 0.5730
Detection Prevalence : 0.6209
Balanced Accuracy : 0.9120
'Positive' Class : nonspam
A função retorna a matriz de confusão e alguns dados estatísticos, como por exemplo a Acurácia (Accuracy), o Intervalo de Confiança com 95% de confiança (95% CI), a Sensibilidade (Sensitivity), Especificidade (Specificity), entre outros.
Podemos notar que o GLM foi um bom modelo de treinamento para os nossos dados pois obtivemos altas taxas de acertos: uma acurácia de 0,94, 0,96 de sensitividade e 0,90 de especificidade. Vamos ver melhor algumas dessas estatísticas:
Definição (Sensibilidade): A sensibilidade de um método de predição é a porcentagem dos elementos da amostra que possuem a característica de interesse e foram corretamente identificados. Para o nosso exemplo dos e-mails, a sensabilidade é a porcentagem dos e-mails que são spam e foram classificados pelo nosso algoritmo de predição como spam.
Ou seja, podemos escrever \(Sensibilidade = \frac{VP}{VP+FN}\)
Definição (Especificidade): A especificidade de um método de predição é a porcentagem dos elementos da amostra que não possuem a característica de interesse e foram corretamente identificados. Para o nosso exemplo dos e-mails, a especificidade é a porcentagem dos e-mails que são “ham” e o algoritmo de predição os classificou como tal.
Ou seja, podemos escrever \(Especificidade = \frac{VN}{VN+FP}\)
Quando obtemos as sensibilidades e as especificidades de diferentes preditores, naturalmente surge o questionamente: qual deles é melhor para estimar as verdadeiras características de interesse? A resposta depende do que é mais importante para o problema.
Se identificar corretamente os positivos for mais importante, utilizamos o preditor com maior sensibilidade. Se identificar corretamente os negativos for mais importante, utilizamos o preditor com maior especificidade.
Outra medida para avaliar a qualidade do nosso preditor é a acurácia (Accuracy). Ela avalia a porcentagem de acertos que tivemos em geral. Ou seja, somamos o número de Verdadeiros Positivos com o número de Verdadeiros Negativos e dividimos pelo tamanho da amostra. \(Acurácia = \frac{VP+VN}{VP+VN+FN+FP}\)
Para demais medidas da matriz de confusão consulte o [apêndice].
6.2 Avaliando Regressores
Agora vamos utilizar a base de dados faithful para tentar prever o tempo de espera (waiting) entre uma erupção e outra de um gêiser dado a duração das erupções (eruption).
data("faithful")
head(faithful) eruptions waiting
1 3.600 79
2 1.800 54
3 3.333 74
4 2.283 62
5 4.533 85
6 2.883 55Primeiro, vamos separar a amostra em treino e teste.
set.seed(39)
noTreino = createDataPartition(y=faithful$waiting, p=0.7, groups = 5, list=F)
treino = faithful[noTreino,]; teste = faithful[-noTreino,]Quando o argumento y é numérico, a amostra é dividida em grupos com base nos percentis e é feita uma amostragem estratificada. O número de percentis é definido pelo argumento groups.
Agora temos que treinar nosso modelo. Para esse exemplo vamos usar a Regressão Linear (LM - Linear Regression).
Os métodos disponíveis e seus usos podem ser encontrados no guia do caret.
Vamos treinar nosso modelo utilizando a amostra treino.
modelo = caret::train(waiting~eruptions, data = treino, method = "lm")Novamente, colocamos a variável que tentamos prever em função das outras. No caso, só temos duas variáveis então não precisamos colocar o ponto como no [classificador].
modeloLinear Regression
192 samples
1 predictor
No pre-processing
Resampling: Bootstrapped (25 reps)
Summary of sample sizes: 192, 192, 192, 192, 192, 192, ...
Resampling results:
RMSE Rsquared MAE
6.060639 0.805468 4.948071
Tuning parameter 'intercept' was held constant at a value of TRUEPodemos ver que temos 192 observações no conjunto treino e 1 preditor.
Agora vamos aplicar nosso modelo na amostra teste para avaliar o erro dele.
predicao = predict(modelo, newdata = teste)Assim como no classificador, a função predict nos retorna a previsão dos tempos entre as erupções dado os tempos das durações das erupções.
6.2.1 MSE
Assim como há diversas formas de compararmos a qualidade dos classificadores, há também diversas formas de compararmos regressores. O que estudaremos agora é o MSE (mean squared error - erro quadrático médio). Mais formas de comparação de regressores também serão vistas futuramente.
O MSE é a média de quanto os valores previstos para as observações se distanciaram dos valores verdadeiros dessa observação. Obtemos ele somando essas distâncias entre os valores previstos e os reais ao quadrado e dividindo por n.
\[ MSE = \frac{1}{n}\sum_{i=1}^{n} \left( Yreal_i - Yestimado_i \right)^2 \]
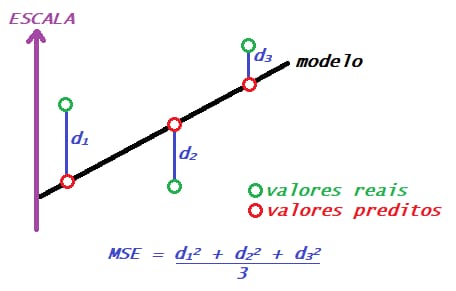
Ex.: O erro quadrático médio para o problema de tempo de erupção do gêiser.
data("faithful")
head(faithful) eruptions waiting
1 3.600 79
2 1.800 54
3 3.333 74
4 2.283 62
5 4.533 85
6 2.883 55# Gráfico do tempo entre as erupções em função do tempo de erupção do gêiseres
plot(faithful$eruptions, faithful$waiting, pch = 20, ylab="Tempo entre Erupções",
xlab = "Tempo de Erupção", main = "Tempo entre as erupções em função do tempo de erupção do gêiser")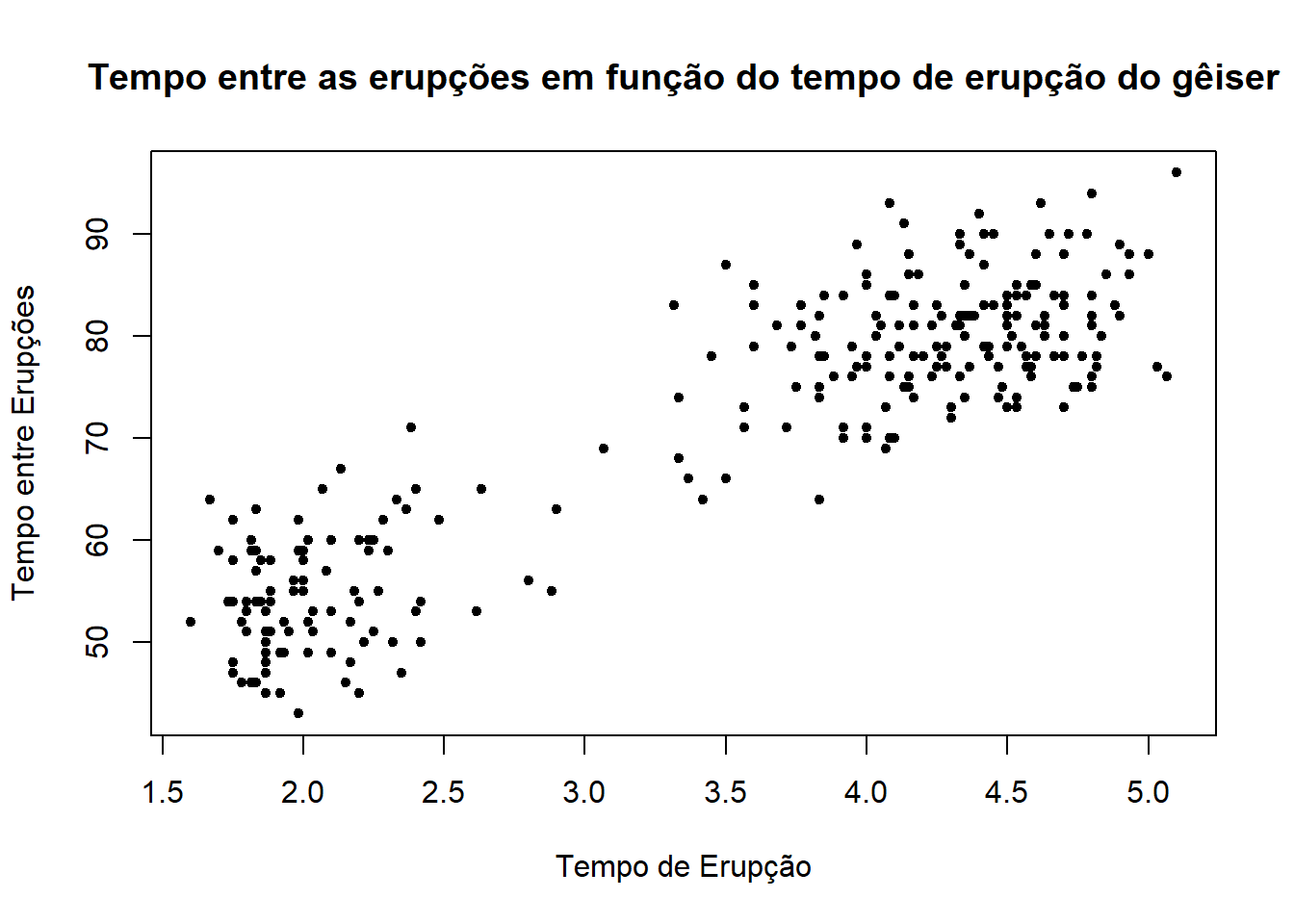
Podemos notar que há uma relação linear positiva entre as variáveis. Vamos então ajustar um modelo de regressão linear.
modelo = lm(faithful$waiting~faithful$eruptions)
plot(y = faithful$waiting, x = faithful$eruptions, pch = 20, ylab="Tempo entre erupções",
xlab = "Tempo de erupção", main = "Tempo entre as erupções em função do tempo de erupção do gêiser")
abline(modelo, col = "red", lwd = 2)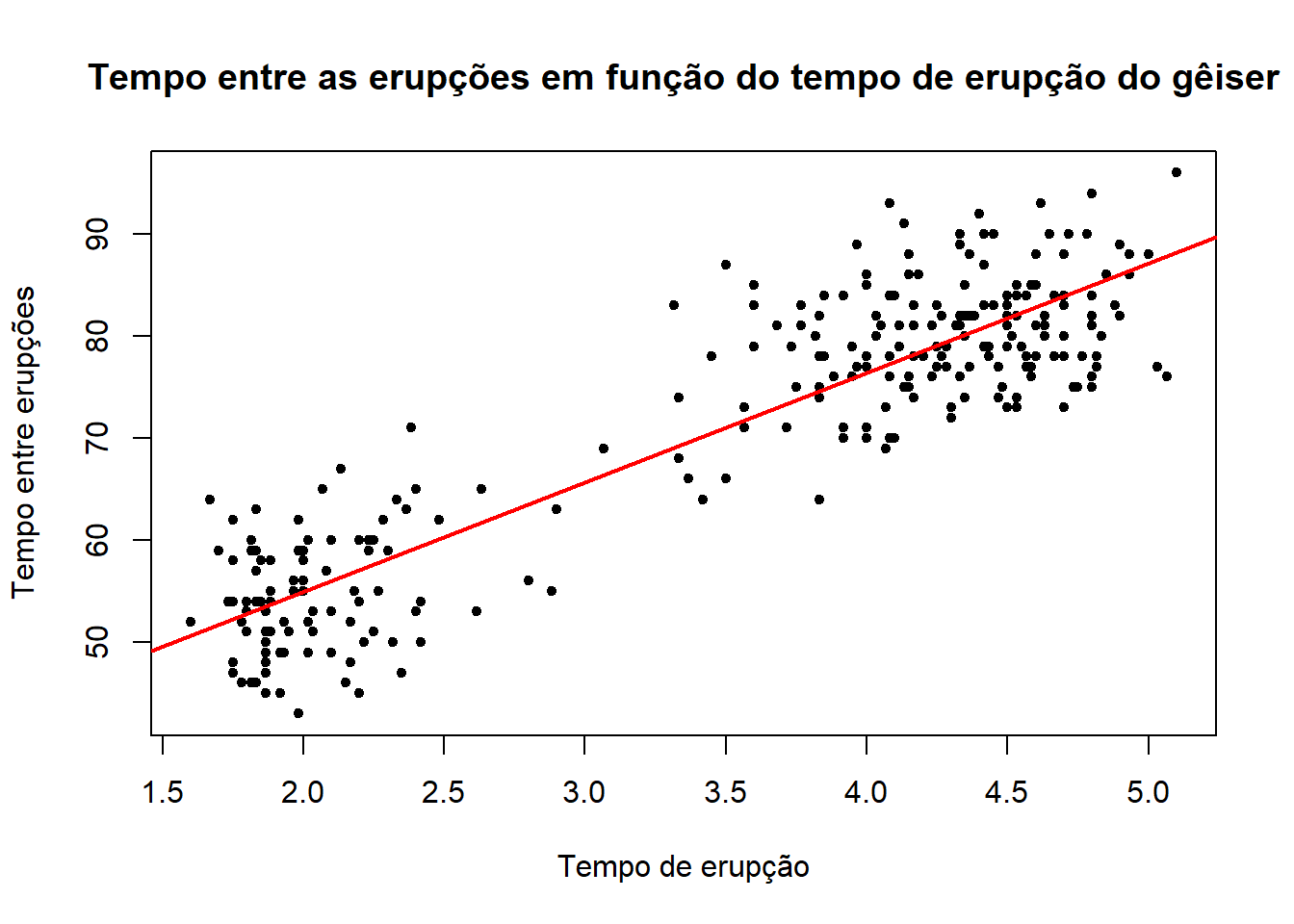
Na reta de regressão temos todos os valores previstos para o tempo de erupção de acordo com os tempos de espera. Podemos então calcular o MSE para o nosso modelo utilizando o comando mse().
mse = sum((teste$waiting-predicao)**2)/nrow(teste)
mse[1] 32.41941Então temos que, em média, o valor estimado para a variável de interesse no conjunto de teste se distancia do valor real observado em 32,41941 escores. Note que esta é uma medida que soma as distâncias ao quadrado, por isso o MSE é um número relativamente grande.